3 Статически неопределимые стержневые системы
3.1 Статически неопределимые стержневые системы
Статически неопределимая стержневая система (рис. 4.7), загружена внешней нагрузкой. Первый стержень нагревается на Δt=100 ºC, а второй — изготовлен короче номинального размера на δ2=0,25 мм.
Требуется:
1 Определить усилия в стержнях, учитывая, что первый стержень стальной (модуль нормальной упругости Е1=2·105 МПа; коэффициент линейного температурного расширения αt=1,52·10-5); а второй — медный (модуль нормальной упругости Е2=105 МПа).
2 Определить напряжения в стержнях и проверить их прочность, принимая допускаемые напряжения: для стального стержня — [σ]=160 МПа, для медного — [σ]=80 МПа.
3 Из условия прочности для наиболее нагруженного стержня определить допускаемую нагрузку [F]. Числовые данные – в таблице 4.1.![Тышкевич, В.Н. Сопротивление материалов. ВолгГТУ Задание 4 Статически неопределимые стержневые системы Статически неопределимая стержневая система (рис. 4.7), загружена внешней нагрузкой. Первый стержень нагревается на Δt=100 ºC, а второй - изготовлен короче номинального размера на δ2=0,25 мм. Требуется: 1 Определить усилия в стержнях, учитывая, что первый стержень стальной (модуль нормальной упругости Е1=2·105 МПа; коэффициент линейного температурного расширения αt=1,52·10-5); а второй - медный (модуль нормальной упругости Е2=105 МПа). 2 Определить напряжения в стержнях и проверить их прочность, принимая допускаемые напряжения: для стального стержня - [σ]=160 МПа, для медного - [σ]=80 МПа. 3 Из условия прочности для наиболее нагруженного стержня определить допускаемую нагрузку [F]. Числовые данные – в таблице 4.1.](https://zadachi24.ru/wp-content/uploads/2017/05/sopromat-3.1.0-287x300.png)
Таблица 4.1 – Исходные данные
| Вариант 39 | |||||||
| Нагрузка | Длина участков и стержней, м | ||||||
| F1, кН | F2, кН | q, кН/м | а | b | c | l1 | l2 |
| — | — | 10 | 4,8 | 2,6 | 1,4 | 1,2 | 1,6 |
Продолжение таблицы 4.1
| Площадь сечения, см2 | Угол, град | ||
| A1 | A2 | α1 | α2 |
| 8 | 8 | 90 | 30 |
ВУЗ: ВолгГТУ
3.2 Определить требуемый размер поперечного сечения стальных стержней (рис.24), удерживающих в равновесии горизонтальный жесткий брус, шарнирно закрепленный одним концом, если [σ]=160 Н/мм². Определив требуемое значение площади А, найти напряжения в поперечных сечениях обоих стержней. Данные своего варианта взять из табл.9.![Определить требуемый размер поперечного сечения стальных стержней (рис.24), удерживающих в равновесии горизонтальный жесткий брус, шарнирно закрепленный одним концом, если [σ]=160 Н/мм². Определив требуемое значение площади А, найти напряжения в поперечных сечениях обоих стержней. Данные своего варианта взять из табл.9.](https://zadachi24.ru/wp-content/uploads/2016/12/sopromat-_3.2.0-300x200.png)
Таблица 9 — Исходные данные
| № задачи и схемы на рис.24 |
Вариант | F, кН | М, кН·м |
| 77,VII | 08 | 8 | 35 |
3.3 Определить требуемый размер поперечного сечения стальных стержней (рис.24), удерживающих в равновесии горизонтальный жесткий брус, шарнирно закрепленный одним концом, если [σ]=160 Н/мм². Определив требуемое значение площади А, найти напряжения в поперечных сечениях обоих стержней. Данные своего варианта взять из табл.9.![Определить требуемый размер поперечного сечения стальных стержней (рис.24), удерживающих в равновесии горизонтальный жесткий брус, шарнирно закрепленный одним концом, если [σ]=160 Н/мм². Определив требуемое значение площади А, найти напряжения в поперечных сечениях обоих стержней. Данные своего варианта взять из табл.9.](https://zadachi24.ru/wp-content/uploads/2016/12/sopromat-_3.3.0-300x191.png)
Таблица 9 — Исходные данные
| № задачи и схемы на рис.24 |
Вариант | F, кН | М, кН·м |
| 72,II | 29 | 20 | 50 |
3.4 Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется:
1) найти усилия и напряжения в стержнях, выразив их через силу F;
2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²).![Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой - 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу F; 2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²).](https://zadachi24.ru/wp-content/uploads/2022/02/sopromat_3.4.1.png)
Данные взять из таблицы 1.
Таблица 1
| Вариант | Данные величины | ||||
| А, см² | а, м | b, м | с, м | Угол α, рад | |
| 1 | 10 | 2,1 | 3,1 | 1,0 | π/4 |
3.5 Расчет статически неопределимой стержневой системы
Определить напряжение в стальных стержнях, поддерживающих абсолютно жёсткую балку. Материал — сталь Ст3, [σ] = 160МПа.![Гаджиев П.И. Махмутов М.М. Сопротивление материалов РГАЗУ Балашиха 2020 Задание 2 Расчет статически неопределимой стержневой системы Определить напряжение в стальных стержнях, поддерживающих абсолютно жёсткую балку. Материал - сталь Ст3, [σ] = 160МПа.](https://zadachi24.ru/wp-content/uploads/2023/05/sopromat_3.5.0-1024x702.png)
Таблица 5 – Исходные данные к заданию 2
| Вариант | А, см² | l, м | F, кН |
| 034 | 10 | 1,3 | 40 |
ВУЗ: РГАЗУ
3.6 (Вариант 213201) Абсолютно жесткий брус опирается на шарнирно-неподвижную опору и прикреплен к двум стальным стержням (рис. 3.3, 3.4).
Требуется:
- Найти усилия и напряжения в стержнях, выразив их через силу F.
- Определить допускаемую нагрузку Fдоп, приравняв наибольшее из напряжений, возникающих в стержнях, расчетному сопротивлению R = 210 МПа .
- Определить предельную нагрузку Fпред, если предел текучести материала стержней σт = 240МПа.
Таблица 3.2
| Схема | А, см² | а, м | b, м | с, м |
| 1 | 12 | 2,1 | 2,1 | 1,3 |
ВУЗ: ТГАСУ
3.7 Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется:
1) найти усилия и напряжения в стержнях, выразив их через силу F;
2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²).
Таблица 1
| Вариант | Данные величины | ||||
| А, см² | а, м | b, м | с, м | Угол α, рад | |
| 1 | 10 | 2,1 | 3,1 | 1,0 | π/4 |
3.8 Абсолютно жесткий брус К шарнирно поддерживается стальными стержнями. Брус нагружен силами Р.
Требуется выполнить проектный расчет (найти площади поперечных сечений стержней), принимая для стальных стержней σпред = σТ. Сила Р = 10 кН, а = 1 м. Запас прочности конструкции принять n = 2,5.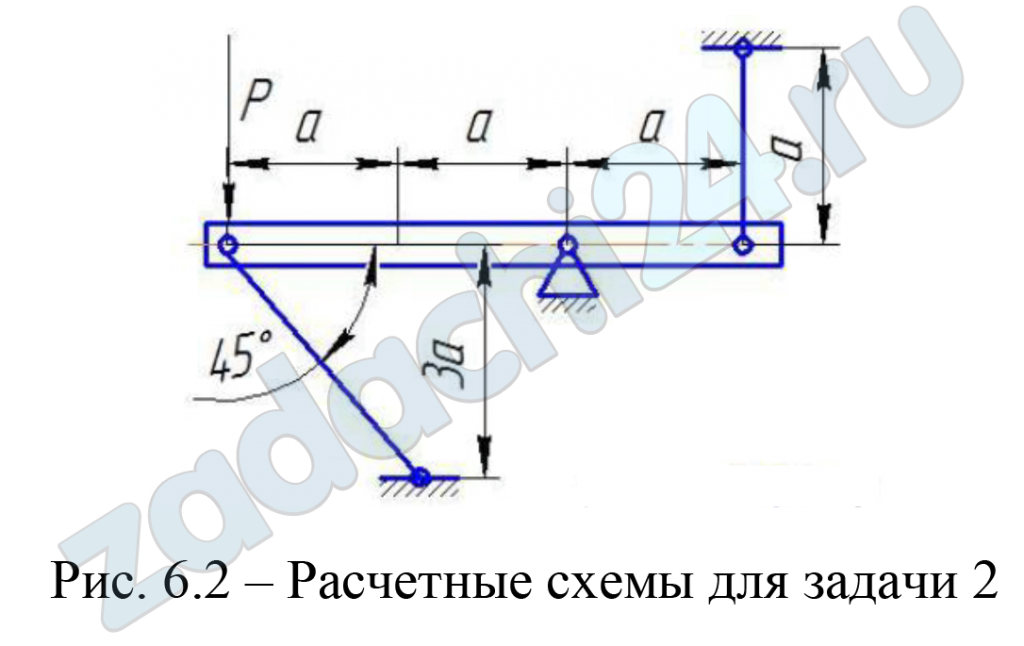
Таблица 2 — Расчетные данные для второй задачи
| № строки | Р | Материал стержня,
сталь марки |
b | c | Предел текучести σТ, МПа |
| 6 | 3Р | 30 | 2а | 3а | 300 |
Все задачи из: Алешин Р.Р. Сопротивление материалов ИВГПУ Иваново 2023
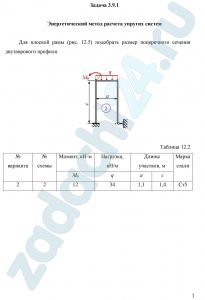
3.9 Энергетический метод расчета упругих систем
Для плоской рамы (рис. 12.5) подобрать размер поперечного сечения двутаврового профиля.
Таблица 12.2
| № варианта | № схемы | Момент, кН·м | Нагрузка, кН/м | Длины участков, м | Марка
стали |
|
| М0 | q | а | c | |||
| 2 | 2 | 12 | 34 | 1,1 | 1,4 | Ст5 |
ВУЗ: ВолгГТУ
3.10 В статически неопределимой шарнирно-стержневой конструкции с абсолютно жестким брусом:
- Определить усилия в стержнях при действии внешней нагрузки, действии температуры на один из стержней и от устранения монтажного зазора в одном из стержней;
- Определить напряжения в стержнях при одновременном действии внешней нагрузки, действии температуры и от устранения монтажного зазора.
- Определить площадь поперечных сечений стержней при заданных воздействиях, в нормальных условиях работы конструкции из расчета на прочность по предельному состоянию.
- По требуемой площади поперечных сечений стержней подобрать двутавровый профиль для изготовления стержней.
Исходные данные.
В расчетах для материала стержней принять:
а) Коэффициент упругости Е = 2·105 МПа;
б) Расчетное сопротивление материала R = 206 МПа;
в) коэффициент линейного расширения α = 12·10-6 (1/ºС).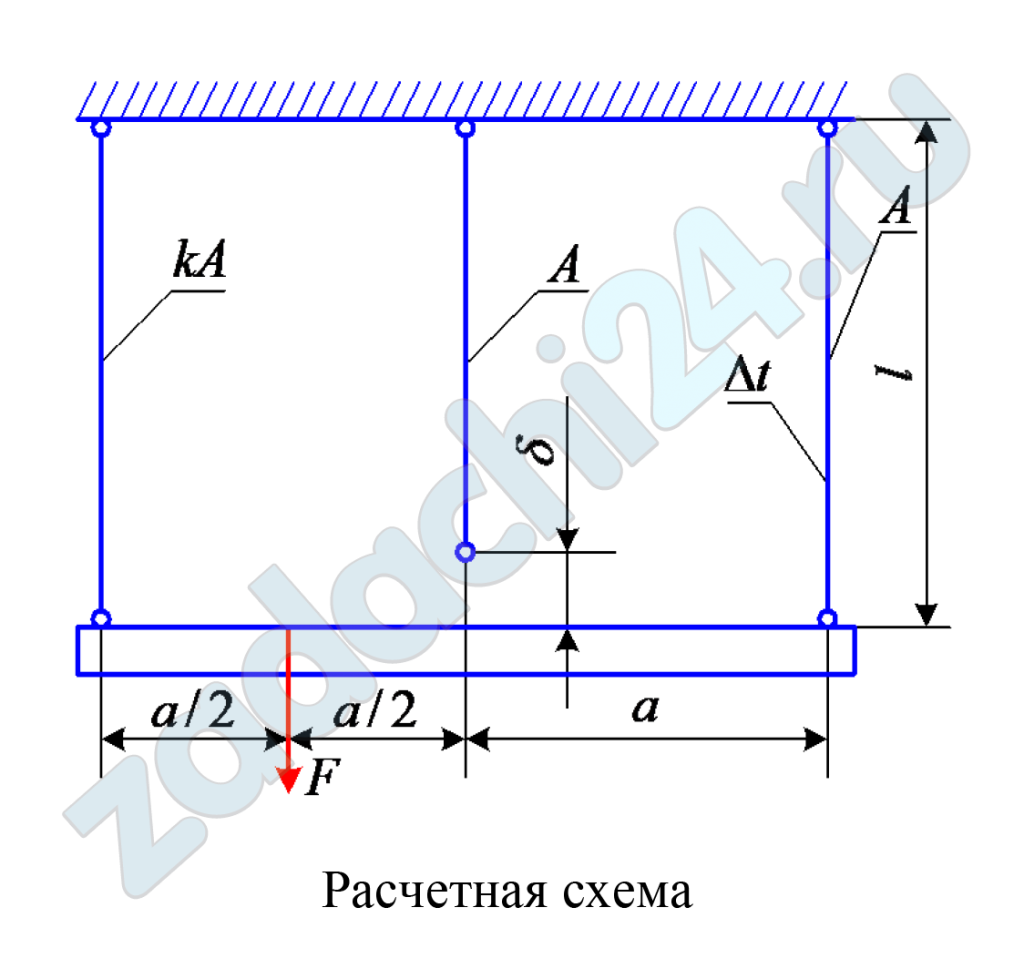
ИСХОДНЫЕ ДАННЫЕ
| № варианта | l, м | l1, м | а, м | К | F, МН | Δt, ºС | δ, 10-4 м |
| 21 | 2,4 | — | 1,1 | 2 | 0,4 | -20 | 4,0 |
Оформление готовой работы

![Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу F; 2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²)](https://zadachi24.ru/wp-content/uploads/2022/02/sopromat_3.4.1_page_1-205x300.jpg)
![Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу F; 2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²)](https://zadachi24.ru/wp-content/uploads/2022/02/sopromat_3.4.1_page_2-205x300.jpg)
![Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу F; 2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²)](https://zadachi24.ru/wp-content/uploads/2022/02/sopromat_3.4.1_page_3-205x300.jpg)
![Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу F; 2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²)](https://zadachi24.ru/wp-content/uploads/2022/02/sopromat_3.4.1_page_4-205x300.jpg)









![Абсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой - 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу F; 2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²).](https://zadachi24.ru/wp-content/uploads/2024/03/sopromat_3.7.1-1024x725.png)
![бсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу F; 2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²).](https://zadachi24.ru/wp-content/uploads/2024/03/sopromat_3.7.1_page_1-205x300.jpg)
![бсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу F; 2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²).](https://zadachi24.ru/wp-content/uploads/2024/03/sopromat_3.7.1_page_2-205x300.jpg)
![бсолютно жесткий горизонтально расположенный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров (рис. 1). Один стержень имеет поперечное сечение А, другой — 2А. На брус действует вертикальная сила F, приложенная в указанной на рисунке точке. Требуется: 1) найти усилия и напряжения в стержнях, выразив их через силу F; 2) найти допускаемую нагрузку Fдоп, приравняв большее из напряжений в двух стержнях допускаемому напряжению [σ] = 160 МПа,(16 кН/см²).](https://zadachi24.ru/wp-content/uploads/2024/03/sopromat_3.7.1_page_3-205x300.jpg)