1 Растяжение и сжатие
1.1 Конструкция состоит из двух стержней, соединенных между собой и с основанием шарнирами (рис.1). К шарнирному болту С привязан груз Р. Требуется определить внутренние усилия в стержнях и подобрать их сечение по допускаемым напряжениям на сжатие и растяжение. Величина силы Р, форма сечения и допускаемые напряжения приведены в табл.1. 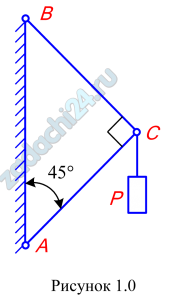
Таблица 1
| Вариант 4 | |||
| Сечение стержней | Величина Р, кН | [σ]С, МПа | [σ]Р, МПа |
 |
10 | 160 | 100 |
1.2 (Вариант 29) Двухступенчатый стальной брус, длины ступеней которого указаны на рис.23 (схемы I-X) нагружены силами F1 и F2. Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить удлинение (укорочение) бруса, приняв Е=2·105 МПа. Числовые значения сил F1 и F2, а также площадей поперечных сечений ступеней A1 и A2 для своего варианта взять из табл.8.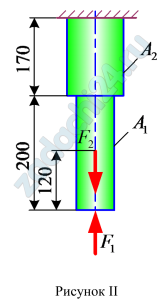
Таблица 8 — Исходные данные
| № задачи и схемы на рис.23 |
F1, кН | F2, кН | А1, см2 | А2, см2 |
| 62,II | 4,8 | 10,0 | 0,4 | 0,8 |
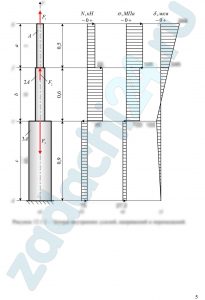
1.3 (Вариант 2396) Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки F и при найденном значении нагрузки вычислить наибольшее перемещение бруса, а также максимальное удлинение участка a.
Принять А=200 мм², l=200 мм, s=2, остальные данные взять из табл.3.1 и табл.3.2.![Для консольного бруса переменного сечения (рис.3.1) построить эпюры нормальной силы, нормальных напряжений и продольных перемещений. Определить из условия прочности допустимое значение нагрузки F и при найденном значении нагрузки вычислить наибольшее перемещение бруса, а также максимальное удлинение участка a. Принять А=200 мм², l=200 мм, s=2, остальные данные взять из табл.3.1 и табл.3.2. Таблица 3.1 - Исходные данные [table “3467” not found /]<br />
Таблица 3.2 - Механические характеристики материала [table “3468” not found /]<br />
Дано: схема бруса (рис.3.1) А1=1,7А; b=2l; F1=-2F; c=l; F2=-4F; Материал - Магниевый сплав МА-5; a=2l; F3=2F; А=200 мм²; l=200 мм; s=2.](https://zadachi24.ru/wp-content/uploads/2016/12/sopromat_1.3.0-300x125.png)
Таблица 3.1 — Исходные данные
| A1/A | b/l | F1/F | c/l | F2/F | Материал | № схемы | a/l | F3/F |
| 1,70 | 2,0 | -2 | 1,0 | -4 | Магн. спл. МА — 5 |
1 | 2,0 | 2,0 |
Таблица 3.2 — Механические характеристики материала
| 1 Пластичные материалы | ||||||
| Материал | Марка | σт, МПа | σв, МПа | τт, МПа | Е·10-5 МПа. | μ |
| Магниевый сплав |
МА-5 | 220 | 300 | 160 | 0,72 | 0,27 |
Дано: схема бруса (рис.3.1) А1=1,7А; b=2l; F1=-2F; c=l; F2=-4F; Материал — Магниевый сплав МА-5; a=2l; F3=2F; А=200 мм²; l=200 мм; s=2.
Из табл.3.2 находим σт=220 МПа; Е=0,72·105 МПа.
Скачать файл (оплата в RUB)1.4 Стальной ступенчатый брус нагружен сосредоточенными силами. Соотношение между площадями поперечных сечений приведены на рис. 12.1. Из условия прочности при растяжении найти площадь поперечного сечения А. Определить удлинение стержня.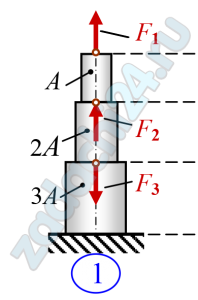
Таблица 12.2
| № варианта 1 | |||||||
| № схемы | Силы, кН | Длины участков, м | Марка
стали |
||||
| F1 | F2 | F3 | а | b | c | ||
| 1 | 23 | 22 | 60 | 0,5 | 0,6 | 0,9 | Ст3 |
Варианты задачи: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30.
ВУЗ: ВолгГТУ
1.5 Расчеты на прочность и жесткость при растяжении (сжатии)
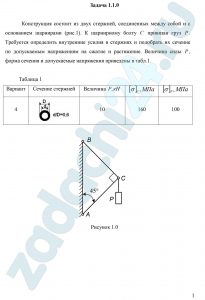
Ступенчатый стержень находится под действием продольных сил F, приложенных по концам или в центре соответствующего участка стержня. Материал стержня – сталь с допускаемым напряжением [σ]=200 МПа, модуль продольной упругости Е=2·105 МПа.
Требуется:
1 Построить эпюры: продольных усилий, напряжений, перемещений;
2 Проверить прочность стержня.![Тышкевич, В. Н. Сопротивление материалов Задание 3 Расчеты на прочность и жесткость при растяжении (сжатии) Ступенчатый стержень находится под действием продольных сил F, приложенных по концам или в центре соответствующего участка стержня. Материал стержня – сталь с допускаемым напряжением [σ]=200 МПа, модуль продольной упругости Е=2·105 МПа. Требуется: 1 Построить эпюры: продольных усилий, напряжений, перемещений; 2 Проверить прочность стержня.](https://zadachi24.ru/wp-content/uploads/2017/01/sopromat-1.5.0-260x300.png)
Таблица 3.1 – Исходные данные
| Вариант 39 | |||||
| Длина участка, см | Площадь поперечного сечения, см2 | ||||
| l1 | l2 | l3 | A1 | A2 | A3 |
| 60 | 30 | 48 | 10 | 4 | 8 |
Продолжение таблицы 3.1
| Нагрузка, кН | |||||
| F1 | F2 | F3 | F4 | F5 | F6 |
| 140 | 80 | — | 100 | — | — |
ВУЗ: ВолгГТУ
1.6 Построение эпюр при растяжении (сжатии)
Стальной двухступенчатый брус, длины ступеней которого указаны на рисунке 1, нагружен силами F1, F2, F3 (положение точек приложения сил задано размерами). Построить эпюры продольных сил и нормальных напряжений по длине бруса, а также эпюру перемещений поперечных сечений бруса. Определить перемещение Δl свободного конца бруса, приняв Е=2·105 МПа. Числовые значения сил F1, F2, F3, а также площади поперечных сечений ступеней A1 и A2 для своего варианта взять из таблицы 1.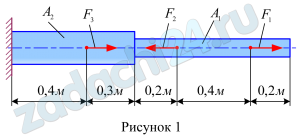
Таблица 1
| Вариант | F1 | F2 | F3 | A1 | A2 |
| кН | см2 | ||||
| 3 | 24 | 11 | 27 | 1,5 | 4,0 |
1.7 (Вариант 165456) Стальной стержень (Е=2·105 МПа) находится под действием продольной силы Р. Постройте эпюры продольных сил N, напряжений σ, перемещений Δ. Проверьте прочность стержня. Данные взять из табл. П.2.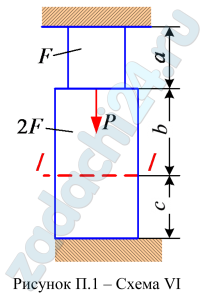
Таблица П.2
| Схема по рис. П1, П2, П3, П4 | F, см2 | a | b | c | Р·102, Н |
| м | |||||
| VI | 15 | 2,4 | 2,5 | 1,6 | 1400 |
Варианты задачи: 131519, 186891.
Скачать файл (оплата в RUB)Все задачи из: Костенко Н.А. Сопротивление материалов Москва 2004
1.8 Растяжение-сжатие прямого бруса
Дан брус, нагруженный, как показано на рисунке 1. Цифровые данные – в таблице 2.
Требуется:
1. Определить реакцию в заделке (если требуется).
2. Составить выражения для продольных сил на каждом участке бруса.
3. Определить значений продольных сил на границе каждого участка.
4. Рассчитать нормальные напряжения на границе каждого участка.
5. Вычислить абсолютную деформацию каждого участка, а также перемещения всех граничных сечений. При необходимости определить экстремальные значения перемещений.
6. Построить эпюры
— продольных сил;
— нормальных напряжений;
Таблица 2
| №№ п.п. | l, м | P1, кН | q1, кН/м | А1, мм2 | Е·10-5, МПа |
| 4 | 0,50 | 25 | 68 | 95 | 1,95 |
Принять: P2=1,25P1; P3=1,4P1; A2=0,85A1; A3=0,75A1; q2=1,1q1.
Скачать файл (оплата в RUB)Все задачи из: Бирфельд А.А. Сопротивление материалов РГАТА
1.9 Тема «Растяжение – сжатие»
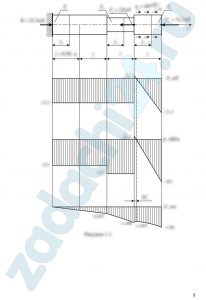
Произвести расчет стержня постоянного сечения (рис. 1) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σ]=210 МПа и модулем Юнга Е=2,1·105 МПа. Требуется:
1) вычислить продольные силы на участках стержня и построить эпюру продольных сил N по его длине;
2) определить размеры поперечного сечения (сторону квадрата или диаметр);
3) вычислить нормальные напряжения на участках стержня и построить эпюру нормальных напряжений σ по его длине;
4) вычислить деформации участков стержня и построить эпюру перемещений δ.
Исходные цифровые данные приведены в табл. 1. ![Лехов О.С. и др. Теоретическая и прикладная механика Екатеринбург РГППУ 2012 Задача 4 Тема «Растяжение – сжатие» Произвести расчет стержня постоянного сечения (рис. 1) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σ]=210 МПа и модулем Юнга Е=2,1·105 МПа. Требуется: 1) вычислить продольные силы на участках стержня и построить эпюру продольных сил N по его длине; 2) определить размеры поперечного сечения (сторону квадрата или диаметр); 3) вычислить нормальные напряжения на участках стержня и построить эпюру нормальных напряжений σ по его длине; 4) вычислить деформации участков стержня и построить эпюру перемещений δ. Исходные цифровые данные приведены в табл. 1.](https://zadachi24.ru/wp-content/uploads/2019/05/sopromat_1.9.0-300x157.png)
Таблица 1
| Вариант 531 | |||
| l1, м | l2, м | l3, м | l4, м |
| 0,9 | 0,8 | 1,5 | 0,9 |
Продолжение таблицы 1
| F1, МН | F2, МН | F3, МН | Номер схемы (рис. 1) |
Форма сечения |
| 1,4 | 0,4 | 1,7 | 1 | Квадрат |
ВУЗ: РГППУ
1.10 (Вариант 6) Практическая работа на растяжение и сжатие
Цель: Научиться строить эпюры продольных сил Nz и нормальных напряжений σ и производить проверочный расчет.
Задача. Двухступенчатый брус в соответствии с рисунком нагружен силами Р1=15 кН; Р2=10 кН; Р3=5 кН и площадями поперечных сечений А1=1,2 см²; А2=2,0 см².
а) построить эпюры продольных сил Nz и нормальных напряжений σ;
б) проверить условие прочности, если [σ]=160 МПа;
в) определить удлинение (укорочение) бруса Δl, если а=0,2 м, b=0,4 м, с=0,5 м, Е=2·105 МПа.![Практическая работа на растяжение и сжатие Цель: Научиться строить эпюры продольных сил Nz и нормальных напряжений σ и производить проверочный расчет. Задача. Двухступенчатый брус в соответствии с рисунком нагружен силами Р1=15 кН; Р2=10 кН; Р3=5 кН и площадями поперечных сечений А1=1,2 см²; А2=2,0 см². а) построить эпюры продольных сил Nz и нормальных напряжений σ; б) проверить условие прочности, если [σ]=160 МПа; в) определить удлинение (укорочение) бруса Δl, если а=0,2 м, b=0,4 м, с=0,5 м, Е=2·105 МПа.](https://zadachi24.ru/wp-content/uploads/2019/05/sopromat_1.10.0-300x129.png)