Мустафаев Ю.К. Червинский В.П. Теоретическая механика СамГУПС Самара 2020
12.3 Применение принципа Даламбера к определению реакций связи
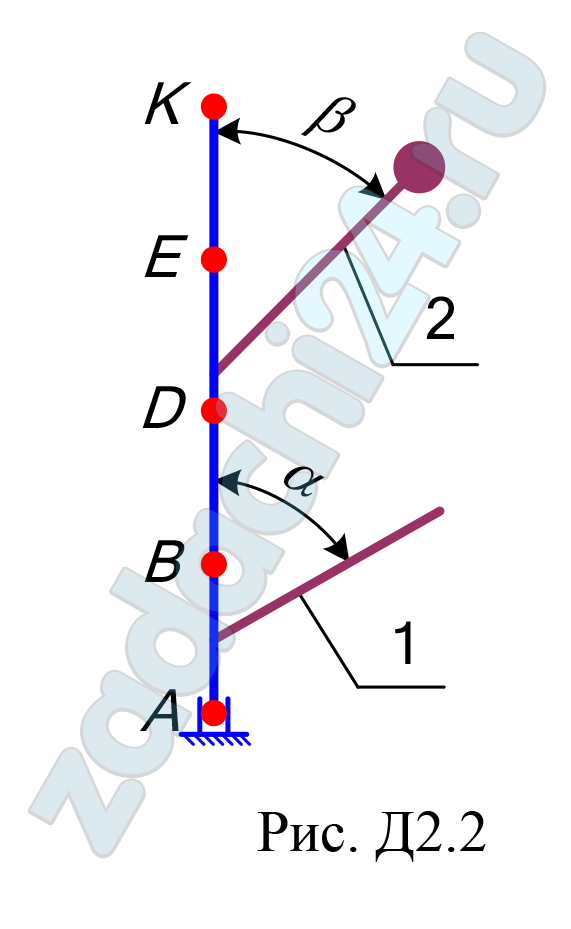
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.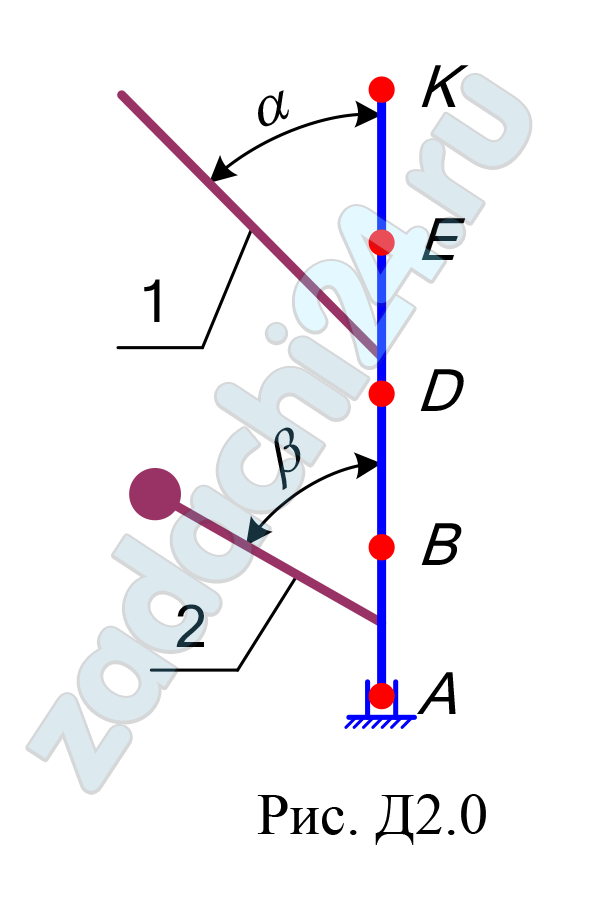
Таблица Д2
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
12.4 Применение принципа Даламбера к определению реакций связи
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.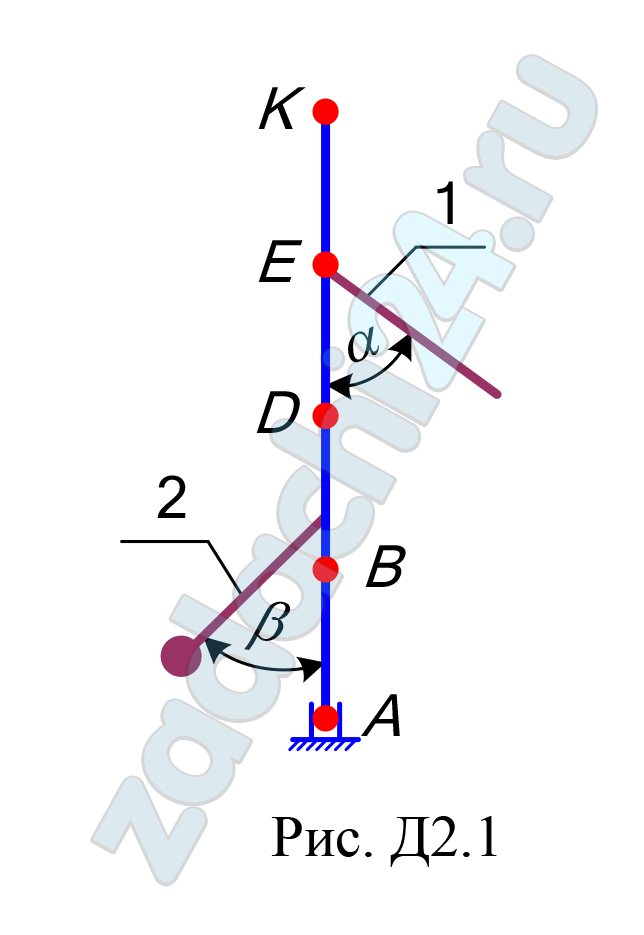
Таблица Д2
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
12.5 Применение принципа Даламбера к определению реакций связи
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
12.6 Применение принципа Даламбера к определению реакций связи
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.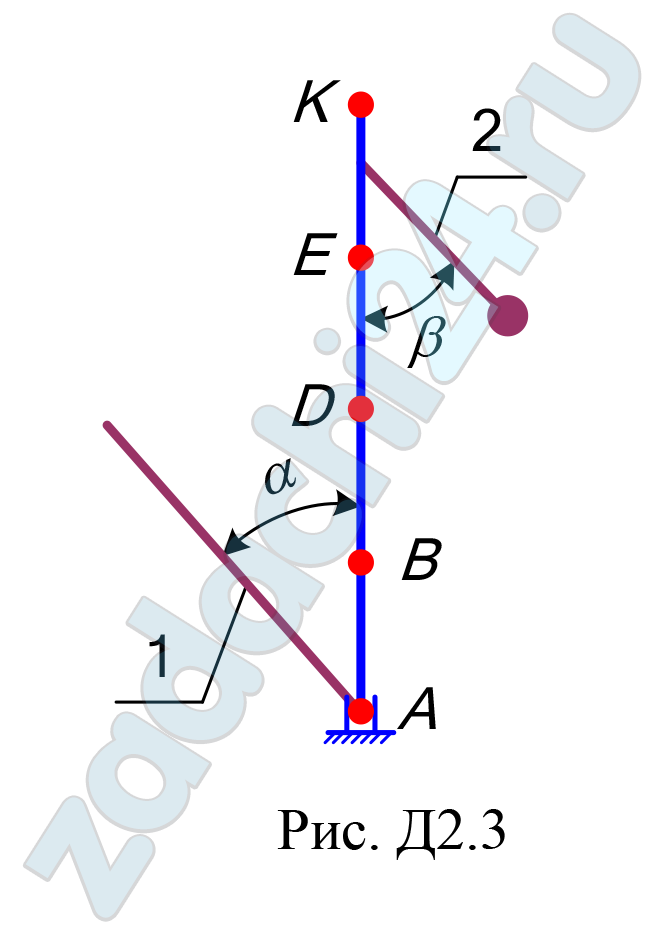
Таблица Д2
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
12.7 Применение принципа Даламбера к определению реакций связи
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.
Таблица Д2
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
12.8 Применение принципа Даламбера к определению реакций связи
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.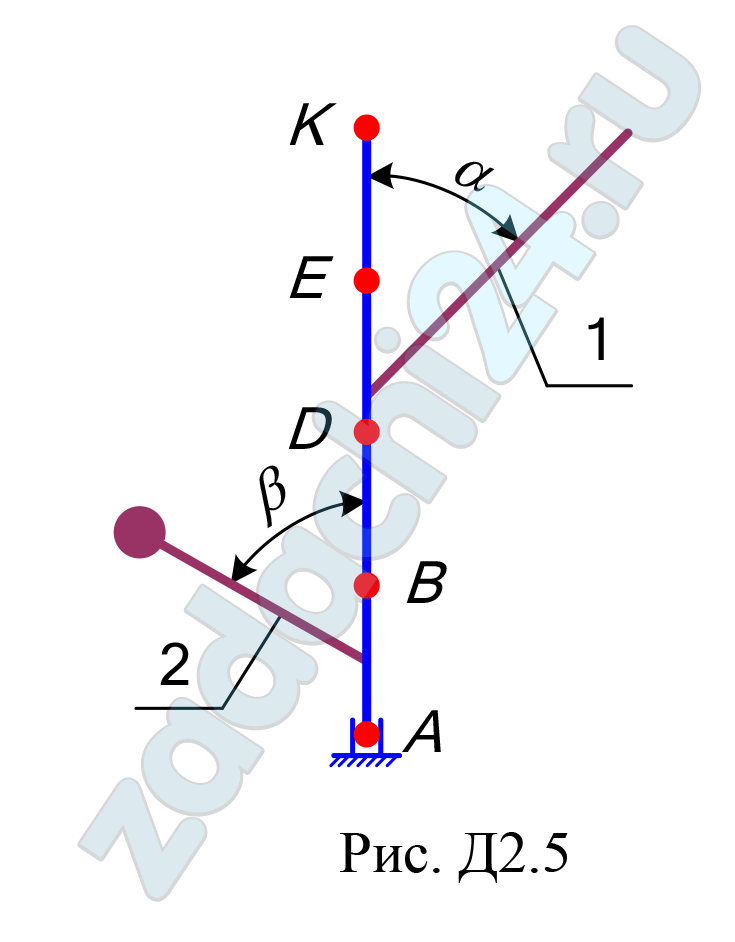
Таблица Д2
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
12.9 Применение принципа Даламбера к определению реакций связи
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.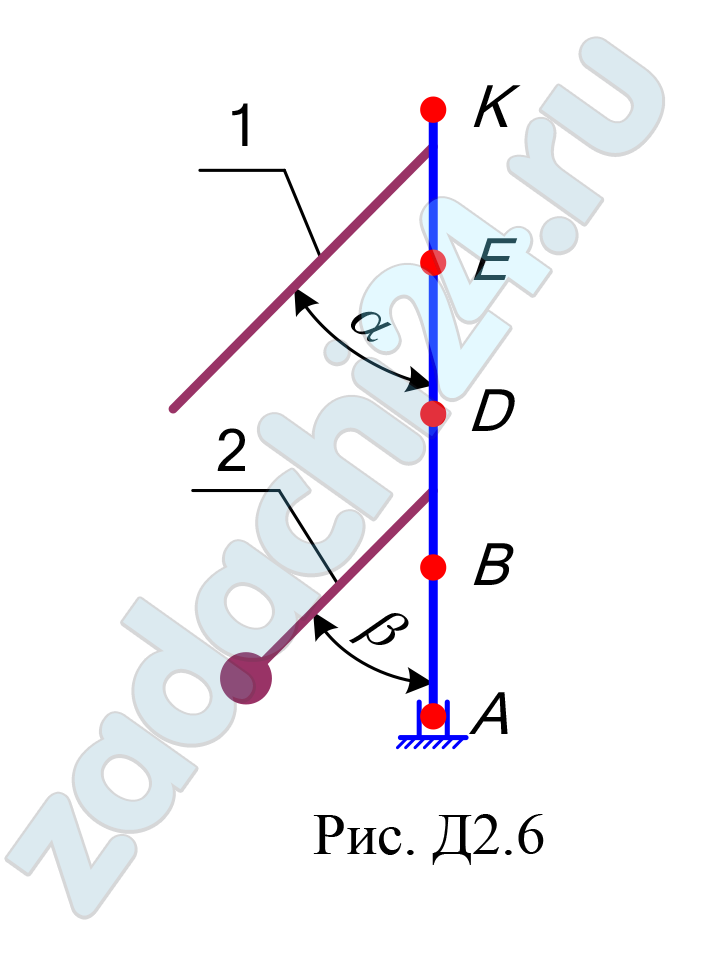
Таблица Д2
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
12.10 Применение принципа Даламбера к определению реакций связи
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.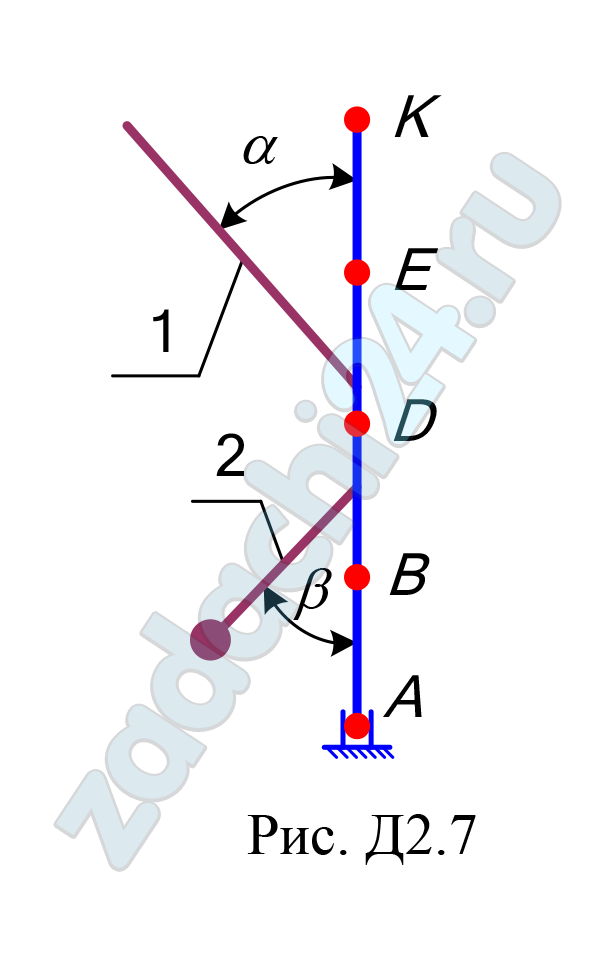
Таблица Д2
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
12.11 Применение принципа Даламбера к определению реакций связи
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.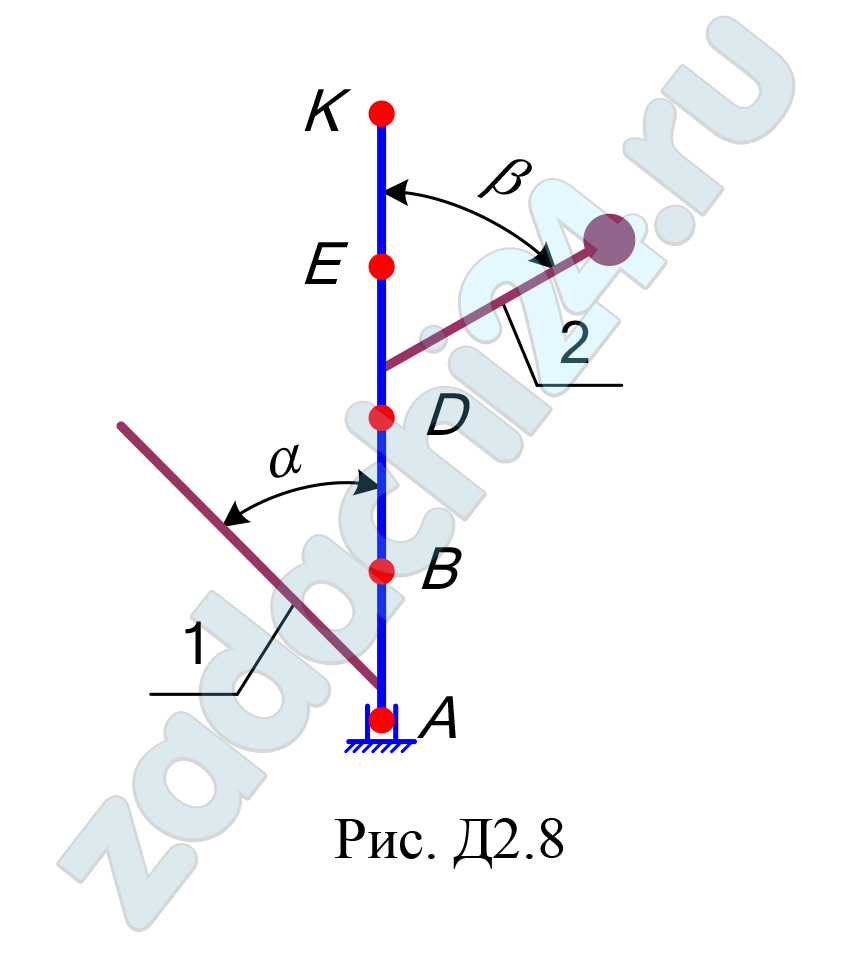
Таблица Д2
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
12.12 Применение принципа Даламбера к определению реакций связи
Вертикальный вал АК (рис. Д2.0–Д2.9), вращающийся с постоянной угловой скоростью ω = 10 c-1, закреплен подпятником в точке А и цилиндрическим подшипником в точке, указанной в таблице Д2, в столбце 2. При этом АВ = ВD = DЕ = ЕК = а. К валу жестко прикреплены однородный стержень 1 длиной l = 0,6 м, имеющий массу m1 =3 кг, и невесомый стержень 2 длиной l2 = 0,4 м и с точечной массой m2 = 5 кг на конце. Оба стержня лежат в одной плоскости. Точки крепления стержней к валу указаны в таблице в столбцах 3 и 4, а углы α и β – в столбцах 5 и 6.
Пренебрегая весом вала, определить реакции подпятника и подшипника. При подсчетах принять a = 0,4 м.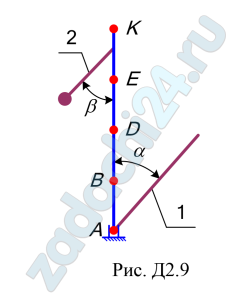
Таблица Д2
| Номер
условия |
Подшипник
в точке |
Крепление | α, град | β, град | |
| Стержень 1
в точке |
Стержень 2
в точке |
||||
| 0 | D | B | K | 45 | 30 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС