11 Динамика материальной системы

11.1 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.Применение теоремы об изменении кинетической энергии к исследованию движения механической системы Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2. Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3. Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4+4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf

11.2 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.Применение теоремы об изменении кинетической энергии к исследованию движения механической системы Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2. Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3. Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4+4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf

11.3 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.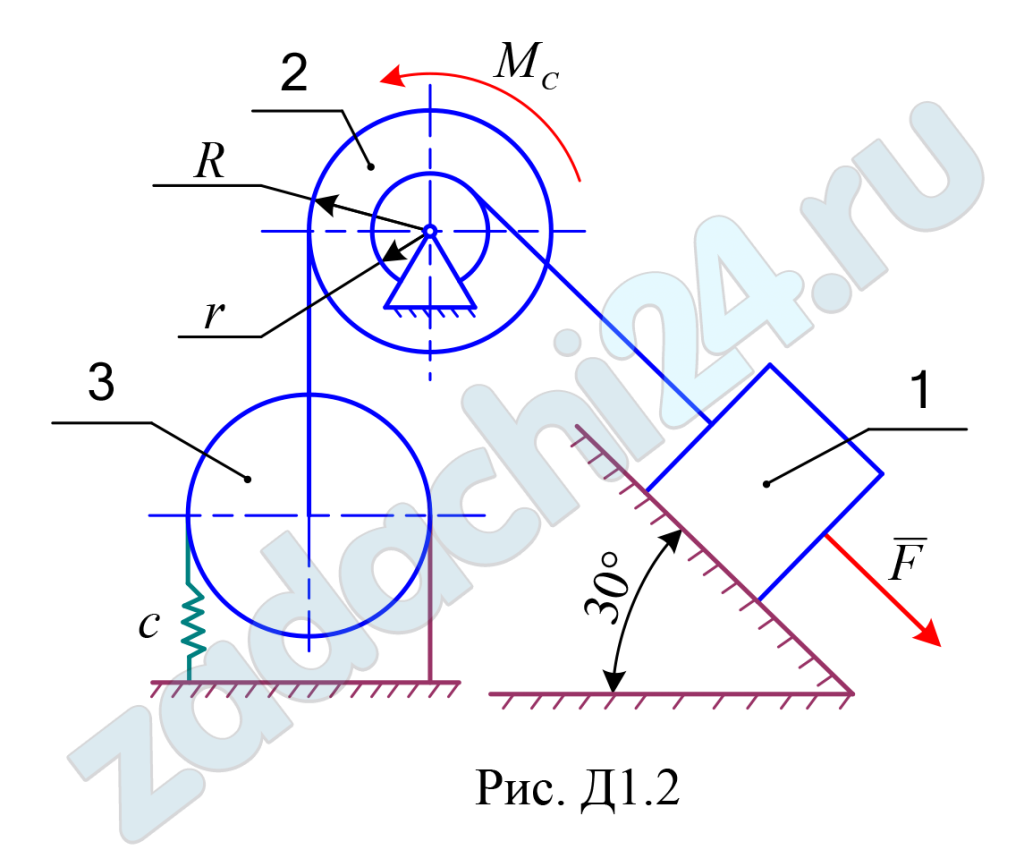Применение теоремы об изменении кинетической энергии к исследованию движения механической системы Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2. Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3. Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4 + 4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf

11.4 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.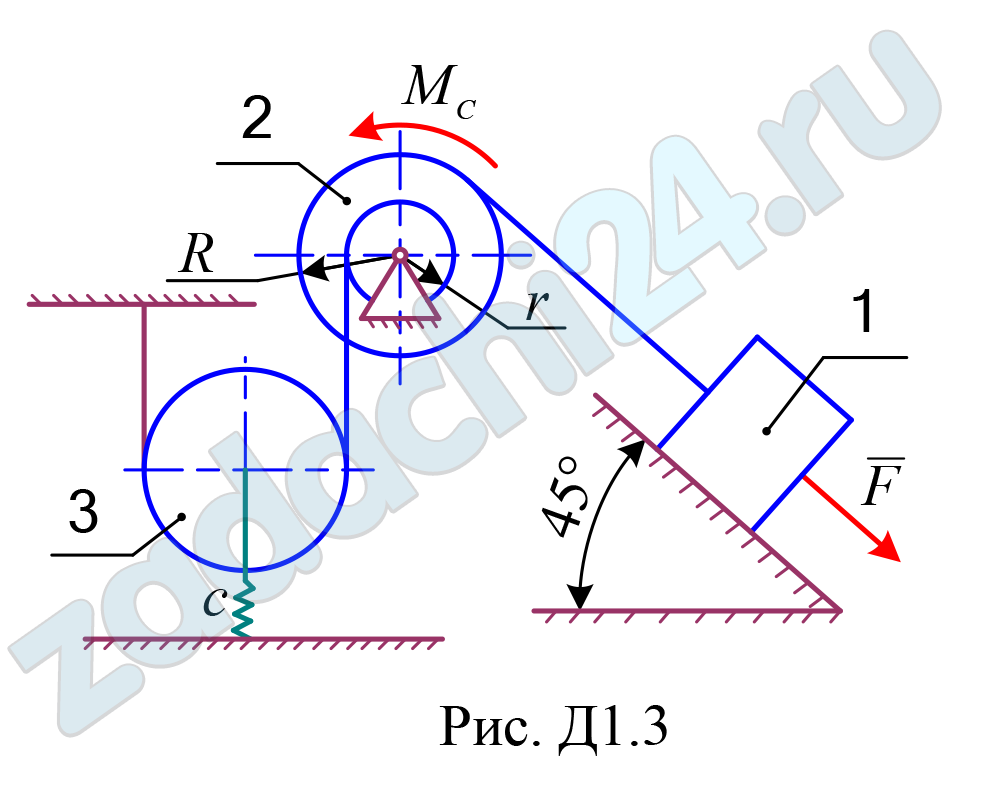Применение теоремы об изменении кинетической энергии к исследованию движения механической системы Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2. Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3. Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4 + 4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf

11.5 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.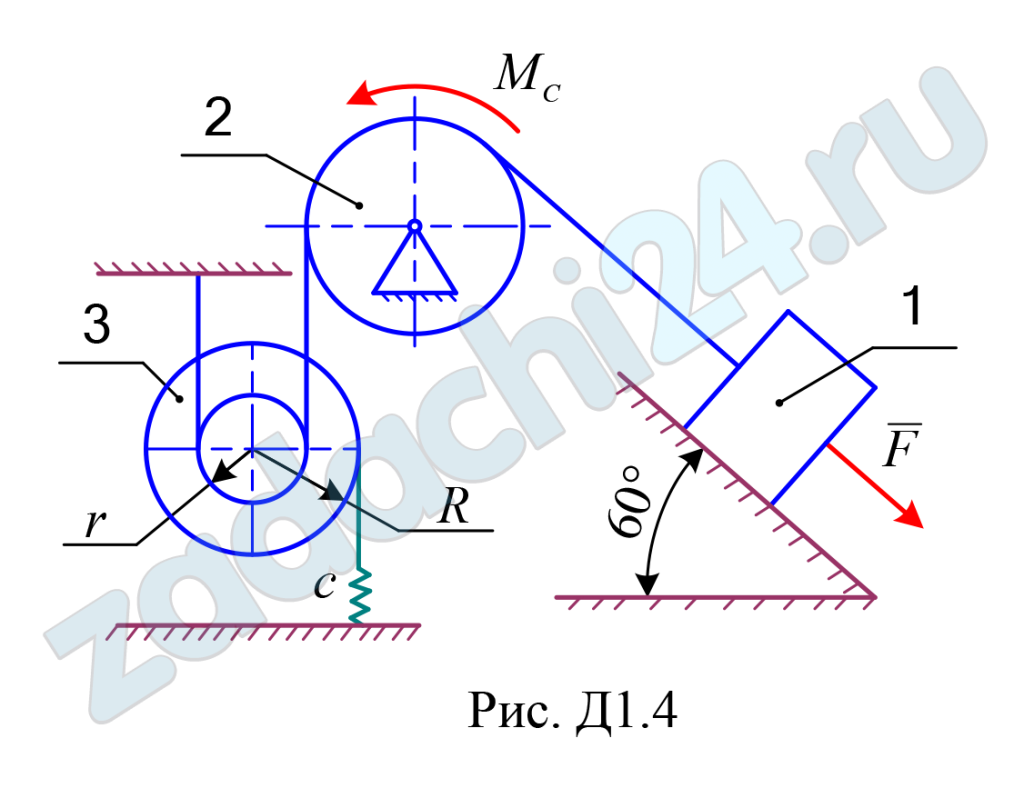Применение теоремы об изменении кинетической энергии к исследованию движения механической системы Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2. Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3. Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4 + 4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf

11.6 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4 + 4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf

11.7 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.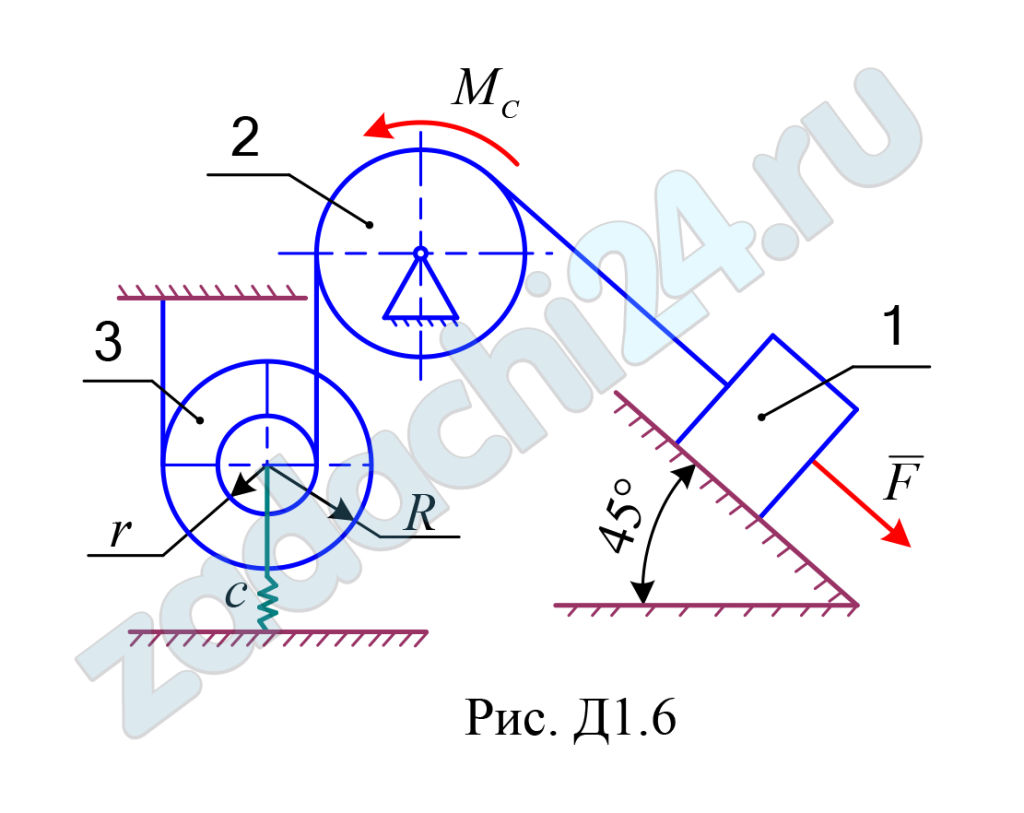Применение теоремы об изменении кинетической энергии к исследованию движения механической системы Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2. Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3. Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4 + 4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf

11.8 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.Применение теоремы об изменении кинетической энергии к исследованию движения механической системы Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2. Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3. Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4 + 4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf

11.9 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.Применение теоремы об изменении кинетической энергии к исследованию движения механической системы Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2. Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3. Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4 + 4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf

11.10 Применение теоремы об изменении кинетической энергии к исследованию движения механической системы

Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2.

Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3.

Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения. Данные для численных расчётов приведены в таблице Д1.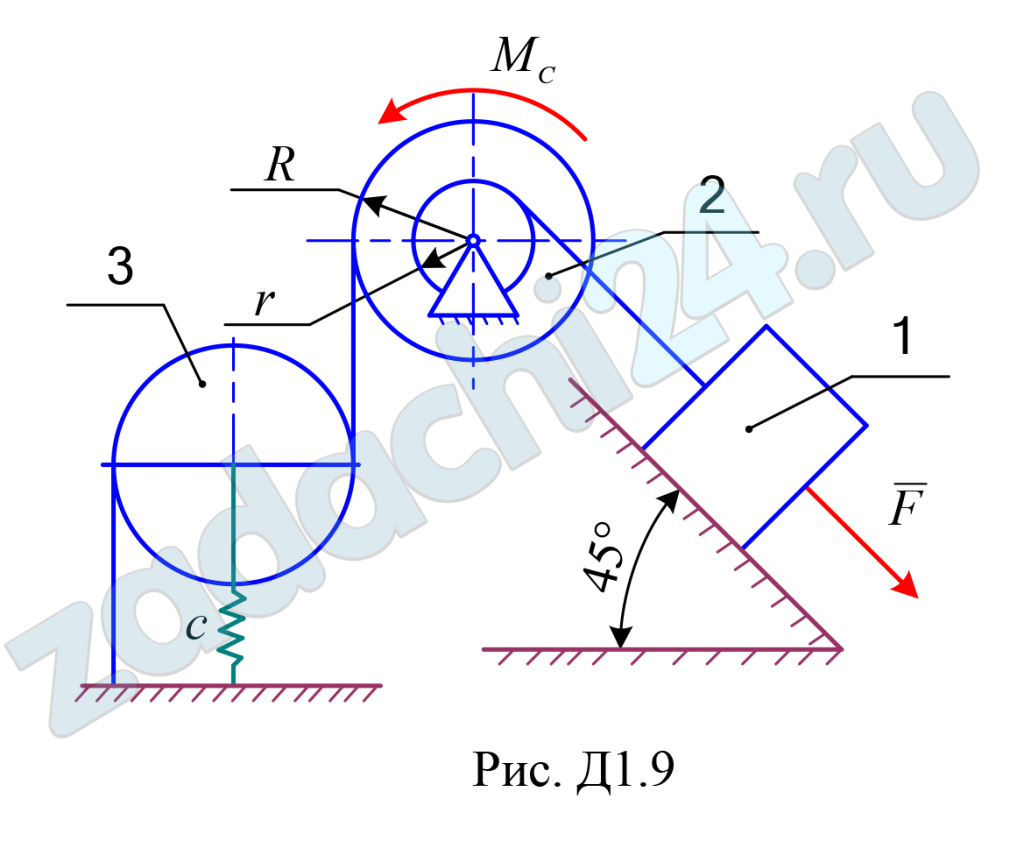Применение теоремы об изменении кинетической энергии к исследованию движения механической системы Механическая система состоит из трёх движущихся тел (рис. Д1.0 –Д1.9), соединенных нерастяжимыми нитями, параллельными соответствующим плоскостям. Неподвижные и подвижные блоки одного радиуса считать однородными сплошными цилиндрами радиуса R; ступенчатые блоки (подвижные и неподвижные) с радиусами ступеней R и r имеют радиус инерции ρ. К одному из тел прикреплена пружина жёсткости c. Под действием силы F = F(s), зависящей от перемещения s точки её приложения, система приходит в движение из состояния покоя; деформация пружины в начальный момент времени равна нулю. При движении на шкив 2 действует момент сил сопротивления MC = MC(φ), зависящий от угла φ поворота шкива 2. Определить значение искомой величины в момент времени, когда центр масс тела 1 переместиться на заданную величину s1. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υC3 – скорости груза 1 и скорость центра масс катка 3 соответственно; ω2, ω3 и – угловые скорости тел 2 и 3. Все катки, включая катки, обмотанные нитями, движутся по плоскостям без скольжения.

Таблица Д1

Номер

условия

 m1, кг m2, кг m3, кг с, Н/м MC(φ), Н·м
0 6 5 4 150 0,5 φ

Продолжение таблицы Д1

F = F(s), Н ρ, м s1, м R, м r, м Найти
80(4 + 4s) 0,15 0,1 0,4 0,2 υC3
В корзину – 250 RUB

Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Методические указания.pdf