6 Прямой изгиб

6.21 (Вариант 22092) Для стальной балки, нагруженной в соответствии с расчетной схемой, из условия прочности по нормальным напряжениям подобрать размеры поперечного сечения.

Расчет выполнить для четырех вариантов поперечного сечения:

– двутавр;

– прямоугольное с соотношением сторон ;

– круглое сплошное с внешним диаметром D;

– кольцевое с соотношением диаметров .

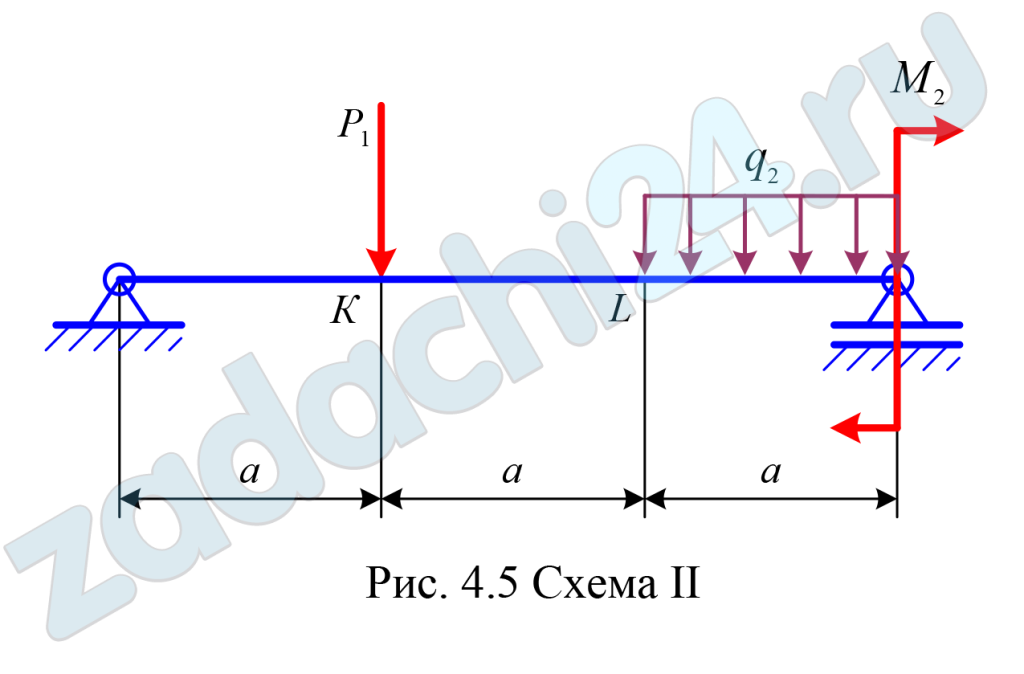
Выбрать наиболее рациональное поперечное сечение и для него построить эпюры нормальных и касательных напряжений в опасных поперечных сечениях балки. Исходные данные для расчета принять по табл. 4.1 и рис. 4.5, полагая: Р = qa; m = Pa = qa² ; q = 10 кН/м; а = 1 м.

Для стальной балки, нагруженной в соответствии с расчетной схемой, из условия прочности по нормальным напряжениям подобрать размеры поперечного сечения. Расчет выполнить для четырех вариантов поперечного сечения: – двутавр; – прямоугольное с соотношением сторон ; – круглое сплошное с внешним диаметром D; – кольцевое с соотношением диаметров . Выбрать наиболее рациональное поперечное сечение и для него построить эпюры нормальных и касательных напряжений в опасных поперечных сечениях балки. Исходные данные для расчета принять по табл. 4.1 и рис. 4.5, полагая: Р = qa; m = Pa = qa² ; q = 10 кН/м; а = 1 м.Таблица 4.1

Внешние нагрузки
m1 m2 Р1 Р2 q1 q2
2m m Р Р q q

Продолжение таблицы 4.1

Материал балки
Сталь Чугун
Марка Предел

текучести σт, МПа

 Марка Предел прочности, МПа
при растяжении σвр при сжатии σвс
40ХН 900 СЧ25 280 1000

Коэффициент запаса прочности принять nт =1,5; допускаемые касательные напряжения принять [τ] = 0,6[σ].

В корзину – 500 RUB

ВУЗ: ПГУ

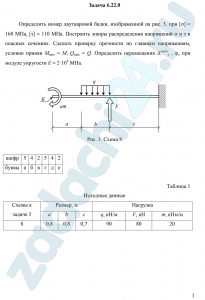
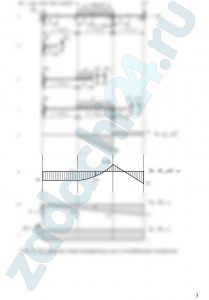
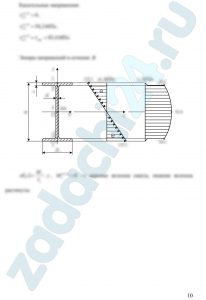
6.22 (Вариант 542) Определить номер двутавровой балки, изображенной на рис. 3, при [σ] = 160 МПа, [τ] = 110 МПа. Построить эпюры распределения напряжений σ и τ в опасных сечениях. Сделать проверку прочности по главным напряжениям, условно приняв Мmax = М, Qmax = Q. Определить перемещения Δвертк , φк при модуле упругости Е = 2·105 МПа.Определить номер двутавровой балки, изображенной на рис. 3, при [σ] = 160 МПа, [τ] = 110 МПа. Построить эпюры распределения напряжений σ и τ в опасных сечениях. Сделать проверку прочности по главным напряжениям, условно приняв Мmax = М, Qmax = Q. Определить перемещения Δвертк , φк при модуле упругости Е = 2·105 МПа.

Таблица 1

Исходные данные

Схемы к

задаче 3

 Размер, м Нагрузка
a b c q, кН/м F, кН m, кНм/м
8 0,8 0,8 0,7 90 80 20
В корзину – 600 RUB

Методические указания.pdf

ВУЗ: ДВГУПС

6.23 Для заданной схемы балки (рис. 3) требуется построить эпюру поперечных сил и эпюру изгибающих моментов, найти максимальный изгибающий момент Ммакс и по нему подобрать стальную двутавровую балку с указанием ее номера по ГОСТ 8239-72.

Допускаемое напряжение на изгиб принимать [σ] = 150 МПа.(15 кН/см²). Данные для расчета взять из таблицы 3.

Некоторые значения моментов сопротивления сечения при изгибе Wx для балок двутаврового сечения (ГОСТ 8239-72) приведены (табл.3).Для заданной схемы балки (рис. 3) требуется построить эпюру поперечных сил и эпюру изгибающих моментов, найти максимальный изгибающий момент Ммакс и по нему подобрать стальную двутавровую балку с указанием ее номера по ГОСТ 8239-72. Допускаемое напряжение на изгиб принимать [σ] = 150 МПа.(15 кН/см²). Данные для расчета взять из таблицы 3. Некоторые значения моментов сопротивления сечения при изгибе Wx для балок двутаврового сечения (ГОСТ 8239-72) приведены (табл.3).

Таблица 3

Вариант 1
а, м b, м с, м l, м Изгибающий

момент М, кН·м

 Сосредоточенная

сила F, кН

 Равномерно

распределяемая

нагрузка q, кН/м
2,0 3,2 1,8 10 7 20 22
В корзину – 300 RUB

6.24 (Вариант 07_53069) Полная проверка на прочность двутавровой балки

Для заданной стальной балки из условия прочности подобрать номер двутавра по ГОСТ 8239-89 и произвести полную проверку на прочность.

Схемы балок приведены на рис. 5, численные значения даны в табл. 5.

Допускаемые напряжения для Ст.3: [σ] = 160 МПа, [τ] = 95 МПа.Полная проверка на прочность двутавровой балки Для заданной стальной балки из условия прочности подобрать номер двутавра по ГОСТ 8239-89 и произвести полную проверку на прочность. Схемы балок приведены на рис. 5, численные значения даны в табл. 5. Допускаемые напряжения для Ст.3: [σ] = 160 МПа, [τ] = 95 МПа.

Таблица 5

Номер схемы l, м а, м b, м F, кН q, кН/м М, кН·м
7 2,4 0,40 0,45 210 56 24
В корзину – 650 RUB
Оформление готовой работы

6.25 (Вариант 7) Для заданного типа стержня (рис.2. 0-9) требуется написать выражение F и М для каждого участка в общем виде, построить эпюры поперечных сил и изгибающих моментов, найти максимальный момент и подобрать стандартный профиль любого вида сечения из алюминия или стали. Данные взять из табл. 2. Длины отрезков даны в метрах.Для заданного типа стержня (рис.2. 0-9) требуется написать выражение F и М для каждого участка в общем виде, построить эпюры поперечных сил и изгибающих моментов, найти максимальный момент и подобрать стандартный профиль любого вида сечения из алюминия или стали. Данные взять из табл. 2. Длины отрезков даны в метрах.

Таблица 2 — Данные величины

а, м b, м с, м l, м
0,34 0,46 0,25 1,3

Продолжение таблицы 2

Изгибающий момент, М, Н·м Сосредоточенная
сила, F, Н		 Равномерно
распределяемая
нагрузка, q, Н/м
100 120 150
В корзину – 150 RUB

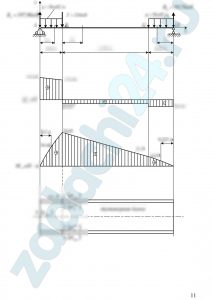
6.26 Для заданных двух систем балок (рис. 3.1) требуется написать выражения Q и М для каждого участка в общем виде, построить эпюры Q и М, найти максимальное М и подобрать:

1) для схемы а деревянную балку круглого поперечного сечения при [σ] = 80 МПа;

2) для схемы б стальную балку двутаврового поперечного сечения при [σ] = 160 МПа.

Данные взять из табл. 3.1.Для заданных двух систем балок (рис. 3.1) требуется написать выражения Q и М для каждого участка в общем виде, построить эпюры Q и М, найти максимальное М и подобрать: 1) для схемы а деревянную балку круглого поперечного сечения при [σ] = 80 МПа; 2) для схемы б стальную балку двутаврового поперечного сечения при [σ] = 160 МПа.

Таблица 3.1

Номер

строки

 l a М, кН·м Р, кН q, кН/м
м
5 2 1 10 50 20
В корзину – 550 RUB
Оформление готовой работы