4 Силы давления жидкости на криволинейные стенки
4.71 Построить тело давления и определить величину и направление силы гидростатического давления жидкости, относительная плотность которой δ=1,25, на затвор (рис.4.17). Затвор является частью цилиндра радиусом R=1,2 м и шириной b=4,5 м. Глубина воды Н=2,0 м.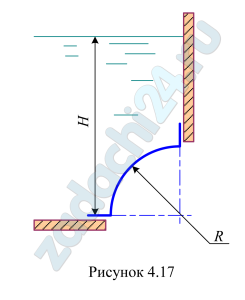
4.72 Цилиндрический резервуар диаметром D, заполненный бензином плотностью ρбенз=750 кг/м³, закрыт полусферической крышкой, закрепленной шестью болтами (рис. 3.27). Резервуар находится под давлением. Показание манометра на глубине h от оси крышки равно рман.
Определить величину и направление растягивающей силы, воспринимаемой болтами, соответствующие вертикальной силе давления на полусферическую крышку. Рассчитать горизонтальные силы, разрывающие полусферическую крышку по сечению 1-1, показать расстояние линий действия этих сил от оси полусферы.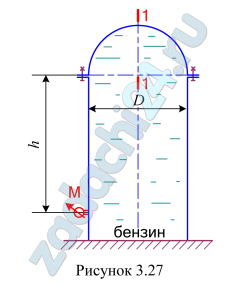
Таблица 1 – Исходные данные
| Вариант | D, м | h, м | рман, ат |
| а | 1,2 | 1,9 | 0,24 |
4.73 Определить величину, угол наклона и глубину центра давления для равнодействующей давления воды на криволинейную стенку АВ (рис. 3.11) длиной L=10 м. Действующий напор Н=4,0 м. Криволинейная стенка представляет часть цилиндрической поверхности с секторным углом φ=60º.
Ответ: равнодействующая сила давления воды R=1012 кН, угол наклона силы к горизонту α=39º; глубина центра давления yDравн=2,91 м.
Скачать файл (банки РФ) 200 RUBУчебник: Часс С.И. Гидромеханика в примерах и задачах УГГУ 2006.pdf
ВУЗ: УГГУ
Все задачи из: Часс С.И. Гидромеханика в примерах и задачах УГГУ 2006
4.74 Определить вертикальную и горизонтальную составляющие силы давления воды, действующие на коническую крышку (рис. 4.34), если избыточное давление в резервуаре р0и=0,7·105 Па, d=1,2 м, Н=3,0 м, l=1,0 м.
4.75 Построить тело давления, определить силу давления жидкости, которая отрывает полусферическую крышку резервуара от основания (рис. 4.27), и угол ее наклона к горизонту α при следующих данных: радиус сферы R=1,6 м, относительная плотность жидкости δ=0,9, манометрическое давление рм=8 кПа.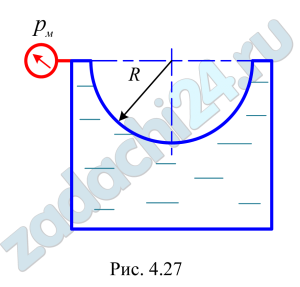
4.76 Построить тело давления и определить силу давления жидкости Р на полусферическую крышку (рис. 4.33) при следующих данных: глубина жидкости Н=2,0 м, радиус сферы R=1,6 м, плотность жидкости ρ=950 кг/м³, избыточное давление р0и=18 кПа.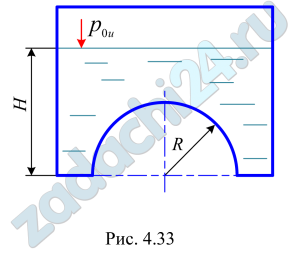
4.77 Определить величину, линию действия, глубину центра давления hD и угол наклона к горизонту равнодействующей давления воды на секторный затвор ACB с центральным углом φ=90º (рис. 3.15).
Для выпуска воды затвор поворачивается относительно оси O-O. Удерживаемые напоры h и H, длина затвора L. Плотность воды ρ=10³ кг/м³.
При решении задачи криволинейную поверхность АСВ представить в масштабе, секторный затвор в виде сечения вертикальной плоскостью.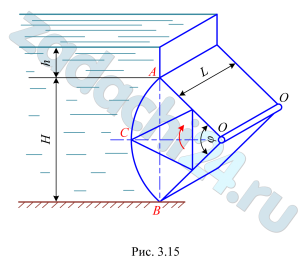
Таблица 1 – Исходные данные
| Вариант | h, м | Н, м | L, м |
| а | 0,5 | 2,0 | 5,0 |
ВУЗ: УГГУ
4.78 Определить величину и направление силы давления воды на боковую поверхность цилиндрического затвора диаметром d=1,6 м и длиной l=4,0 м (рис. 4.40), если Н1=3,0 м, Н2=d/2.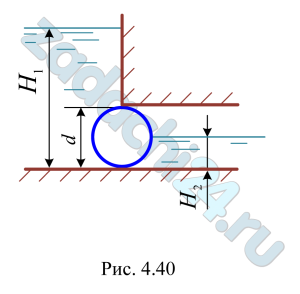
4.79 В вертикальной стенки резервуара сделано прямоугольное отверстие для выпуска воды. Отверстие перекрывается цилиндрическим затвором диаметром d и длиной L, установленным на цапфах (рис. 3.11). Действующий напор на уровне оси затвора H.
Определить величину, линию действия, геометрическое положение и угол наклона к горизонту равнодействующей давления на поверхность затвора ACB.
Таблица 1 – Исходные данные
| Вариант | Н, м | d, м | L, м |
| а | 0,8 | 0,6 | 2,0 |
ВУЗ: УГГУ
4.80 Определить горизонтальную и вертикальную составляющие силы гидростатического давления нефти плотностью ρ=850 кг/м³ на выпуклую торцовую стенку, если D=3,5 м, Н=2,1 м, а объем выпуклой части (на рис. 4.36 заштрихован) V=1,5 м³, избыточное давление в резервуаре р0и=0,05·105 Па.
















