4 Силы давления жидкости на криволинейные стенки
4.181 Построить тело давления и определить силу давления жидкости Р на полусферическую крышку и угол ее наклона к горизонту α (рис. 4.51) при следующих данных: радиус сферы R = 0,6 м, относительная плотность жидкости δ = 0,7 . Вакуумметрическое давление в резервуаре р0в = 0,2·105 Па.
4.182 Построить тело давления и определить силу давления жидкости на цилиндрическую поверхность резервуара (рис. 4.51) и угол ее наклона к горизонту α при следующих данных: радиус образующей цилиндра R = 2,4 м, длина образующей цилиндра b = 1,5 м, относительная плотность жидкости δ = 1,26. Вакуумметрическое давление в резервуаре р0в = 0,45 ·105 Па.
4.183 Построить тело давления и определить силу давления жидкости Р, действующую на полусферическую крышку, и угол ее наклона к горизонту α (рис. 4.52) при следующих данных: радиус образующей сферы R = 1,8 м, плотность жидкости ρ = 750 кг/м³. Вакуумметрическое давление в резервуаре р0в = 0,4·105 Па.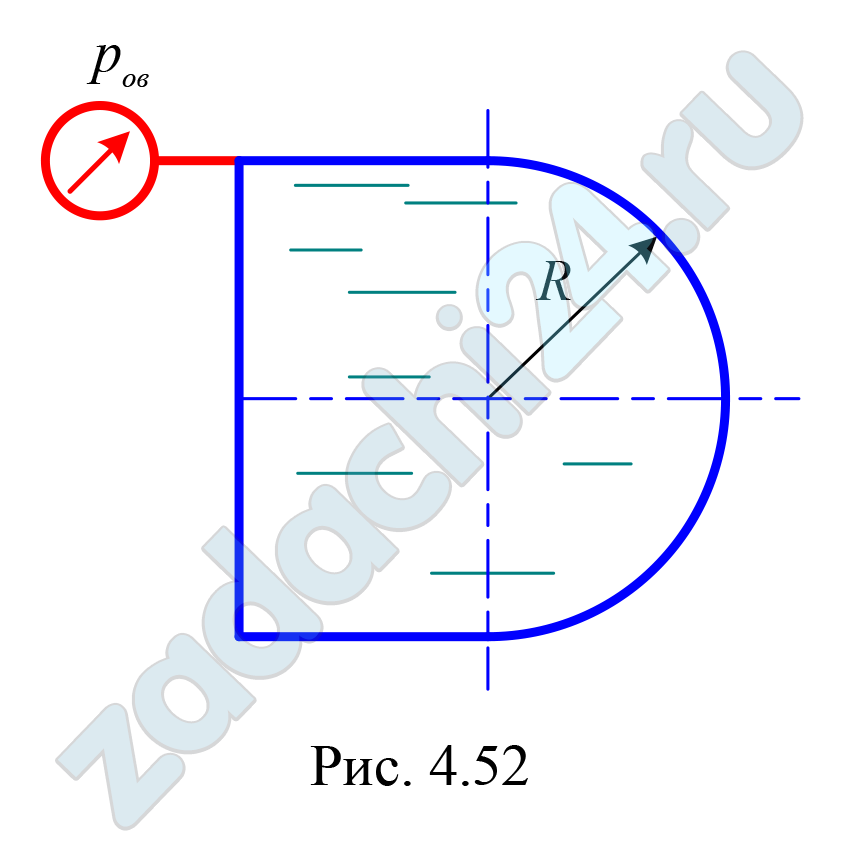
4.184 Построить тело давления и определить силу давления жидкости на цилиндрическую поверхность резервуара (рис. 4.52) и угол ее наклона к горизонту α при следующих данных: радиус образующей цилиндра R = 1,5 м, длина образующей цилиндра b = 0,8 м, относительная плотность жидкости δ = 0,95. Вакуумметрическое давление в резервуаре р0в = 0,35·105 Па.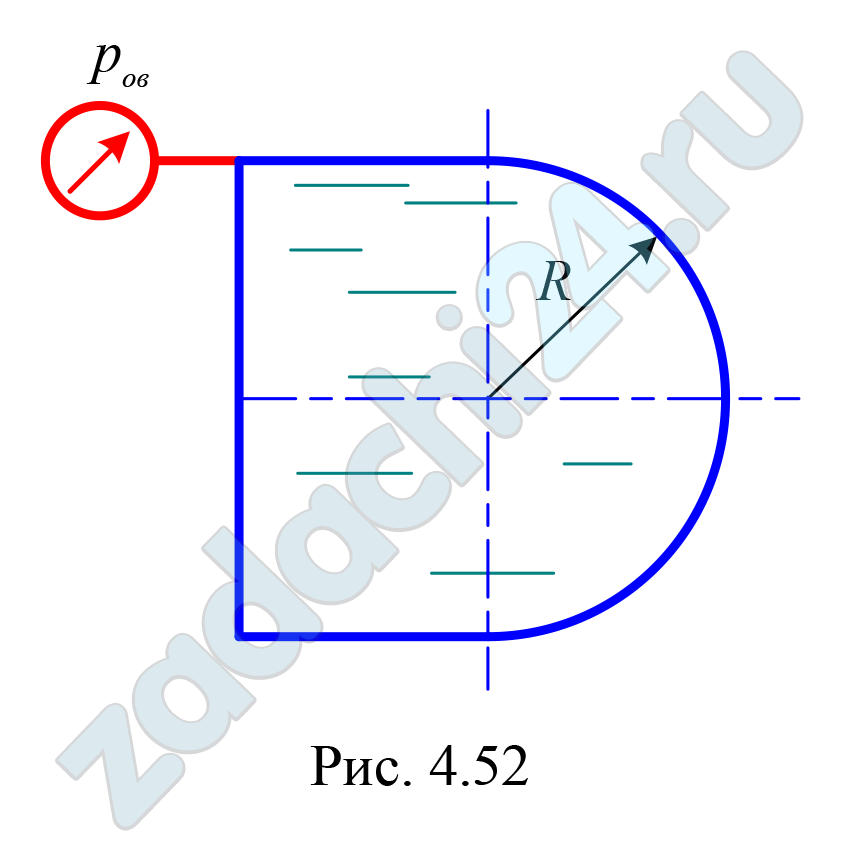
4.185 Резервуар, донная часть которого имеет полусферу, наполнен водой (рис. 4.53). Построить тело давления и определить силу давления воды на полусферу, если радиус сферы R = 1,4 м, глубина жидкости в резервуаре Н = 2,5 м, вакуумметрическое давление в резервуаре р0в = 0,28·105 Па.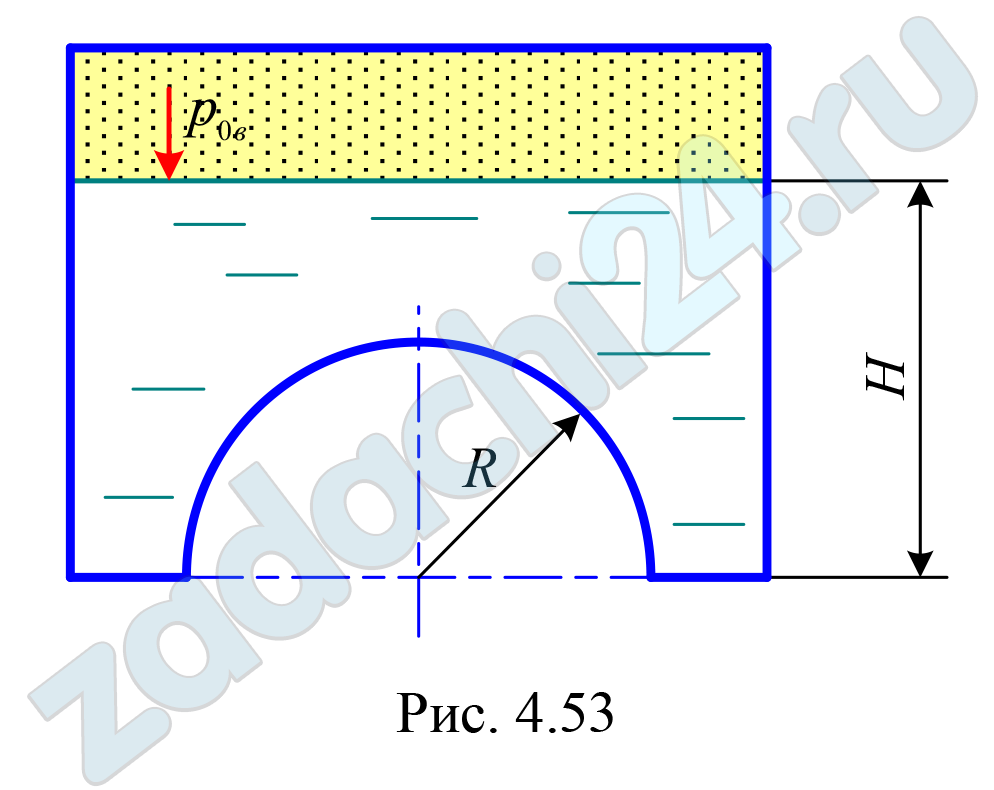
4.186 Построить тело давления и определить силу давления жидкости Р, действующую на цилиндрическую поверхность, и угол ее наклона к горизонту α (рис. 4.54) при следующих данных: радиус образующей цилиндра R = 1,2 м, длина образующей цилиндра В = 1,5 м, плотность жидкости ρ = 850 кг/м³, вакуумметрическое давление р0в = 22 кПа.
4.187 Определить усилие, отрывающее боковую поверхность от дна резервуара (рис. 4.57), заполненного нефтепродуктами (ρн = 870 кг/м³) при следующих данных: Н = 3 м, d = 1 м, D = 2 м, р0и = 0,1·105 Па.
4.188 Определить силу давления нефти на цилиндрическую поверхность АВ, а также положение центра давления, если глубина жидкости в резервуаре равна h, длина поверхности в плоскости, перпендикулярной плоскости чертежа, l, радиус закругления – r. Плотность нефти ρн = 900 кг/м³.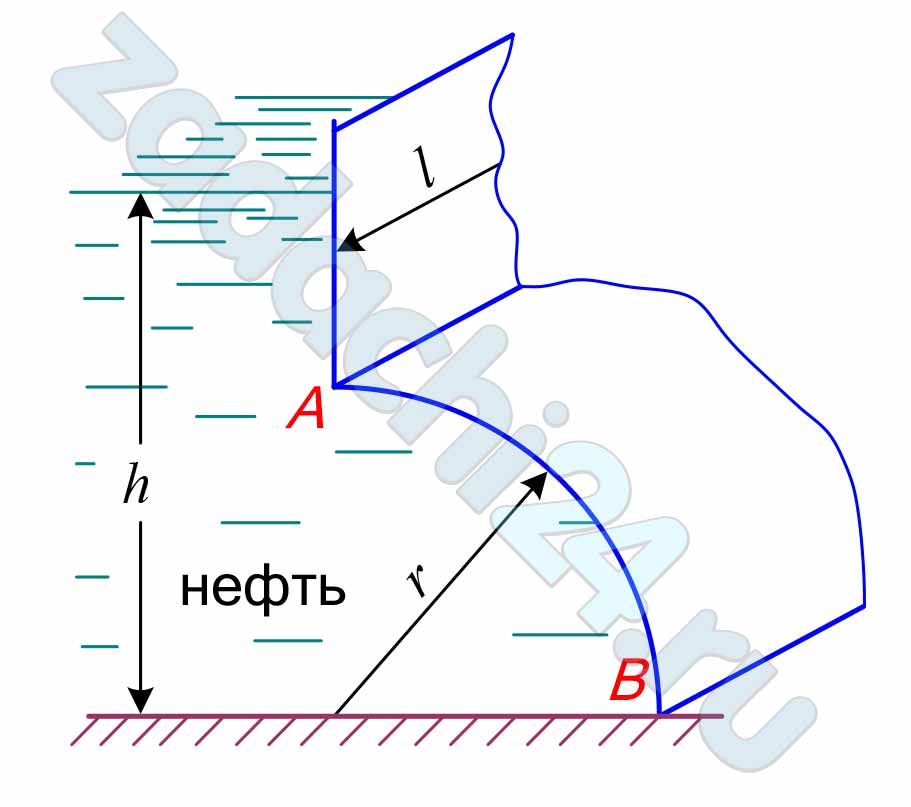
Таблица – Исходные данные
| Вариант | h, м | r, м | l, м |
| 4 | 1,4 | 0,6 | 3,0 |
4.189 Определить силу давления жидкости Р на полусферическую крышку (рис. 4.47) и угол ее наклона к горизонту α при следующих данных: радиус сферы R = 1,6 м, плотность жидкости ρ = 950 кг/м³, избыточное давление в резервуаре р0и = 18 кПа, глубина жидкости Н = 2,5 м.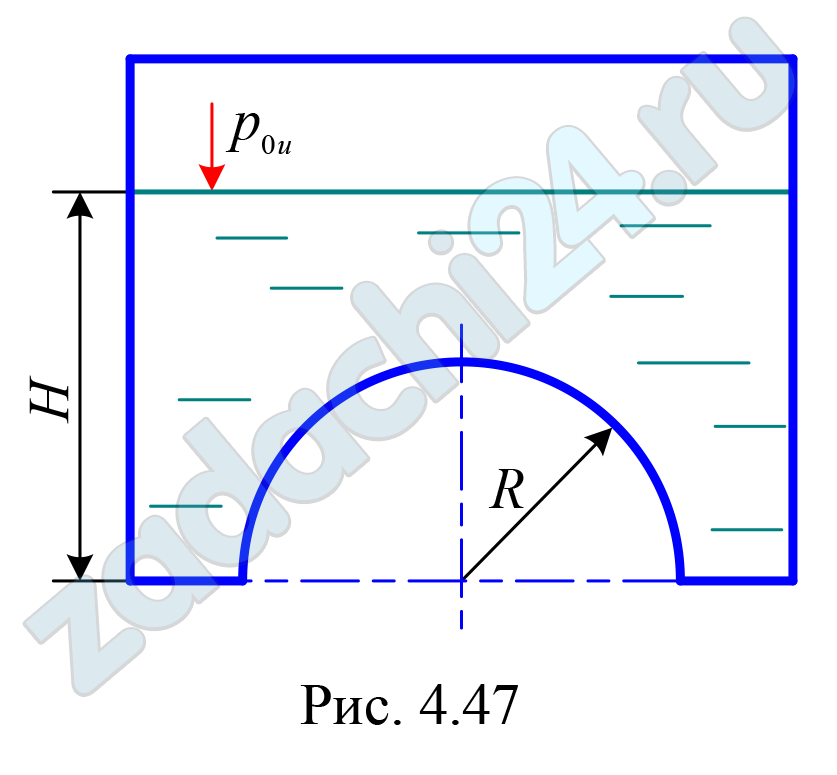
4.190 В боковой плоской стенке закрытого резервуара установлена полусферическая крышка, входящая внутрь резервуара (рис. 3.34).
Определить равнодействующую давления бензина на полусферическую крышку АСВ радиусом r, показать линию действия силы, рассчитать угол наклона силы к горизонту и глубину точки приложения силы к криволинейной поверхности.
На уровне нижней кромки крышки показание манометра равно рман. Принять плотность бензина ρбенз.
Чертеж представить в масштабе.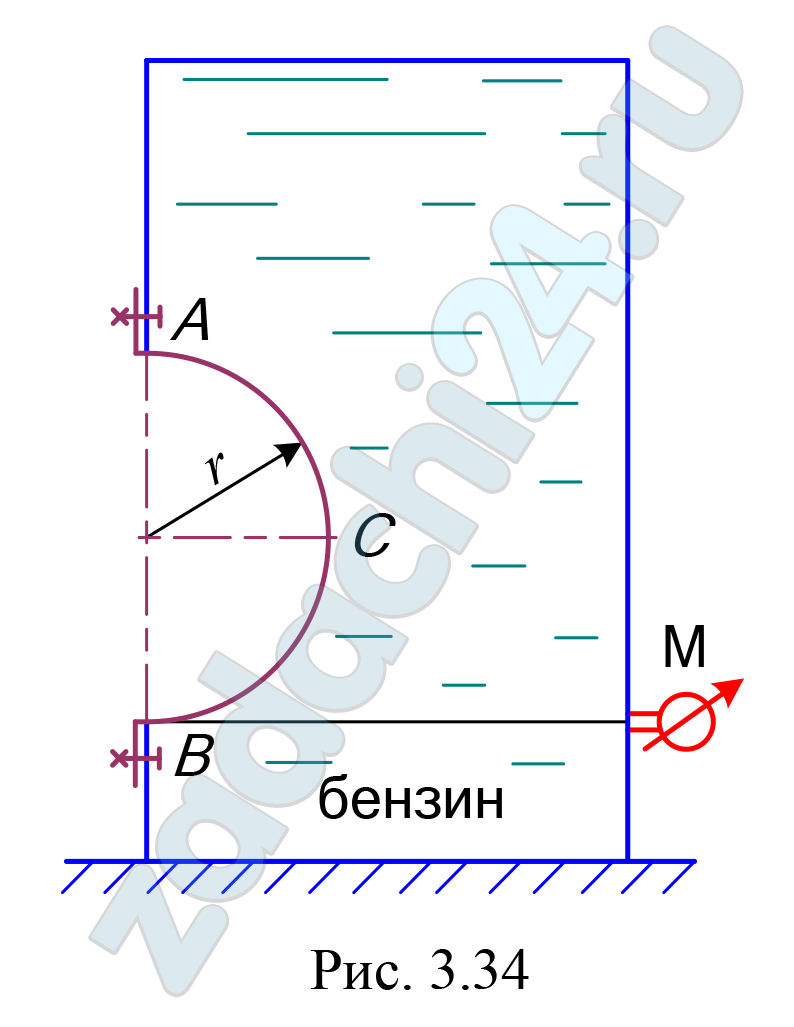
Таблица 1 – Исходные данные
| Вариант | r, мм | рман, ат | ρбенз, кг/м³ |
| а | 300 | 0,09 | 750 |
ВУЗ: УГГУ






