4 Пространственная система сил
4.1 (Вариант 1) Найти реакции опор пространственной конструкции. Схемы конструкций представлены на рис.0-9. Необходимые для расчета данные приведены в таблице С2. В точке А в задаче 3 расположен подпятник, в остальных — шаровой шарнир. В точке В во всех задачах — цилиндрический шарнир (подшипник).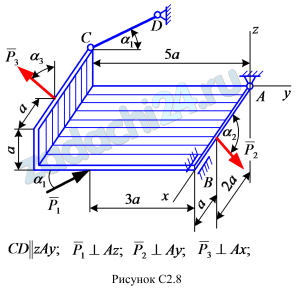
Таблица С2
| Р1, кН | Р2, кН | Р3, кН | α1, град | α2, град | α3, град | а, м |
| 6 | 0 | 4 | 60 | 30 | 45 | 0,5 |
Ответ: ХА=3 кН, RC=3,23 кН, ZB=1,9 кН, ZA=-7,53 кН, YB=-1,11 кН, YA=-2,90 кН.
4.2 Плита, весом Р, нагружена сосредоточенными силами S и Q (положительное направление векторов сил соответствует изображенному на рисунках, а отрицательное направлено противоположно изображенному).
Определить реакции в сферическом и цилиндрических шарнирах, а также реакции в невесомых стержнях.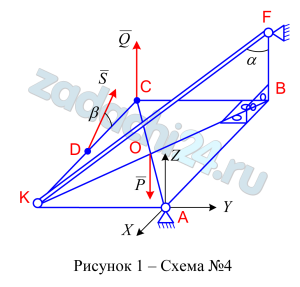
Таблица 1 – Исходные данные
| Вариант 1244 | ||||
| Р, кН | АВ, см | α, град | S, кН | ВС, см |
| 12 | 50 | 15 | -4 | 46 |
Продолжение таблицы 1
| β, град | Q, кН | CD, см | DE, см | № схемы |
| 20 | 7 | 30 | 18 | 4 |
4.3 (Вариант 15) Задача С.7. Определение реакций опор твердого тела
Найти реакции конструкции. Схемы конструкций показаны на рис. 44-46. Необходимые для расчета данные приведены в табл. 14.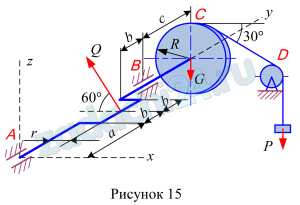
Таблица 14 – Исходные данные
| Силы, кН | Размеры, см | ||||||
| Q | T | G | a | b | c | R | r |
| 3 | - | 2 | 60 | 20 | 40 | 20 | 5 |
Ответ: RA=1,778 кН, RB=1,391 кН, Р=0,650 кН.
4.4 Пространственная сходящаяся система сил
Для заданной пространственной стержневой системы найти усилия в стержнях. Схемы заданий – на рис. 18. Для всех вариантов: Р=2000 Н, АВ=4 м, АС=3 м, AD=6 м.
Примечания: 1. При проецировании сил на оси координат обозначения требуемых углов произвольны.
2. При проецировании силы, идущей вдоль диагонали параллелепипеда, на оси координат рекомендуется использовать правило двойного проецирования.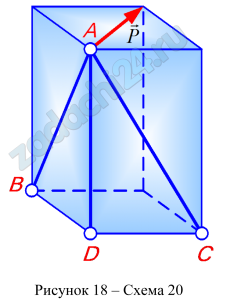
Ответ: SC=2685 H, SB=2883 H, SD=4799 H, стержень AD сжат, а стержни AB и AC растянуты.
4.5 Пространственная произвольная система сил
Вал редуктора установлен на двух подшипниках – радиальном и радиально – упорном. Определить реакции в подшипниках и величину силы F1 (для вариантов 1-12) или силы T (для вариантов 13-24). Схемы заданий приведены на рис. 21. Принять F=4 кН, d=100 мм, d1=250 мм (для вариантов 1-12), (для вариантов 13-24) а=100 мм, α=30º. Принять Fr=0,372F; Fa=0,2126F.
Ответ: ХА=1,801 кН, ZA=1,350 кН, ХВ=4,797 кН, YB=0,850 кН, ZB=1,362 кН, RA=2,251 кН, RB=4,987 кН, Т=1 кН.
4.6 (Вариант 2) Задача С.2. Равновесие вала
К валу со шкивами радиусов R, r, установленному в радиально – упорном и радиальном подшипниках A и B приложены силы P, Q, G. Сила Q расположена в плоскости шкива радиуса R и направлена по касательной к его окружности. Размеры, углы и величины сил Q, G приведены в табл. 1.2.
Определить величину силы P при равновесии вала, а также реакции подшипников A и D.
Указания
При вычислении момента силы Q относительно координатных осей, перпендикулярных оси вала, удобно разложить ее на две составляющие, расположенные в плоскости диска и параллельные этим осям. Необходимо помнить, что момент силы относительно оси равен нулю, если линия действия силы параллельна или пересекает ее.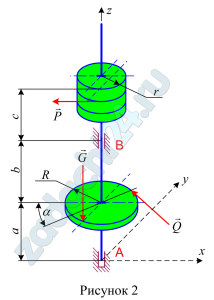
Таблица 1.2 – Исходные данные
| а, м | b, м | c, м | r, м | R, м | α, град | Q, H | G, H |
| 0,4 | 0,4 | 0,2 | 0,1 | 0,4 | 30 | 100 | 200 |
Ответ: P=400 H, RA=258 H, RB=528 H.
4.7.0 (Вариант 11) РАСЧЕТНАЯ РАБОТА №4
Равновесие пространственной системы сил
Однородная прямоугольная плита ABCD веса G закреплена в точке A и B цилиндрическим шарниром и поддерживается в горизонтальном положении тросом KC (вар. 12) и KD (вар. 13) или невесомым стержнем KD (вар. 9-11, 17), расположенным в вертикальной плоскости и образующим с горизонтальной плоскостью плиты угол β. В вар. 14 плита опирается на острие в точке E. На плиту действует сосредоточенная нагрузка F, образующая угол α с плоскостью плиты. Определить реакции шарниров A и B и натяжение троса T или усилие в невесомом стержне S. Необходимые линейные размеры, углы, величины сил приведены в табл. 4.1.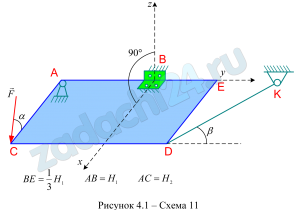
Таблица 4.1- Исходные данные к расчетной работе №4
| Номер схемы | Линейные размеры, м | Силы, Н | Плоскость, в которой лежит сила F | Углы, º | ||||
| H1 | H2 | KD | F | G | ||||
11 | 2,0 4,0 3,0 | 2,0 3,5 2,0 | 10 15 30 | 30 35 40 | Параллельна плоскости Bxz | 30 30 30 | 60 60 60 |
|
4.8 (Вариант 531) Тема «Пространственная система сил»
На горизонтальный вал насажены колесо 1 радиусом r1=20 см, колесо 2 радиусом r2=30 см и прикреплен перпендикулярно оси вала (параллельно оси х) рычаг СD длиной l=20 см. К одному колесу приложена сила F, образующая с горизонталью угол α1, а к другому – сила Т2, образующая с вертикалью угол α2; к рычагу приложена вертикальная сила Р (рис. 4, схемы 4 – 7). Пренебрегая весом вала, колес и рычага, определить силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В.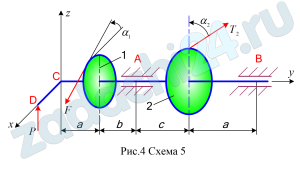
Таблица 3
| Номер условия | Номер схемы (рис. 4) | Расстояния, м | Силы, Н | Углы, град | ||||
| a | b | c | F | T2 | α1 | α2 | ||
| 2 | 5 | 1,4 | 1,5 | 1,4 | 1000 | 300 | 0 | 60 |
Ответ: Р=610,30 Н, RАХ=-1405,81 Н, RAZ=-1317,40 Н, RА=1926,62 Н, RВХ=665,61 Н, RВZ=557,10 Н, RВ=867,98 Н.
4.9.0 Равновесие пространственной произвольной системы сил
Однородная прямоугольная плита АВСD весом 200 Н закреплена, как показано на рисунке. Определить реакции связей, если АВ=DC=a, AD=BC=b (рисунок 1).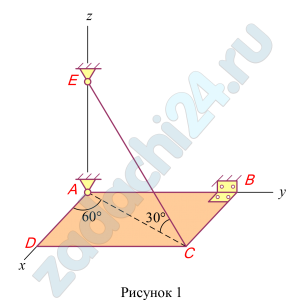
Исходные данные: G=200 Н, а=2 м, b=2 м, СЕ=2/3а м.
Ответ: RA=318,85 Н, RB=175,20 Н, RC=200 Н.
4.10 Задача С2.00 Определение реакций опор твёрдого тела
(пространственная система сил)
Определить значение силы Р и реакции опор твёрдого тела, изображённого на рис. С2.0 – С2.9. Исходные данные для расчёта представлены в таблице С2.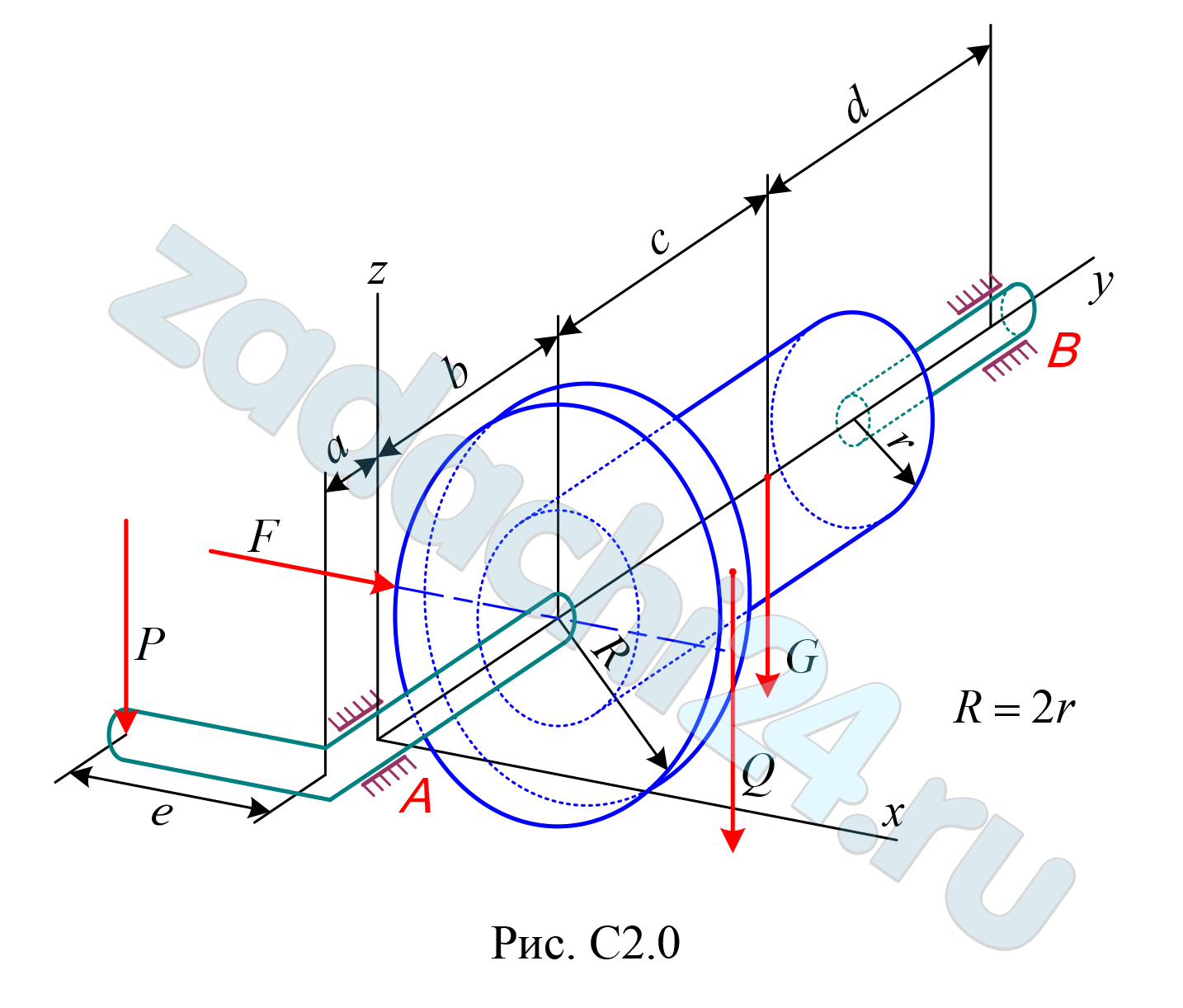
Таблица С2
| Номер условия | Q, кН | F, кН | G, кН | а, м | b, м | с, м | d, м | е, м | r, м | α, град |
| 0 | 8 | 4 | 10 | 1 | 2 | 2 | 2 | 1 | 1 | 30 |
