2 Произвольная плоская система сил
2.1 Задача С1 Равновесие произвольной плоской системы сил
(Определение реакций опор твёрдого тела)
Найти реакции опор конструкции, схема которой изображена на рис. С1.0–С1.9. Необходимые исходные данные представлены в таблице С1.
Таблица С1
| Номер условия | Р, кН | F, кН | М, кН·м | q, кН/м | α, град | β, град |
| 0 | 10 | 30 | 5 | 20 | 30 | 60 |
Номер условия: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
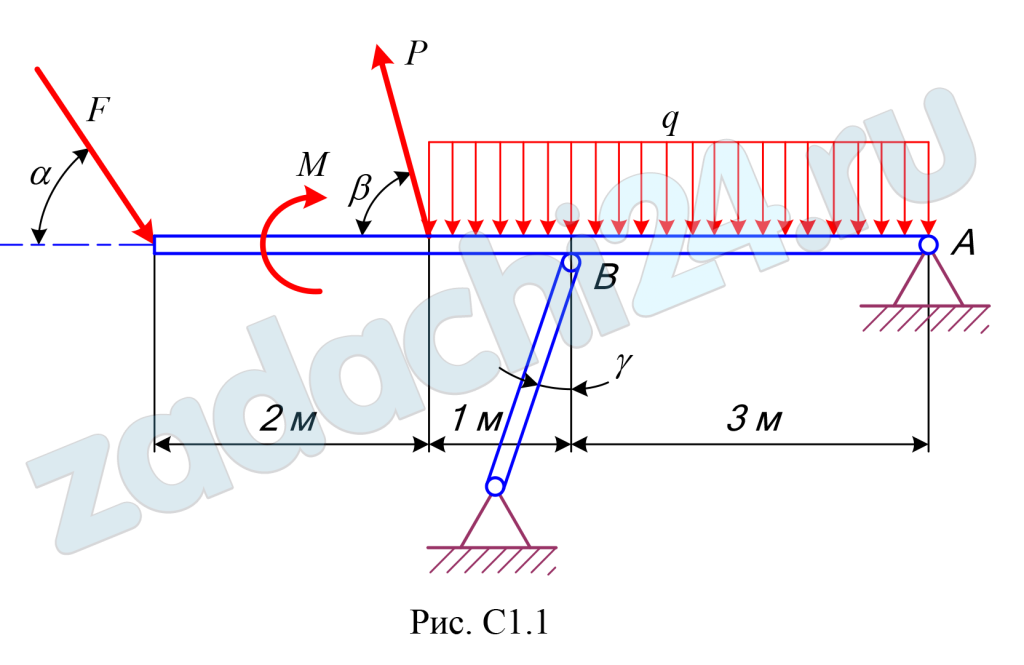
2.2 Задача С1.01 Равновесие произвольной плоской системы сил
(Определение реакций опор твёрдого тела)
Найти реакции опор конструкции, схема которой изображена на рис. С1.0–С1.9. Необходимые исходные данные представлены в таблице С1.
Таблица С1
| Номер условия | Р, кН | F, кН | М, кН·м | q, кН/м | α, град | β, град | γ, град |
| 0 | 10 | 30 | 5 | 20 | 30 | 60 | 45 |
Варианты задачи: 1, 2, 3, 4, 5, 6, 7, 8, 9.
ВУЗ: СамГУПС
2.3 Определить реакции в опорах А и В балки (рис. 2.1). Опора шарнирно — неподвижная. Исходные данные приведены в табл. 2.1.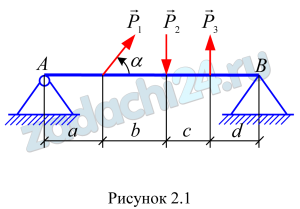
Таблица 2.1
| Вариант 7 | |||||||
| а, м | b, м | с, м | d, м | α, град | Р1, Н | Р2, Н | Р3, Н |
| 1 | 3 | 2 | 4 | 210 | 9 | 14 | 18 |
2.4 Определить реакции в опорах А и В балки (рис.3.1). Опора шарнирно-неподвижная. Исходные данные приведены в табл. 3.1.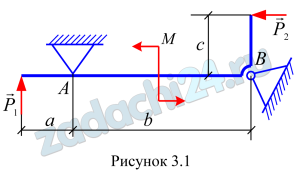
Таблица 3.1
| Вариант 7 | |||||
| а, м | b, м | с, м | Р1, Н | Р2, Н | М, Н·м |
| 1 | 3 | 2 | 9 | 14 | 2 |
2.5 Определить реакции и момент заделки в точке А консольной балки (рис.4.1). Исходные данные приведены в табл.4.1.
Таблица 4.1 — Исходные данные
| Вариант 7 | |||||||
| а, м | b, м | l, м | Р1, Н | Р2, Н | М, Н·м | q, Н/м | α, град |
| 1 | 3 | 2 | 9 | 14 | 2 | 14 | 210 |
2.6 Определить реакции опор двухопорной балки (рис.6.1). Исходные данные — в табл.6.1.
Таблица 6.1 — Исходные данные
| Номер схемы | Вариант | М, Н·м | F, H | q, Н/м |
| 7 | 17 | 4 | 10 | 5 |
2.7 Невесомая балка АВС закреплена с помощью неподвижного шарнира в точке А, и невесомого стержня в точке В. В точке С балки прикреплена нить, которая перекинута через блок, к свободному концу которой подвешен груз весом Р.
Определить по теореме о трех силах величину реакции в неподвижном шарнире, а также усилие в невесомом стержне BD.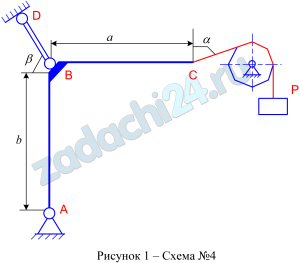
Таблица 1 – Исходные данные
| Вариант 1244 | |||||
| а, см | β, град | b, см | α, град | Р, Н | № схемы |
| 17 | 60 | 12 | 120 | 70 | 4 |
ВУЗ: ЮУрГУ
2.8 Две невесомые балки соединены между собой промежуточным шарниром и нагружены сосредоточенными силами F и P, сосредоточенной парой сил с моментом M и распределенными нагрузками интенсивности q1 и q2 (положительное направление векторов сил и пары сил соответствует изображенному на рисунках, а отрицательное направлено противоположно изображенному).
Определить реакции невесомых балок и давление в промежуточном шарнире.
Таблица 1 – Исходные данные
| Вариант 1244 | ||||
| а, см | q2, Н/м | М, Н·м | β, град | b, см |
| 10 | -80 | 5 | 60 | 25 |
Продолжение таблицы 1
| F, H | α, град | q1, Н/м | с, см | Р, Н | № схемы |
| -4 | 45 | -50 | 18 | 14 | 4 |
ВУЗ: ЮУрГУ
2.9 Определить реакции связей балки АВ (рисунок 1).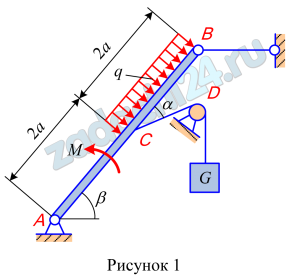
Таблица 1 – Исходные данные
| G, кН | М, кН·м | q, кН/м | а, м | α, град | β, град |
| 6 | 6 | 2 | 1,5 | 30 | 60 |
Ответ: RA=4,6 кН, RB=-5,77 кН.
Скачать файл (банки РФ) 200 RUB2.10 Определить реакции связей ломанного стержня АСВ, изображенного на рисунке 1. В точке D закреплен канат, переброшенный через блок K и несущий на конце тело G.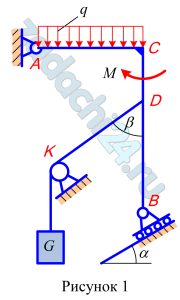
Таблица 1 – Исходные данные
| G, кН | М, кН·м | q, кН/м | AC=BD, м | CD, м | α, град | β, град |
| 4 | 6 | 3 | 2 | 1 | 30 | 60 |
Ответ: RB=88,36 кН, RA=83 кН.
Скачать файл (банки РФ) 200 RUB