Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике
15.3 Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
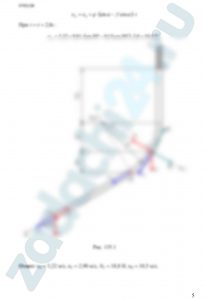
Вариант 6 (рис. 117, схема 2). Лыжник подходит к точке А участка трамплина АВ, наклоненного под углом α к горизонту и имеющего длину l, со скоростью υА. Коэффициент трения скольжения лыж на участке АВ равен f. Лыжник от А до В движется τ с; в точке В со скоростью υВ он покидает трамплин. Через Т с лыжник приземляется со скоростью υС в точке С горы, составляющей угол β с горизонтом.
При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха.
Дано: α = 20º; f = 0,1; τ = 0,2 с; h = 40 м; β = 30º. Определить l и υС.
15.4 Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
Вариант 8 (рис. 117, схема 2). Лыжник подходит к точке А участка трамплина АВ, наклоненного под углом α к горизонту и имеющего длину l, со скоростью υА. Коэффициент трения скольжения лыж на участке АВ равен f. Лыжник от А до В движется τ с; в точке В со скоростью υВ он покидает трамплин. Через Т с лыжник приземляется со скоростью υС в точке С горы, составляющей угол β с горизонтом.
При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха.
Дано: υА = 21 м/с; f = 0; τ = 0,3 с; υВ = 20 м/с; β = 60º. Определить α и d.
Скачать файл (банки РФ) 250 RUB15.6 Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
Найти уравнения движения тела М массой m (рис. 119-121), принимаемого за материальную точку и находящегося под действием переменной силы Р = Xi + Yj + Zk, при заданных начальных условиях. Во всех вариантах ось z (где показана) вертикальная, за исключением вариантов 8 и 30.
Необходимые для решения данные приведены в табл. 39, в которой приняты следующие обозначения: i, j, k, — орты координатных осей (соответственно х, у, z); g – ускорение свободного падения (9,81 м/с²); f – коэффициент трения скольжения; t – время, с; х, у, z, х′, у′, z′ — координаты точки и проекции ее скорости на оси координат соответственно, м и м/с.
Во всех случаях, где сила зависит от х, х′, у′, z′, рассмотреть движение точки, при котором эти величины только положительны.
Таблица 39
| Номер варианта (рис. 119-121) | m, кг | , Н | Начальные условия | ||||||
| f | х0 | у0 | z0 | х′0 | у′0 | z′0 | |||
| м | м/c | ||||||||
| 8 | 150 | 0 | 0 | 0 | 0 | 0,5 | 2 | 0 | |
15.7 Применение основных теорем динамики к исследованию движения материальной точки
Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости (рис. 135-137). Найти скорость шарика в положениях В и С и давление шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь h0, отделяется от пружины.
Необходимые для решения данные приведены в табл. 42.
Таблица 42
| Номер варианта (рис. 135-137) | m, кг | υА, м/с | τ, с | R, м | f |
| 3 | 0,4 | 0 | 2,0 | 0,2 | 0,15 |
Конец таблицы 42
| α, град | β, град | h0, см | с, Н/см | Величины, которые требуется
определить дополнительно |
| 30 | — | 10 | 1 | υD |
В задании приняты следующие обозначения: m – масса шарика; υА – начальная скорость шарика; τ – время движения шарика на участке АВ (в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке BD (в вариантах 3, 4, 6, 7, 9 – 13, 15 – 17, 19, 22, 25, 26, 28, 29); f – коэффициент трения скольжения шарика по стенке трубки; h0 – начальная деформация пружины; h – наибольшее сжатие пружины; с – коэффициент жесткости пружины; Н – наибольшая высота подъема шарика; s – путь, пройденный шариком до остановки.
Скачать файл (банки РФ) 250 RUB15.5 Применение основных теорем динамики к исследованию движения материальной точки
Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости (рис. 135-137). Найти скорость шарика в положениях В и С и давление шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь h0, отделяется от пружины.
Необходимые для решения данные приведены в табл. 42.
Таблица 42
| Номер варианта (рис. 135-137) | m, кг | υА, м/с | τ, с | R, м | f |
| 8 | 0,2 | 1 | 0,5 | 1,5 | 0,15 |
Конец таблицы 42
| α, град | β, град | h0, см | с, Н/см | Величины,
которые требуется определить дополнительно |
| 30 | 60 | 0 | 4 | h |
В задании приняты следующие обозначения: m – масса шарика; υА – начальная скорость шарика; τ – время движения шарика на участке АВ (в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке BD (в вариантах 3, 4, 6, 7, 9 – 13, 15 – 17, 19, 22, 25, 26, 28, 29); f – коэффициент трения скольжения шарика по стенке трубки; h0 – начальная деформация пружины; h – наибольшее сжатие пружины; с – коэффициент жесткости пружины; Н – наибольшая высота подъема шарика; s – путь, пройденный шариком до остановки.
Скачать файл (банки РФ) 250 RUB