Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике
2.12 Задание С.1. Определение реакций опор твердого тела
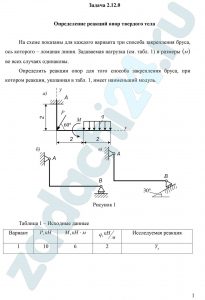
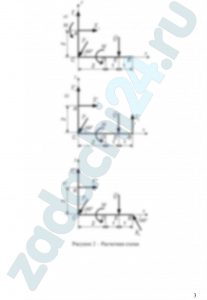
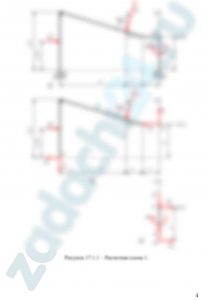
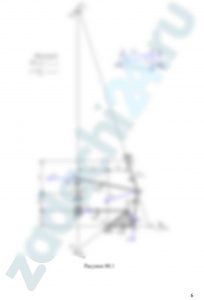
На схеме показаны для каждого варианта три способа закрепления бруса, ось которого – ломаная линия. Задаваемая нагрузка (см. табл. 1) и размеры (м) во всех случаях одинаковы.
Определить реакции опор для того способа закрепления бруса, при котором реакции, указанная в табл. 1, имеет наименьший модуль.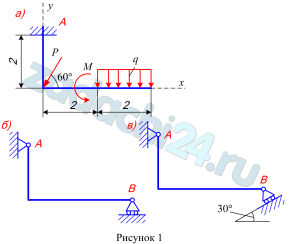
Таблица 1
| Вариант | Р, кН | М, кН·м | q, кН/м | Исследуемая реакция |
| 1 | 10 | 6 | 2 | YA |
2.13 Задание С.3. Определение реакций опор составной конструкции (система двух тел)
Определить реакции опор, а также соединения С для того способа сочленения (шарнир или скользящая заделка), при котором модуль реакции опоры А наименьший.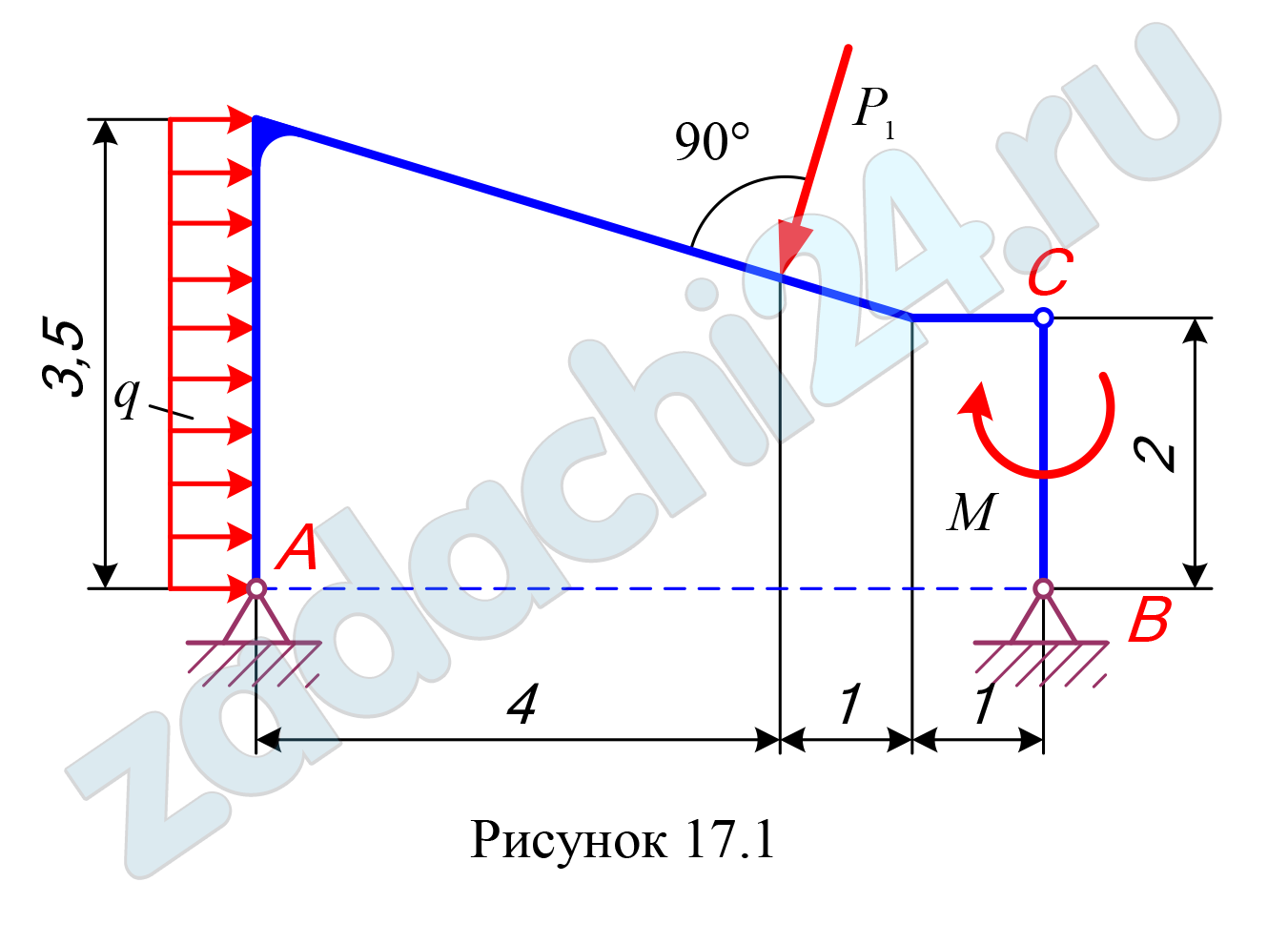
Таблица 5
| Вариант | Р1 | Р2 | М, кН·м | q, кН/м | Исследуемая реакция |
| кН | |||||
| 1 | 5,0 | — | 24,0 | 0,8 | ХА |
Варианты задачи: 10.
3.2 (Вариант 2) Задание С.5. Определение реакций опор твердого тела
Определить минимальное (в вариантах 1-20, 25, 26, 29, 30) или максимальное (в вариантах 21-24, 27, 28) значение силы Р и реакции опор системы, находящейся в покое. Схемы вариантов представлены на рис. 32-34. а необходимые для расчета данные – в табл. 10.
В вариантах 1-20 сцепление (трение покоя) учесть только между колодкой и барабаном. В вариантах 21-30 учесть сцепление в двух опорных точках тела весом G.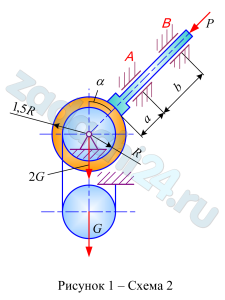
Таблица 10
| G | Q | a | b | c | α, град | Коэффициент сцепления (коэффициент трения покоя) |
Точки, в которых определяются реакции |
| кН | м | ||||||
| 1,1 | — | 0,10 | 0,15 | — | 30 | 0,15 | О, А, В |
2.60 Определение реакций опор составной конструкции (система двух тел)
Найти реакции опор и давление в промежуточном шарнире составной конструкции. Схемы конструкций представлены на рис. 27-29. (размеры – в мм), нагрузка указана в табл. 6.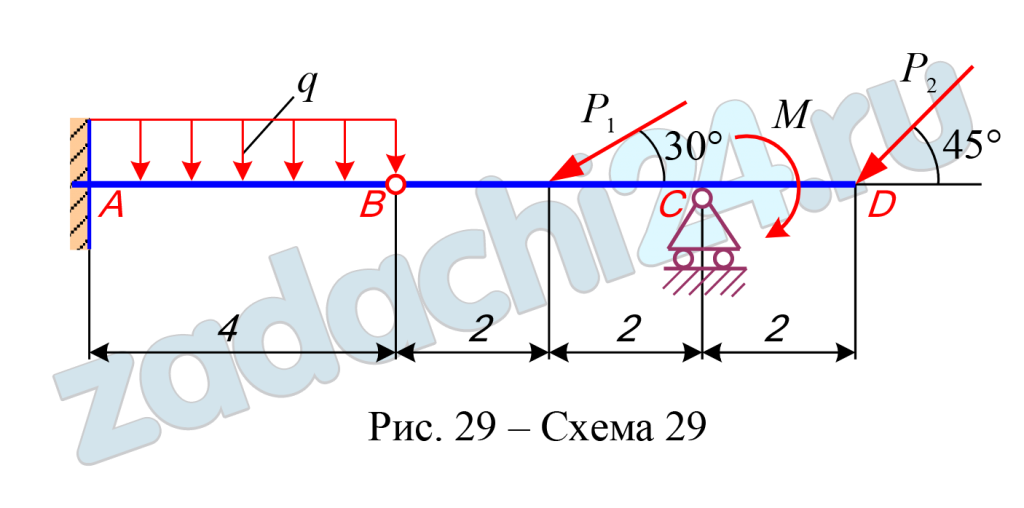
Таблица 6
| Номер варианта | Р1 | Р2 | М, кН⸱м | q, кН/м |
| кН | ||||
| 29 | 10,0 | 9,0 | 35,0 | 1,3 |
4.3 (Вариант 15) Задача С.7. Определение реакций опор твердого тела
Найти реакции конструкции. Схемы конструкций показаны на рис. 44-46. Необходимые для расчета данные приведены в табл. 14.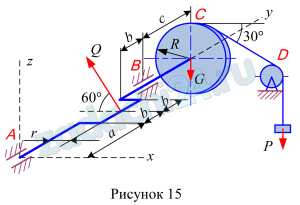
Таблица 14 – Исходные данные
| Силы, кН | Размеры, см | ||||||
| Q | T | G | a | b | c | R | r |
| 3 | — | 2 | 60 | 20 | 40 | 20 | 5 |
5.2 (Вариант 1) Задание С.8. Определение положения центра тяжести тела
Найти координаты центра тяжести плоской фермы, составленной из тонких однородных стержней одинакового погонного веса (варианты 1-6), плоской фигуры (варианты 7-18 и 24-30) или объема (варианты 19-23), показанных на рис. 49-51. В вариантах 1-6 размеры указаны в метрах, а в вариантах 7-30 – в сантиметрах.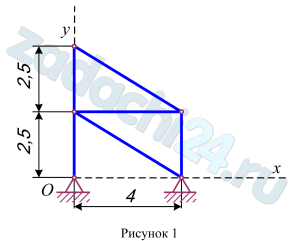
6.7 Задание К.1. Определение скорости и ускорения точки по заданным уравнениями ее движения
По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t=t1(c) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории.
Необходимы для решения данные приведены в табл. 20.
Таблица 20
| Номер варианта | Уравнения движения | t=t1c | |
| x=x(t), см | у=у(t), см | ||
| 1 | -2t² + 3 | -5t | 1/2 |
9.1 (Вариант 2) Задание К.2. Определение скоростей и ускорений точек твердого тела при поступательном и вращательном движениях
Движение груза 1 должно описываться уравнением
x=c2t2+c1t+c0, (1)
где t — время, c; c, c0-2 — некоторые постоянные.
В начальный момент времени (t=0) координата груза должна быть x0, а его скорость — υ0.
Кроме того, необходимо, чтобы координата груза в момент времени t=t2 была равна x2.
Определить коэффициенты c0, c1 и c2, при которых осуществляется требуемое движение груза 1. Определить также в момент времени t=t1 скорость и ускорение груза и точки M одного из колес механизма.
Схемы механизмов показаны на рис. 68 – 70, а необходимые данные приведены в табл. 23.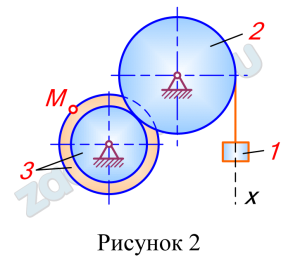
Таблица 23
| Радиусы, см | Координаты и скорости груза 1 |
Расчетные моменты времени, с |
||||||
| R2 | r2 | R3 | r3 | х0, см | υ0, см/c | х2, см | t2 | t1 |
| 80 | — | 60 | 45 | 5 | 10 | 41 | 2 | 1 |
9.2 (Вариант 2) Задание К.3. Кинематический анализ плоского механизма
Найти для заданного положения механизма скорости и ускорения точек В и С, а также угловую скорость и угловое ускорение звена, которому эти точки принадлежат. Схемы механизмов помещены на рис. 73 – 75, а необходимые для расчета данные приведены в табл. 25.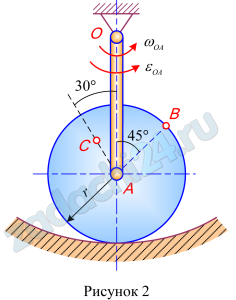
Таблица 25
| Размеры, см | ωОА, рад/c | ω1, рад/c | εОА, радc2 | υА, см/c | аА, см/c2 | |||
| OA | r | AB | AC | |||||
| 30 | 15 | — | 8 | 3 | — | 2 | — | — |
Примечание. ωОА и εОА — угловая скорость и угловое ускорение кривошипа ОА при заданном положении механизма; ω1 — угловая скорость колеса I (постоянная); и υА — аА скорость и ускорение точки А. Качение колес происходит без скольжения.
Скачать файл (банки РФ) 350 RUB7.2 Кинематический анализ многозвенного механизма
Кривошип О1А вращается с постоянной угловой скоростью ωО1А = 2 рад/с. Определить для заданного положения механизма:
1) скорости точек А, В, С, … механизма и угловые скорости всех его звеньев с помощью плана скоростей;
2) скорости этих же точек механизма и угловые скорости звеньев с помощью мгновенных центров скоростей;
3) ускорения точек А и В и угловое ускорение звена АВ;
4) положение мгновенного центра ускорений звена АВ;
5) ускорение точки М, делящей звено АВ пополам.
Схемы механизмов показаны на рис. 80-83, а необходимые для расчета данные приведены в табл. 27.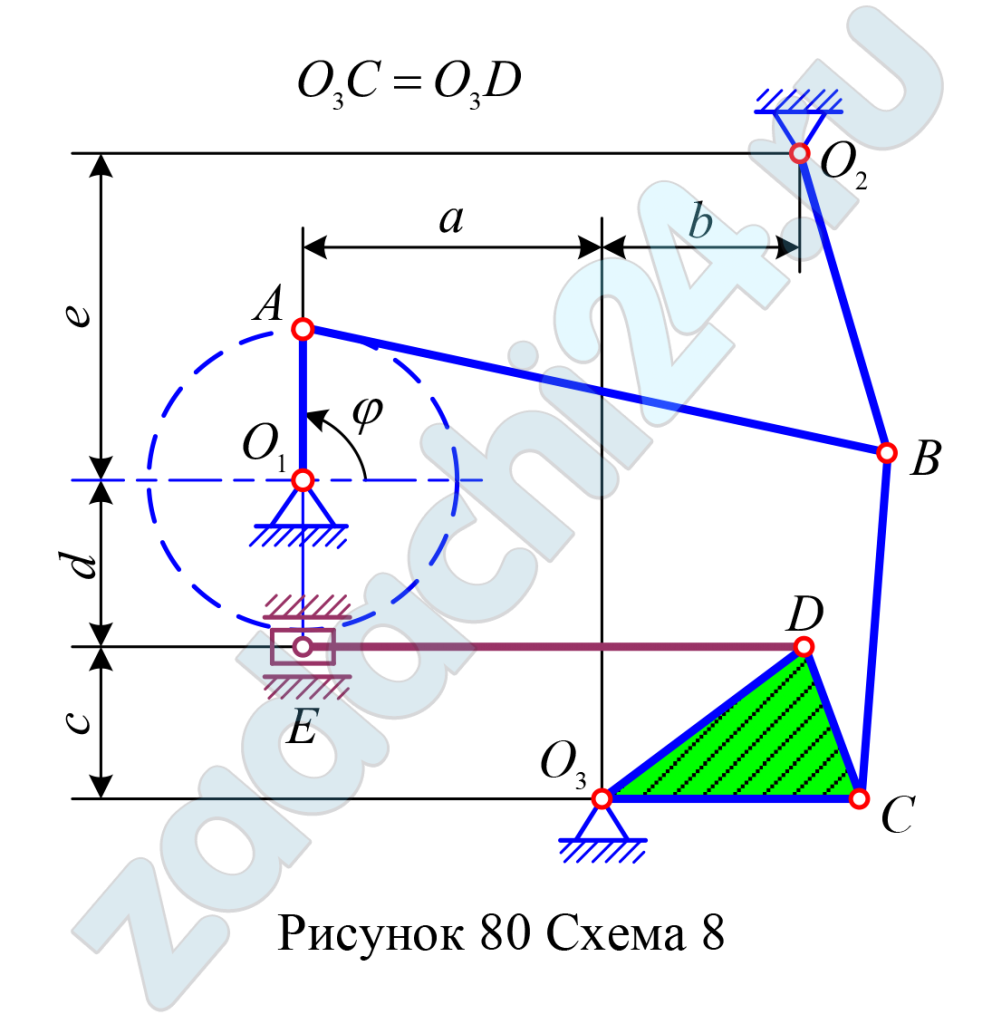
Таблица 27
| Номер варианта (рис. 80-83) | φ, град | Расстояния, см | ||||
| a | b | c | d | e | ||
| 8 | 90 | 27 | 18 | 14 | 15 | 30 |
Конец таблицы 72
| Длина звеньев, см | ||||||
| О1А | О2В | O3D | АВ | ВС | CD | DE |
| 14 | 29 | 23 | 55 | 32 | 15 | 45 |