Теоретическая механика Московский Политех
7.20 РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА К-3
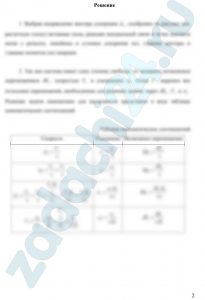
В планетарном механизме (рис.3.1-3.6) шестерня I радиуса R1 неподвижна, а кривошип OA, вращаясь вокруг неподвижной оси, проходящей через точку O перпендикулярно плоскости рисунка, приводит в движение свободно насаженную на его конец A шестерню II радиуса R2 . Для указанного на рисунке положения механизма найти скорости и ускорения точек A и B, если для соответствующего момента времени известны абсолютные величины угловой скорости и углового ускорения кривошипа (ωOA, εOA). На рисунках условно показаны направления угловой скорости и углового ускорения дуговыми стрелками вокруг оси вращения. При этом направление угловой скорости соответствует направлению вращательного движения кривошипа. Угловое ускорение направлено в сторону угловой скорости при ускоренном вращении и в противоположную — при замедленном. Необходимые данные приведены в таблице 3.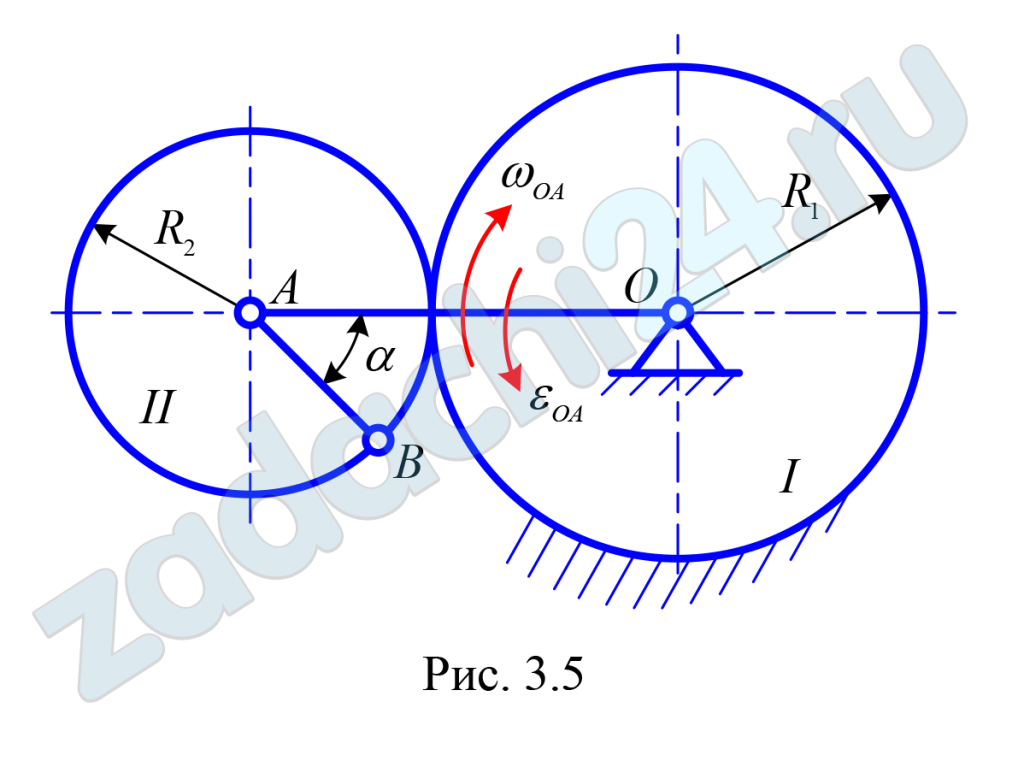
Таблица 3
| № варианта | № рисунка | ωOA, (с-1) | εOA, (с-2) | R1, (м) | R2, (м) | α, (град) |
| 11 | 3.5 | 2 | 4 | 0,7 | 0,2 | 90 |
ВУЗ: Московский Политех
15.8 ЗАДАНИЕ Д-1 Интегрирование дифференциальных уравнений движения материальной точки
Материальная точка M массой m, получив в точке А начальную скорость V0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости. Участки трубы или оба наклонные, или один горизонтальный, а другой наклонный. Угол наклона трубы α = 30º.
На участке АВ на материальную точку действует сила тяжести Р, постоянная сила (ее направление указано на рисунках) и сила сопротивления среды R, зависящая от скорости V груза (направлена сила против движения). Трением груза о трубу на участке АВ пренебрегаем.
В точке В материальная точка, не изменяя величины своей скорости, переходит на участок ВС трубы, где на нее действует сила тяжести P, сила трения (коэффициент трения груза о трубу f = 0,2) и переменная сила F, проекция которой FX на ось x приведена в таблице Д-1.
Известно расстояние AB = l или время t1 движения от точки А до точки В. Требуется найти закон движения материальной точки на участке BС: x = f (t).
Таблица Д-1
| № варианта 6 | ||||||||
| Рис. | m, кг | V0, м/c | Q, Н | R, Н | μ | l, м | t1, с | FX, Н |
| 6 | 1,2 | 22 | 2 | μV² | 0,8 | 0,5 | — | 6t |
ВУЗ: Московский Политех
17.1 ЗАДАНИЕ Д-2 Свободные колебания материальной точки.
Система пружин (рис. 2.1) с жесткостями С1 и С2 в начальный момент недеформирована. Тело весом P совершает колебания, упав с высоты h из состояния покоя или после сообщения ему начальной скорости V0 вниз или вверх. Найти закон колебаний x(t) тела, частоту колебаний k, период Т и амплитуду А этих колебаний. Необходимые данные взять из таблицы Д-2. Условия задачи таковы, что пластины, соединяющие пружины, во время колебаний остаются параллельными своим первоначальным положениям. Пластины и пружины невесомы. Положительное направление оси x вниз. Считать g = 10 м/с². Наклонные плоскости гладкие.
Указание. В заданиях с рисунками 1, 4, 7 определить предварительно V0 , учитывая параметр h.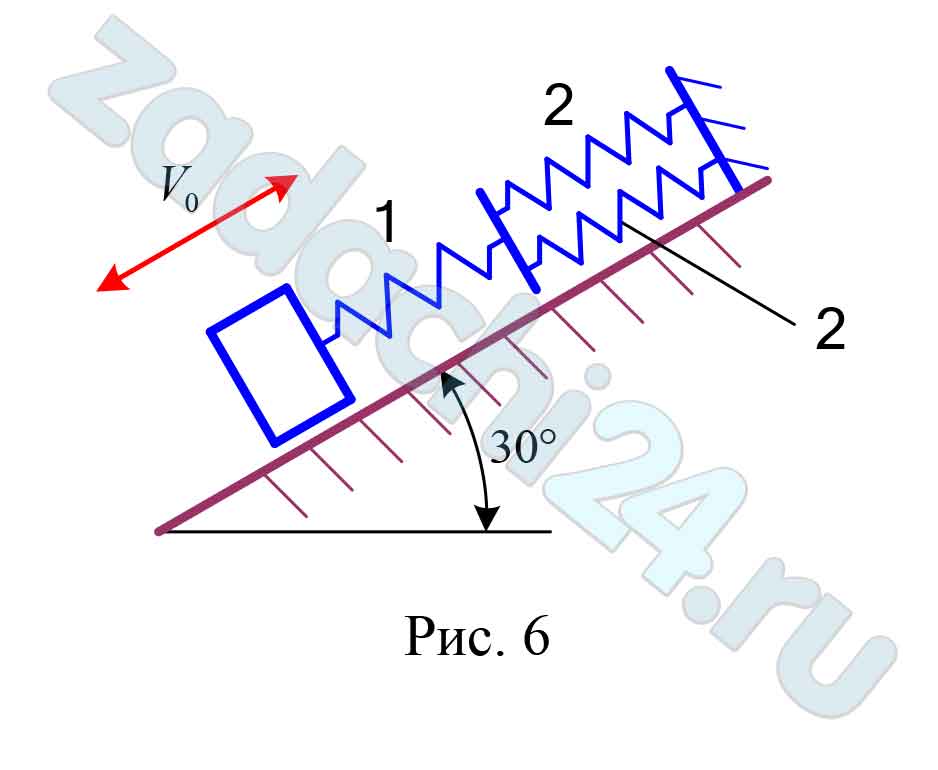
Таблица Д-2
| № варианта | № рисунка | С1, Н/см | С2, Н/см | Р, Н | h, см | V0, см/с |
| 6 | 6 | 150 | 100 | 45 | — | 40, вниз |
ВУЗ: Московский Политех
11.15 ЗАДАНИЕ Д-3
На звено 1 механизма, угловая скорость которого равна ω10, с некоторого момента времени (t = 0) начинает действовать пара сил с моментом M (движущий момент) или движущая сила Р.
Массы звеньев 1 и 2 механизма равны соответственно m1 и m2, а масса поднимаемого груза 3 — m3. Момент сил сопротивления вращению ведомого звена 2 равен МC. Радиусы больших и малых окружностей звеньев 1 и 2: R1, r1, R2, r2 .
Схемы механизмов показаны на рис. 3.1-3.3, а необходимые для решения данные приведены в табл. 3.1.
Найти уравнение вращательного движения звена механизма, указанного в последней графе табл. 3.1. Определить также натяжение нитей в заданный момент времени, а в вариантах, где имеется соприкасание звеньев 1 и 2, найти окружное усилие в точке их касания. Звенья 1 и 2, для которых радиусы инерции ρ1 и ρ2 в табл. 3.1 не заданы, считать сплошными однородными дисками.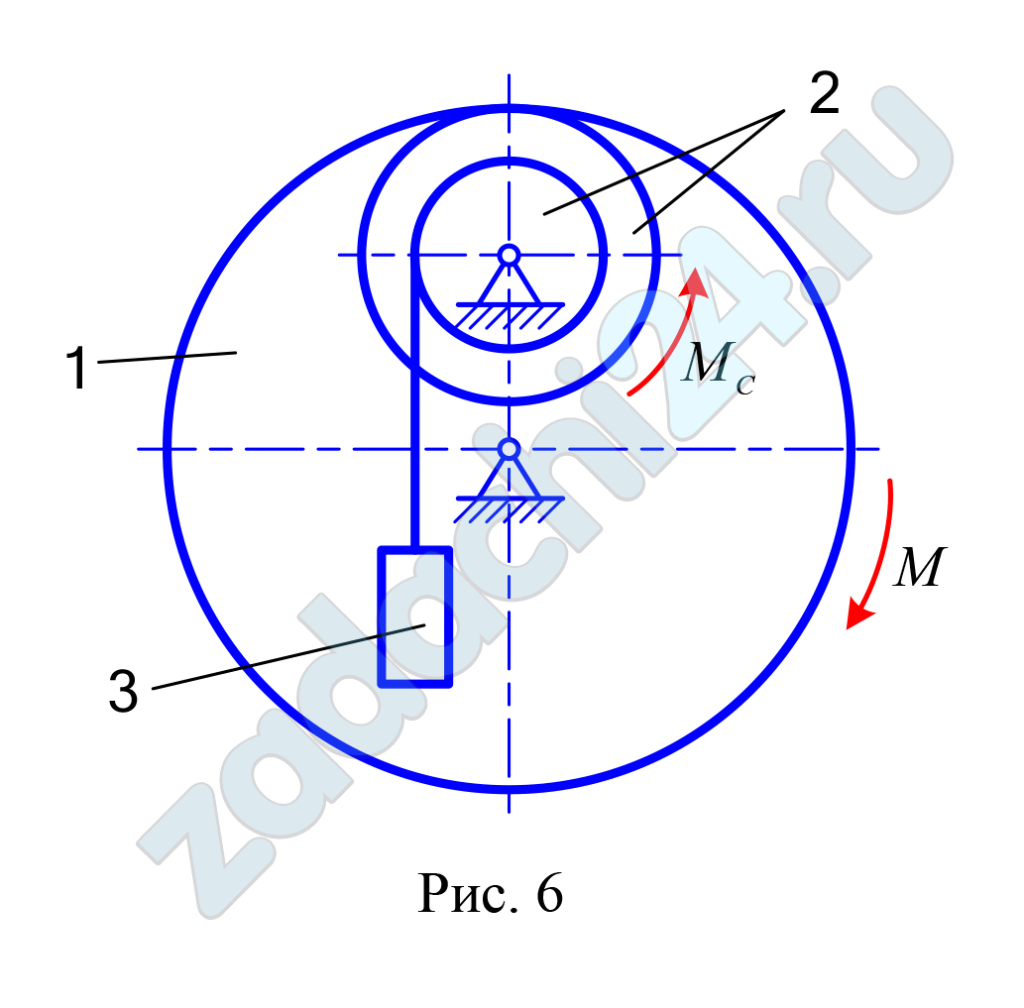
Таблица Д-3
| № варианта | m1, кг | m2, кг | m3, кг | R1, см | R2, см | r2, см |
| 6 | 400 | 250 | 600 | 70 | 30 | 20 |
Продолжение таблицы Д-3
| ρ1, см | ρ2, см | М, Н·м | МС, Н·м | ω10, с-1 | t, с | Найти |
| 70 | 20√2 | 4800+10е2t | 800 | 3 | 4 | φ1 |
ВУЗ: Московский Политех
15.9 ЗАДАНИЕ Д-4
Плоскопараллельное движение твердого тела
Барабан радиуса R весом P имеет проточку (как у катушки) радиуса r = 0,5R (рис.4.1, табл. Д-4). К концам намотанных на барабан нитей приложены постоянные силы и , направления которых определяются углом β. Кроме сил на барабане действует пара с моментом M. При движении, начинающимся из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс барабана, т.е. xC = f(t) , и наименьшее значение коэффициента трения fmin о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.
Таблица Д-4
| № варианта | № рисунка | α,º | β,º | F1 | F2 | М |
| 6 | 6 | 0 | 60 | 0,3Р | 0,1Р | 0 |
ВУЗ: Московский Политех
11.16 ЗАДАНИЕ Д-5
Теорема об изменении кинетической энергии механической системы
Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывается трение скольжения тела А и сопротивление качению тела D, катящегося без скольжения. Другими силами сопротивления и массами нерастяжимых нитей пренебрегаем. Требуется определить скорость и ускорение тела А в тот момент, когда оно пройдет путь SA = S.
В задаче обозначено:
mA, mB, mD, mE — массы тел A, B, D, E;
RB, rB, RD, rD, RE, rE — радиусы больших и малых окружностей тел B, D, E;
ρB, ρD, ρE — радиусы инерции тел В, D, Е относительно горизонтальных осей, проходящих через их центры тяжести;
α — угол наклона плоскости к горизонту;
f — коэффициент трения скольжения тела А;
k — коэффициент трения качения тела D.
Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами. Наклонные участки нитей параллельны соответствующим наклонным плоскостям.
Считать величину m равной 10 кг, g = 10 м/с².
Таблица Д-5
| № варианта | № рисунка | mА, кг | mВ, кг | mЕ, кг | mD, кг |
| 6 | 6 | 9m | 8m | 3m | 3m |
Продолжение таблицы Д-6
| RВ, м | rВ, м | ρВ, м | RD, м | rD, м | ρD, м | α,º | k, см | S, м |
| 0,8 | 0,5 | 0,7 | 0,9 | 0,3 | 0,5 | 20 | 0,4 | 1,5 |
ВУЗ: Московский Политех
12.14 ЗАДАНИЕ Д-6
Принцип Даламбера для механической системы
Вертикальный вал вращается с постоянной угловой скоростью ω (рис.6.1). Вал, стержни 1, 2, 3 и точечный груз 4 лежат в одной плоскости и жестко скреплены между собой. Стержни имеют линейные плотности γ1, γ2, γ3 и длины l1, l2, l3, масса точечного груза равна m4. Определить указанные в таблице параметры конструкции так, чтобы в подпятнике А и подшипнике В не возникало динамических реакций. Исходные данные и определяемые величины приведены в таблице Д-6.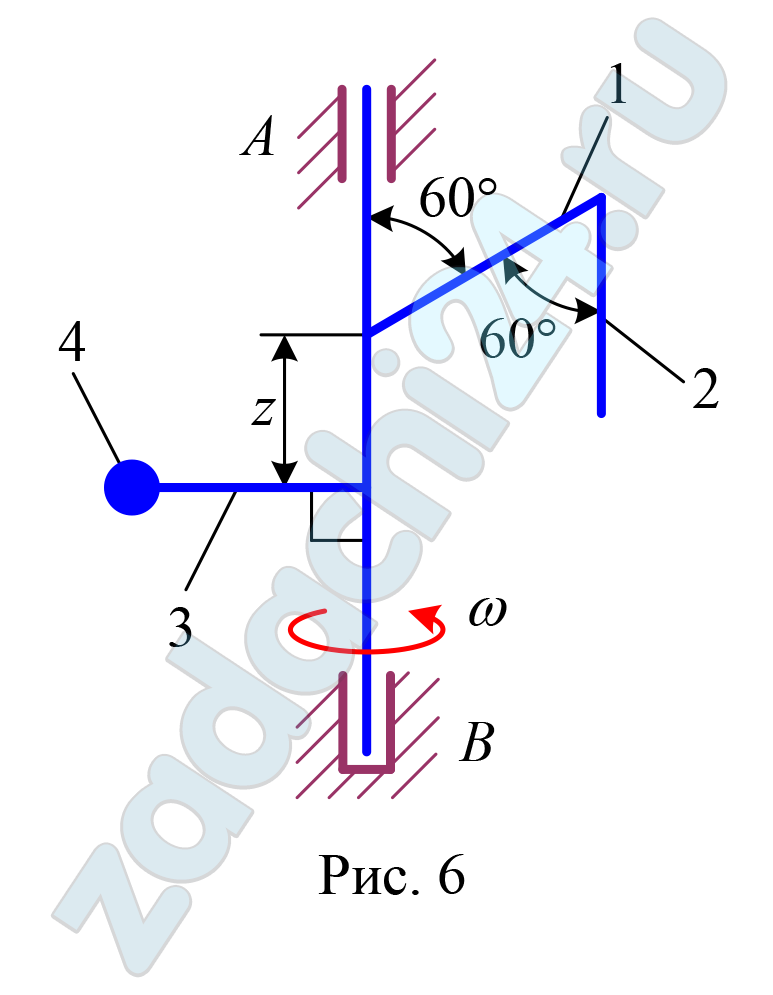
Таблица Д-6
| № варианта 6 | ||||||||
| № рис. | γ1,
кг/м |
γ2,
кг/м |
γ3,
кг/м |
m4,
кг |
l1,
м |
l2,
м |
l3,
м |
Найти |
| 6 | 5 | 6 | — | 10 | 6 | 2 | 3 | z, γ3 |
ВУЗ: Московский Политех
13.8 ЗАДАНИЕ Д-7
Принцип возможных перемещений
Механизмы (рис.7.1-7.3) в заданном положении находятся в равновесии. Необходимо определить величину, указанную в предпоследней графе таблицы Д-7.1, применяя принцип возможных перемещений и пренебрегая силами трения. Все необходимые для решения данные приведены в таблице Д-7.1.
Примечание: механизмы в вариантах 3, 6, 10, 14, 16, 18, 19, 25 и 30 расположены в вертикальной плоскости, а остальные — в горизонтальной.
Таблица Д-7.1
| № варианта | Линейный
размеры, см |
Сила Q, Н | Определить | Примечания |
| 6 | r1 = 15;
r2 = 50; r3 = 20; О1А = 80 |
200 | Р | О1А — невесомый |
ВУЗ: Московский Политех
14.3 ЗАДАНИЕ Д-8
Общее уравнение динамики
Механическая система, состоящая из груза 1 весом Р1, блоков 2 и 3 весом Р2 и Р3 соответственно и сплошного катка 4 весом Р4, движется под действием сил тяжести. Радиус инерции блоков 2 и 3 — ρ2 и ρ3. Если в таблице радиус инерции блока не указан, блок следует считать полым цилиндром. Каток 4 движется по рельсу, наклоненному к горизонту под углом α без скольжения. Коэффициент трения качения k. Трением в осях пренебречь, проскальзывание невесомых нерастяжимых нитей отсутствует. С помощью общего уравнения динамики определить ускорение оси катка. Схемы механизмов приведены на рис. 8.1, 8.2, данные – в таблице Д-8.1.
Таблица Д-8
| № варианта | № рисунка | Р1, кН | Р2, кН | Р3, кН | Р4, кН | α,º |
| 6 | 6 | 1 | 2 | 1 | 0,5 | 15 |
Продолжение таблицы Д-8
| R2, м | r2, м | ρ2, м | R3, м | r3, м | ρ3, м | R4, м | ρ4, м | r4, м | k, см |
| — | — | — | 0,4 | 0,2 | 0,3 | — | — | 0,2 | 0,5 |
ВУЗ: Московский Политех
16.1 ЗАДАНИЕ Д-9
Уравнения Лагранжа II рода
Для заданной механической системы на основе уравнений Лагранжа II рода составить дифференциальные уравнения движения. Необходимые данные и рекомендуемые обобщенные координаты приведены в таблице Д-9.
При решении задачи массами нитей пренебречь. Считать, что качение происходит без проскальзывания. Блоки и катки, для которых в таблице радиусы инерции не указаны, считать сплошными однородными цилиндрами. Силы сопротивления в подшипниках не учитывать. Заданные силы P и моменты пар M считать постоянными величинами.
Таблица Д-9
| № варианта | № рисунка | m1 | m2 | m3 | m4 | m5 | Р |
| 6 | 6 | m1 | m2 | m3 | m4 | m5 | — |
Продолжение Таблицы Д-9
| М | f | k | q1 | q2 | ρ | α | Дополнительные указания |
| — | — | — | x | ξ | 2r | — | ρ – радиус инерции тела 3 |
ВУЗ: Московский Политех