Теоретическая механика ИРНИТУ
2.52 Изучение равновесия плоской конструкции
На схемах (Рис. С1.0 ÷ С1.9) представлены по три способа закрепления конструкции, состоящей из двух прямолинейных стержней, жестко скрепленных между собой в точке С. Задаваемая нагрузка и размеры во всех трех случаях одинаковы. На каждую конструкцию действует пара сил с моментом М = 50 кН∙м, распределенная нагрузка интенсивности q = 10 кН/м и одна сосредоточенная сила. Величина этой силы, ее направление и точка приложения указаны в табл. С1. Там же в столбце «Нагруженный участок» указано, на каком участке действует распределенная нагрузка. Направление распределенной нагрузки на различных по расположению участках указано в табл. С1А. При расчетах заданный на рисунках размер «а» принять равным 0,5 м.
- Определить реакции опор для способа закрепления конструкции на схеме а).
- Среди двух оставшихся схем б) и в) определить, в какой из них полная величина реакции в виде силы в точке А (рис. С1.0, С1.1, С1.2, С1.3, С1.4) или в точке В (рис. С1.5, С1.6, С1.7, С1.8, С1.9) имеет наименьший модуль и для выбранной схемы найти все остальные реакции.

Таблица С1
Действующие нагрузки
| Сила | 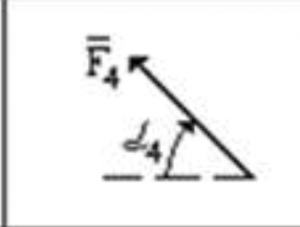 |
Нагруженный участок | |
| F4 = 40 кН | |||
| Номер условия | Точка приложения | α, град | |
| 1 | E | 45 | AD |
Таблица С1а
Направление распределенной нагрузки
ВУЗ: ИРНИТУ
2.73 Исследование равновесия конструкции
Конструкция, состоящая из двух прямолинейных стержней, жестко скрепленных между собой в точке С, расположена в вертикальной плоскости. На конструкцию действует пара сил с моментом М = 50 кН∙м, равномерно распределенная нагрузка интенсивности q = 10 кН/м и одна сосредоточенная сила. Величина этой силы, ее направление и точка приложения указаны в табл. С1. Там же в столбце «Нагруженный участок» указано, на каком участке действует распределенная нагрузка. Направление распределенной нагрузки на различных по расположению участках указано в табл. С1 А. При расчетах размер а принять равным а = 0,5 м.
Для данной конструкции
- определить реакции связей конструкции для приведенных в условии данных;
- выполнить проверку правильности определения реакций.
 Таблица С1
Таблица С1
Действующие нагрузки
| Сила |  |
Нагруженный участок | |
| F1 = 10 кН | |||
| Номер условия | Точка приложения | α, град | |
| 0 | К | 60 | СЕ |
Таблица С1А
Направление распределенной нагрузки
Скачать файл (банки РФ) 250 RUB
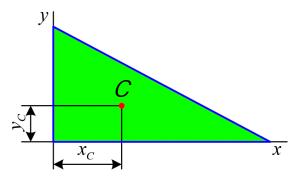
5.7 Определение координат центра тяжести тела
Две однородные прямоугольные пластины, приваренные под прямым углом друг к другу, образуют угольник. Размеры пластин в направлениях, параллельных координатным осям Х, Y, Z, равны соответственно или 2l, 3l и l на рис. С3.0 ÷ С3.4), или 2l, 3l и 4l на рис. С3.5÷С3.9). Силы тяжести большей и меньшей пластин на рис. С3.0 ÷ С3.4 соответственно равны 10 кН и 4 кН, для рис. С3.5 ÷ С3.9 силы тяжести пластин одинаковы и равны 8 кН. Каждая из пластин расположена параллельно одной из координатных плоскостей (плоскость ХАY горизонтальна).
Из одной из пластин угольника вырезана фигура, расположение и вид которой указаны в таблице С2. Точки, обозначенные на рисунках, находятся по краям или в серединах сторон пластин.
Вычислить координаты центра тяжести угольника с вырезом для указанных на рисунках систем координат. При расчетах принять l = 0,5 м. Толщиной пластин пренебречь.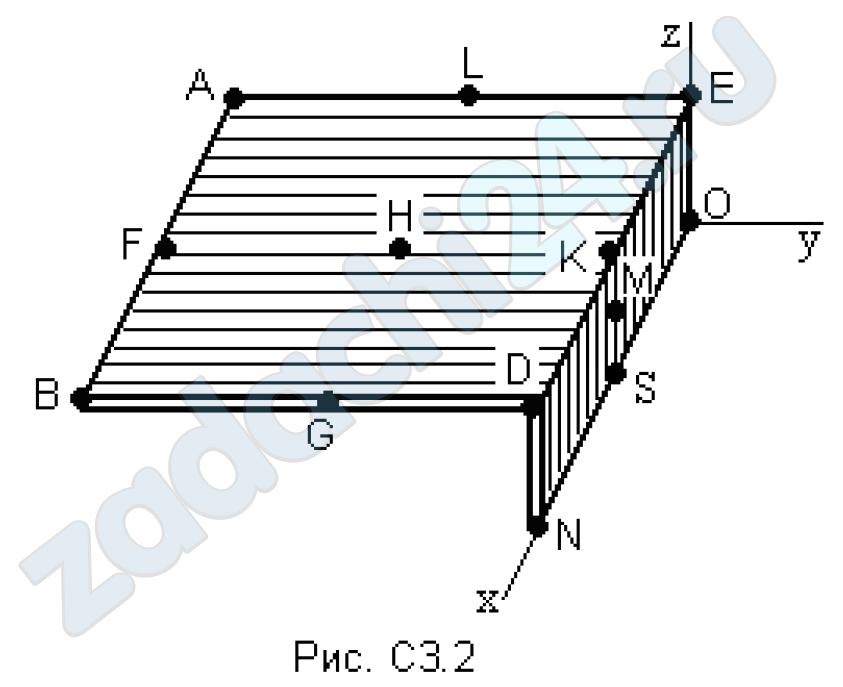
Таблица С2
| № варианта | Вырезаемое тело | |
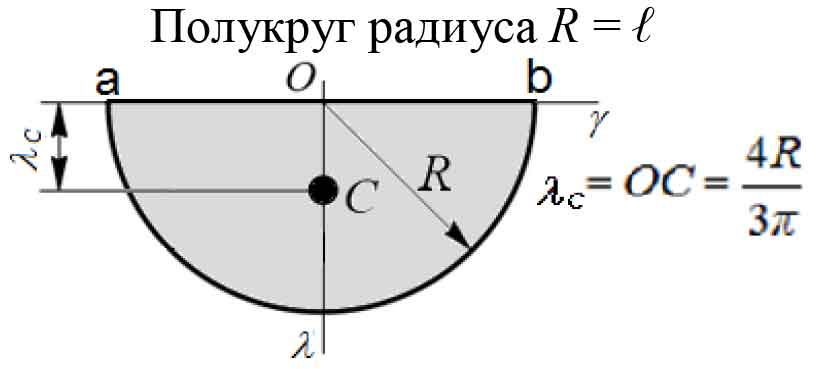 |
||
| прямая аОb
полукруга расположена вдоль стороны угольника |
точка пластины,
из которой начинается построение прямой аОb полукруга |
|
| 0 | BGD | B |
5.6 Определение координат центра тяжести тела
Две однородные прямоугольные пластины, приваренные под прямым углом друг к другу, образуют угольник. Размеры пластин в направлениях, параллельных координатным осям х, у, z, равны соответственно или 2l, 3l и l (рис. С2.0 ÷ С2.4), или 2l, 3l и 4l (рис. С2.5÷С2.9). Силы тяжести большей и меньшей пластин (рис. С2.0 ÷ С2.4) соответственно равны 10 кН и 4 кН, для рис. С2.5 ÷ С2.9 силы тяжести пластин одинаковы и равны 8 кН. Каждая из пластин расположена параллельно одной из координатных плоскостей (плоскость хАу горизонтальная).
Из одной из пластин угольника вырезана фигура, расположение и вид которой указаны в таблице С2. Точки, обозначенные на рисунках, находятся по краям или в серединах сторон пластин.
Вычислить координаты центра тяжести угольника с вырезом для указанных на рисунках систем координат. При расчетах принять l = 0,5 м. Толщиной пластин пренебречь.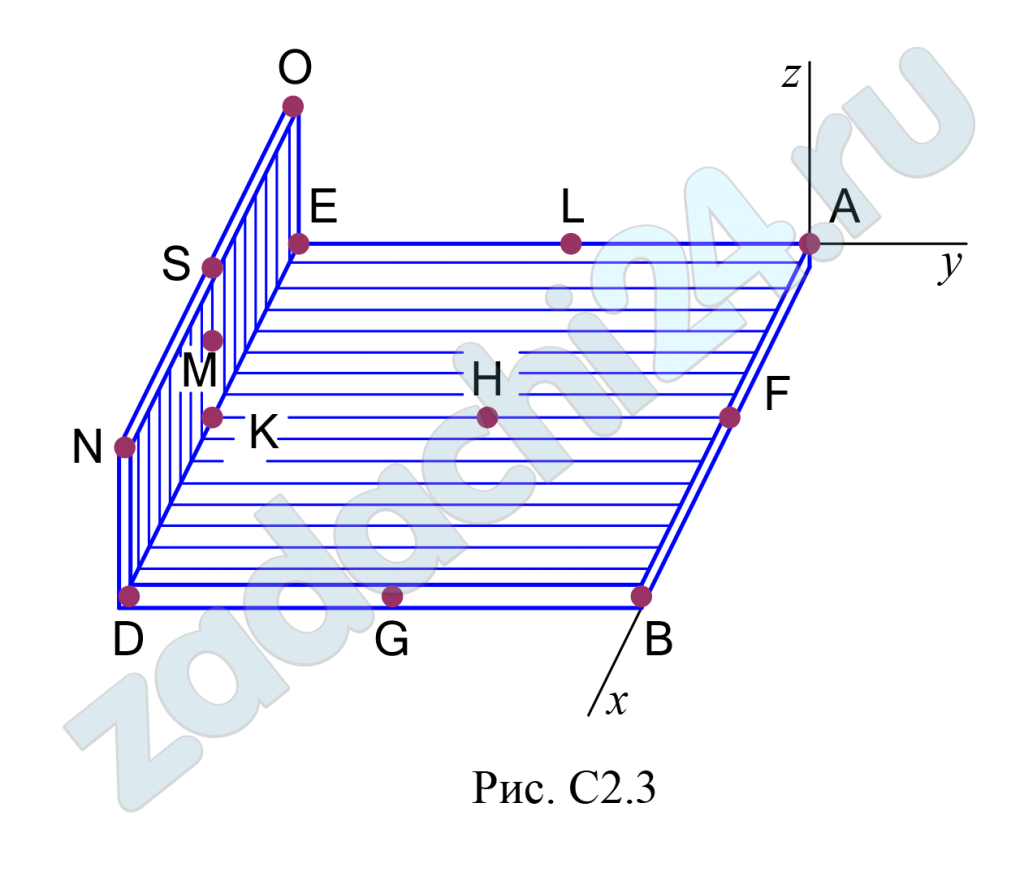
Таблица С2
Расположение и вид вырезаемой фигуры
| № варианта | Вырезаемое тело |
| Треугольник | |
| 1 | ALF |
ВУЗ: ИРНИТУ
6.17 Задание К1. Определение кинематических характеристик движения материальной точки
По заданным уравнениям движения точки x = f1(t), y = f2(t) найти уравнение траектории ее движения, и для момента времени t1 = 1с вычислить ее скорость, нормальное, касательное и полное ускорения, а также радиус кривизны траектории. На рисунке в масштабе изобразить траекторию движения точки и для заданного момента времени t1 = 1с построить векторы скорости и ускорения.
Уравнения движения точки x = f1(t) указаны на соответствующих рисунках, а уравнения движения y = f2(t) приведены в табл. К1 (для рис. 0-2 – в столбце 2, для рис. 3-6 − в столбце 3, для рис. 7-9 – в столбце 4); величины х и у измеряются в см, время в секундах (с).
Таблица К1
Уравнения движения точки y = f2(t)
| Номер условия | y = f2(t) |
| рис. 0, 1, 2 | |
| 0 | 3 – 4cos(πt/4) |
6.3 Определение кинематических характеристик движения материальной точки
По заданным уравнениям движения точки x = f1(t), y = f2(t) найти уравнение траектории точки. Для момента времени t1 = 1с вычислить ее скорость, нормальное, касательное и полное ускорения, а также радиус кривизны траектории. На рисунке в масштабе изобразить траекторию движения точки и для заданного момента времени t1 = 1с построить векторы скорости и ускорения.
Уравнения движения точки x = f1(t) указаны на соответствующих рисунках, а уравнения движения y = f2(t) приведены в табл. К1 (для рис. К1.0 ÷ К1.2 – в столбце 2, для рис. К1.3 ÷ К1.6 − в столбце 3, для рис. К1.7 ÷ К1.9 – в столбце 4); величины х и у измеряются в см, время в секундах.
Таблица К1
Уравнения движения точки y = f2(t)
| Номер условия | y = f2(t) |
| Рис. К1.3, К1.4, К1.5, К1.6 | |
| 1 | 1+3 sin² πt/6 |
ВУЗ: ИРНИТУ
7.22 Определение кинематических характеристик движения твердых тел
Плоский механизм, расположенный в вертикальной плоскости, состоит из стержней 1, 2, 3 катка 4 и ползуна 5, соединенных между собой и с неподвижной опорой O шарнирами (рис. K2.0 ÷ K2.9). Качение катка 4 происходит без скольжения и отрыва от плоскости. Длины стержней l1, l2, l3, радиус катка R4 и другие необходимые для расчета размеры указаны на рисунках. В некоторый момент времени положение движущегося механизма определяется углами α, β, γ, δ. Значения этих углов, а также величина угловой скорости ведущего звена или линейная скорость одной из точек механизма указаны в табл. K2.
Для данного положения механизма определить величины, указанные в таблице в столбце «Найти».
Таблица К2
Таблица исходных данных
| Номер условия | Углы в градусах | Дано | Найти | |||||
| α | β | γ | δ | ω1, с-1 | VB, м/c | VС, м/c | ||
| 0 | 60 | 135 | 90 | 30 | 2 | — | — | ω2, ω3, ω4, VА, VВ, VС |
7.3 Определение характеристик движения точек и тел плоского механизма
Плоский механизм, расположенный в вертикальной плоскости, состоит из стержней 1, 2, 3 катка 4 и ползуна 5, соединенных между собой и с неподвижной опорой O шарнирами (рис. K2.0 ÷ K2.9).
Качение катка 4 происходит без скольжения и отрыва от плоскости. Длины стержней l1, l2, l3, радиус катка R4 и другие необходимые для расчета размеры указаны на рисунках.
В некоторый момент времени положение движущегося механизма определяется углами α, β, γ, δ. Значения этих углов, а также величина угловой скорости ведущего звена или линейная скорость одной из точек механизма указаны в табл. K2.
Для данного положения механизма определить величины, указанные в таблице в столбце «Найти».
Таблица К2
Таблица исходных данных
| Номер условия 1 | |||||||
| Углы в градусах | Дано | Найти | |||||
| α | β | γ | δ | ω1, с-1 | VB, м/c | VС, м/c | |
| 30 | 90 | 45 | 45 | — | -1 | — | ω1, ω2, ω3, ω4,
VА, VС |
ВУЗ: ИРНИТУ
15.1 Интегрирование дифференциальных уравнений движения точки, находящейся под действием постоянных сил
Груз М массой m начинает движение из точки D с начальной скоростью V0. Его движение происходит по наклонной плоскости длины l, составляющей угол α с горизонтом вдоль линии АВ наибольшего ската (рис. Д1.0 ÷ Д1.9). Положение точки D задается величиной AD = s0, вектор начальной скорости V0 направлен параллельно прямой АВ к точке В. При движении по плоскости на груз действует постоянная сила Q, направление которой задается углом γ; коэффициент трения скольжения между грузом и наклонной плоскостью равен f. Через τ с груз покидает плоскость или в точке A, или в точке B и, двигаясь далее в вертикальной плоскости под действием только силы тяжести, через T секунд после отделения от плоскости попадает в точку С. Все возможные варианты траекторий движения груза в точку C показаны на рисунках.
Считая груз материальной точкой найти:
– точку (А или В) отрыва груза от плоскости;
– время τ движения груза по наклонной плоскости;
– скорость груза VB (или VA) в момент отрыва;
– координаты xC, yC точки C приземления груза;
– время T движения груза в воздухе;
– скорость VC груза в точке падения.
Таблица Д1
Исходные данные
| Номер условия | l, м | α,º | γ,º | m, кг | s0, м | V0, м/c | Q, Н |
| 1 | 50 | 45 | 30 | 20 | 15 | 15 | 30 |
Оформление готовой работы
ВУЗ: ИРНИТУ
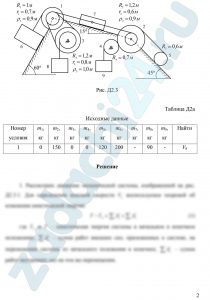
11.14 Применение теоремы об изменении кинетической энергии к изучению движения механической системы
Механическая система состоит из ступенчатых шкивов, колес, блоков 1÷5 и грузов 6÷9 (рис. Д2.0 ÷ Д2.9). На рисунках приняты обозначения: Rk – радиус внешней ступени шкива или радиус тела, rk – радиус внутренней ступени шкива, ρk – радиус инерции тела относительно оси вращения. Для тел 1,2,3 заданы радиусы инерции ρ1, ρ2, ρ3 относительно оси вращения, масса тела 4 равномерно распределена по внешнему ободу, тело 5 считать однородным цилиндром. Тела системы соединены друг с другом гибкими невесомыми нерастяжимыми нитями, которые или перекинуты через блоки, или намотаны на шкивы; участки нитей параллельны соответствующим плоскостям. Некоторые тела соединены ременными или фрикционными передачами.
Радиусы тел и радиусы инерции указаны на рис. Д2.0 ÷ Д2.9. Массы тел приведены в табл. Д2. Прочерк в таблице означает, что тело отсутствует и изображать его не надо. Если масса тела равна нулю, то данное тело показывается на рисунке, но его массой при расчетах следует пренебречь.
В некоторый момент времени под действием сил тяжести система приходит в движение из состояния покоя.
При скольжении по плоскостям на грузы действуют силы трения, коэффициент трения скольжения f равен 0,01. Качение всех тел происходит без скольжения; при этом для случая качения тел по неподвижным плоскостям следует учитывать трение качения, коэффициент трения качения δ = 1 см. Трением в осях вращения пренебречь. Длины нитей и длины участков достаточны для того, чтобы тела при движении не сталкивались друг с другом.
Определить скорость, указанную в табл. Д2 в столбце «Найти», после того как этот груз переместится на расстояние s = 10 м. При этом нужно указать, в какую сторону этот груз движется.
Таблица Д2а
Исходные данные
| Номер условия 1 | ||||
| m1, кг | m2, кг | m3, кг | m4, кг | m5, кг |
| 0 | 150 | 0 | 0 | 120 |
| m6, кг | m7, кг | m8, кг | m9, кг | Найти |
| 200 | — | 90 | — | V8 |
Оформление готовой работы
ВУЗ: ИРНИТУ