Суров Г.Я. Гидравлика и гидропривод в примерах и задачах Архангельск: Северный (Арктический) федеральный университет
6.27 Определить диаметр d сосуда, наполненного водой и вращающегося с постоянной угловой скоростью ω=10 с-1, чтобы разность уровней у стенки и в низшей точке свободной поверхности не превышала Δh=0,86 м (рис. 6.31).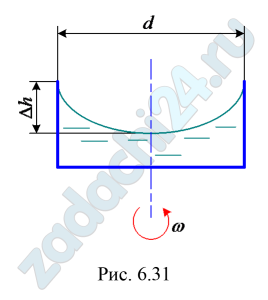
6.24 Сосуд диаметром d=0,60 м и высотой Н=1,5 м, наполненный водой до высоты h=1,0 м, вращается с постоянной угловой скоростью ω=10 с-1. Определить максимальное избыточное давление на дно сосуда (рис. 6.32).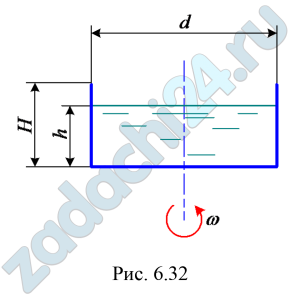
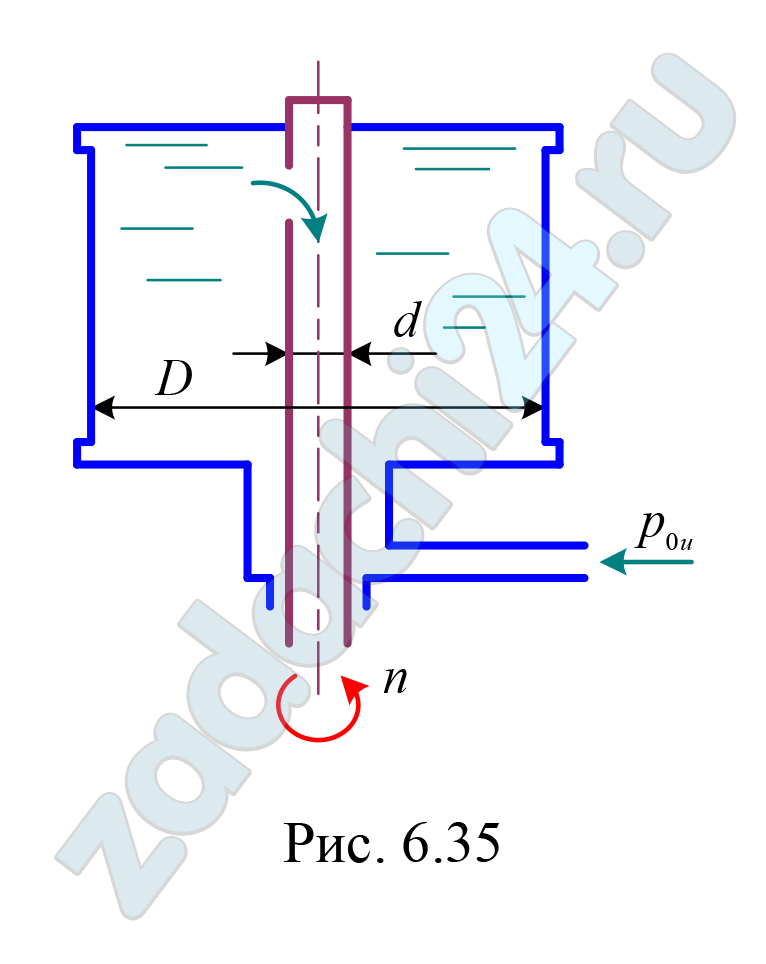
6.56 Ротор центрифуги, включенной в систему смазки двигателя внутреннего сгорания для очистки масла, представляет собой полый цилиндр, заполненный маслом (ρ = 900 кг/м³) и вращающийся с частотой n = 8000 об/мин (рис. 6.35). Определить давление масла на внутренней боковой поверхности ротора и силу давления на крышку ротора, если диаметры D = 120 мм, d = 30 мм. Масло подводится к центрифуге под давлением р0и = 0,5 МПа.
Скачать файл (банки РФ) 150 RUB)6.55 Цилиндрический сосуд диаметром D = 90 мм вращается на вертикальном валу диаметром d = 20 мм (рис. 6.36). Определить минимальную угловую скорость ω, при которой жидкость не соприкасается с валом, если первоначально сосуд был заполнен до уровня h = 0,06 м. Считать, что жидкость не поднимается до крышки сосуда.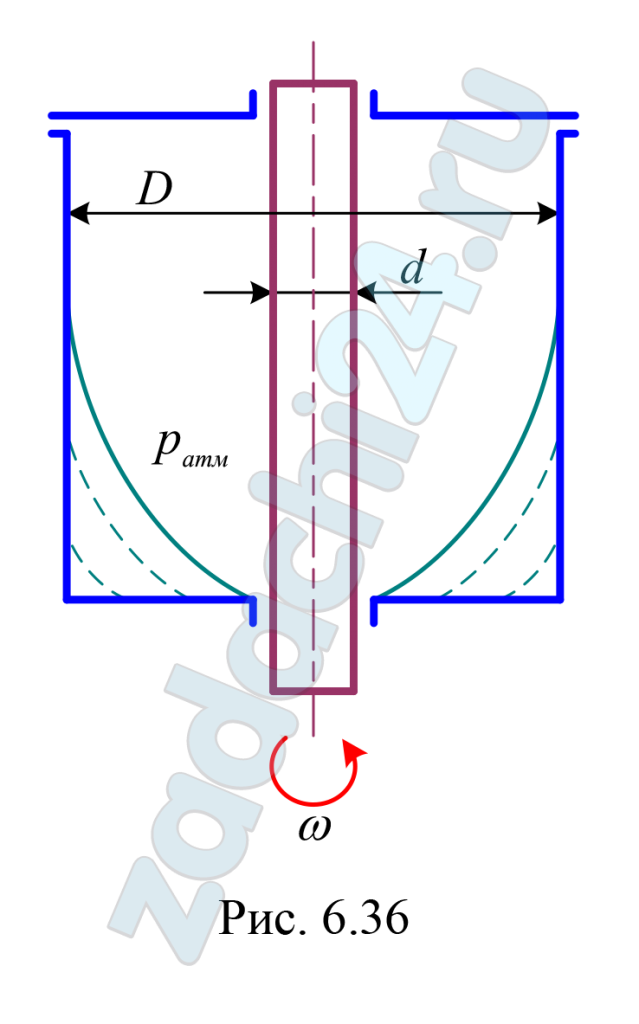
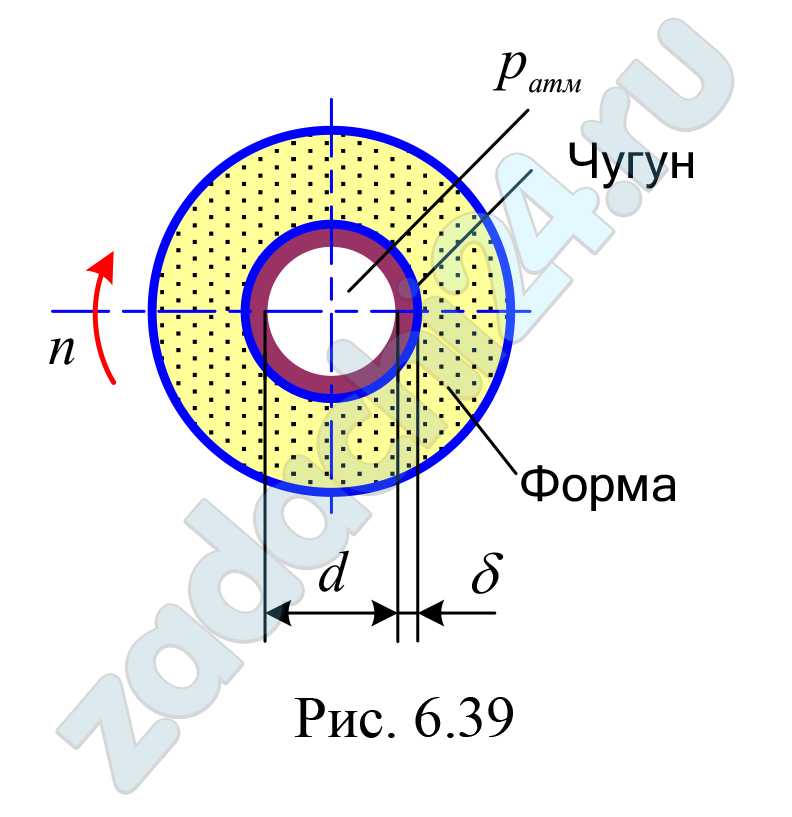
6.54 В форме, вращающейся вокруг горизонтальной оси, производится отливка чугунных труб внутренним диаметром d = 180 мм и толщиной стенки δ = 20 мм. Определить избыточное давление на внутренней поверхности формы при плотности чугуна ρ = 7000 кг/м³ и частоте вращения формы n = 1000 об/мин (рис. 6.39).
Скачать файл (банки РФ) 200 RUB)6.34 Внутри тормозного барабана с внутренним диаметром D = 380 мм и шириной b = 210 мм, вращающегося с частотой вращения n = 1000 об/мин, находится охлаждающая вода в объеме V = 6 л (рис. 6.40). Определить избыточное давление, оказываемое водой на внутреннюю поверхность барабана, если угловая скорость вращения воды равна угловой скорости вращения барабана.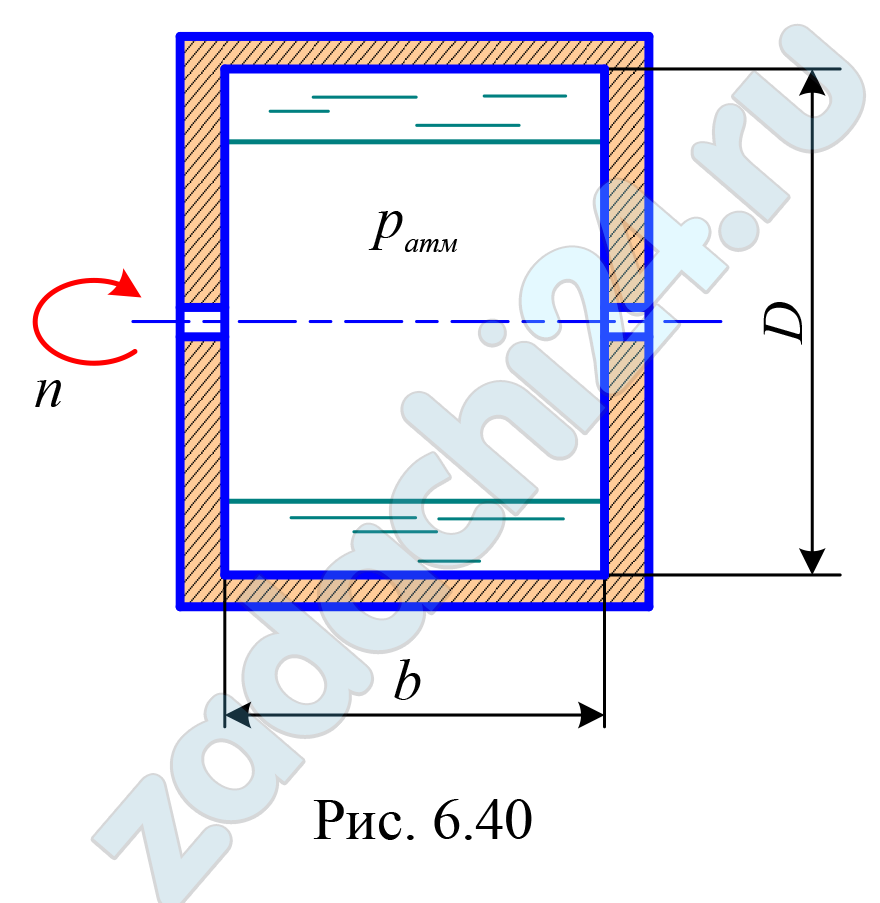
6.53 Цистерна, заполненная нефтью, движется на спуске с уклоном i = 0,2. Определить ускорение, при котором давление на торцовые поверхности будет одинаковым (рис. 6.11).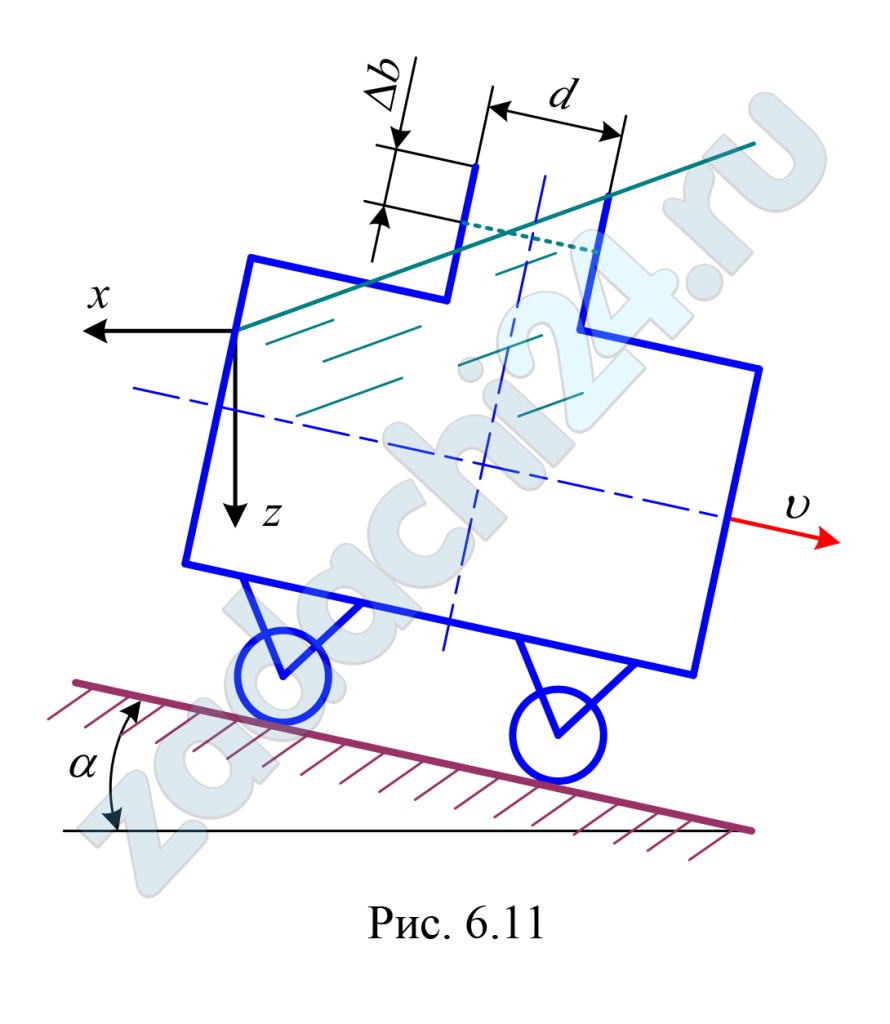
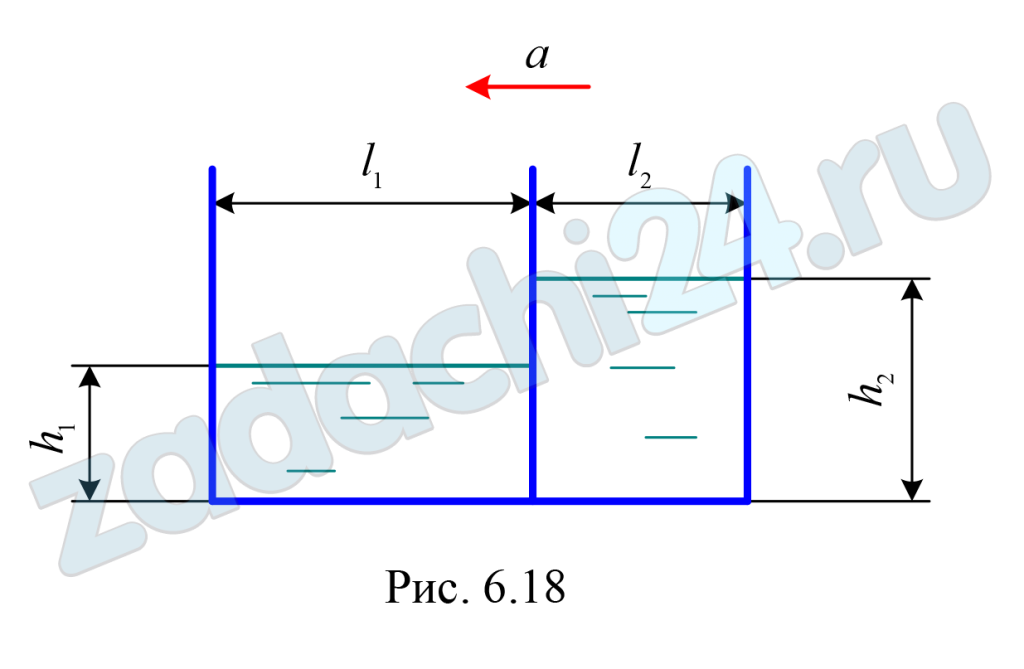
6.59 Призматический сосуд, перемещающийся горизонтально с постоянным ускорением, разделен плоской перегородкой на два отсека, заполненных одинаковой жидкостью до высот h1 = 1,0 м и h2 = 1,5 м. Определить ускорение, при котором суммарная сила давления воды на перегородку равна нулю (рис. 6.18).
Скачать файл (банки РФ) 220 RUB)6.41 Закрытый призматический сосуд длиной L = 2 м, перемещающийся горизонтально с постоянным ускорением a = 6 м/с², заполнен водой до высоты h = 0,5 м. Построить эпюру давления на дно сосуда, если высота сосуда Н = 1,0 м, а избыточное давление внутри сосуда р0и = 0,2·105 Па (рис. 6.19).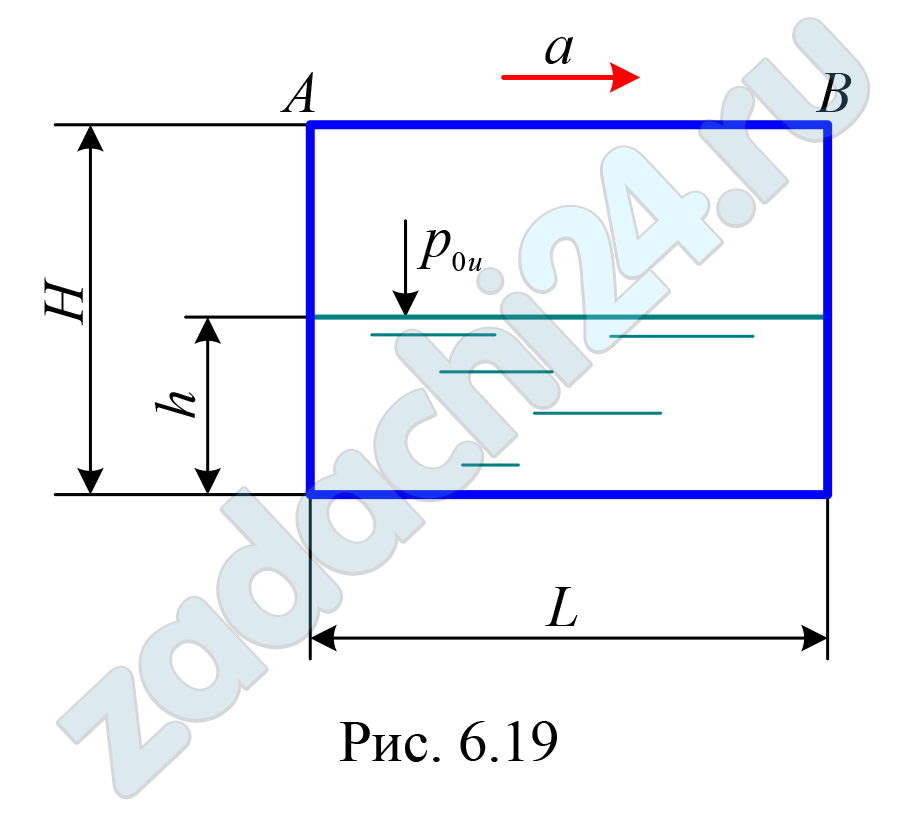
6.50 Определить ускорение, при котором сила давления воды на дно поднимаемого ведра будет равна Р = 160 Н, если диаметр ведра d = 0,2 м, а вода налита до высоты h = 0,4 м. При каком поступательном движении сила давления воды на дно будет равна нулю (рис. 6.21)?