Суров Г.Я. Гидравлика и гидропривод в примерах и задачах Архангельск: Северный (Арктический) федеральный университет
6.19 Закрытый призматический сосуд длиной L=2 м, высотой Н=1 м, шириной b=1 м, перемещающийся горизонтально с постоянным ускорением а=6 м/с², заполнен водой до высоты h=0,5 м. Определить силы давления на торцовые стенки А и В, если давление на свободной поверхности жидкости в сосуде р0и= 0,2·105 Па (рис. 6.19).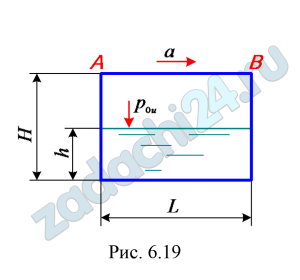
6.39 Автомобиль движется горизонтально с постоянным ускорением а = 4,0 м/с². Определить минимальный объем топлива в баке, обеспечивающий его подачу без подсоса воздуха, если длина бака L = 0,5 м, ширина b = 0,4 м, высота Н = 0,2 м, расстояние h = 10 мм (рис. 6.20). Считать, что бензопровод установлен в центре горизонтальной проекции бака, его диаметр мал по сравнению с длиной бака.
6.40 Определить силу давления воды на дно ведра, поднимаемого с ускорением а = 1 м/с², если диаметр ведра d = 0,2 м, вода налита до высоты h = 0,4 м (рис. 6.21).
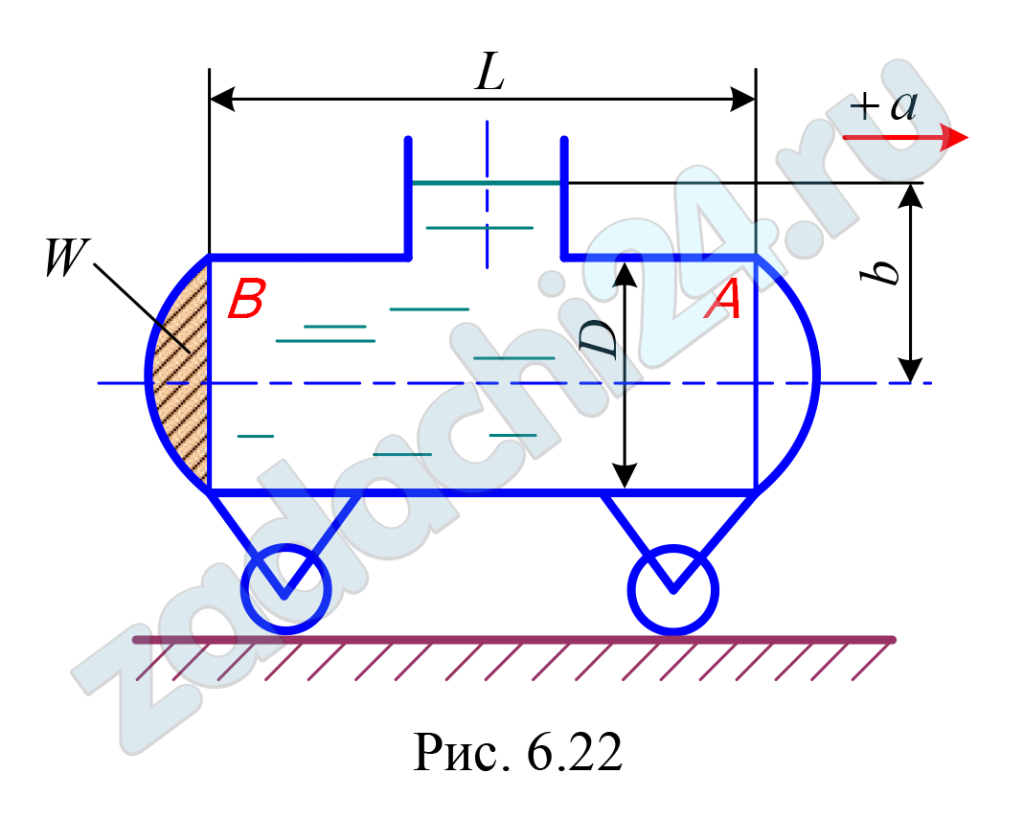
6.57 Цистерна диаметром D = 2,4 м и длиной L = 5,0 м, наполненная нефтью (относительная плотность δ = 0,9 ) до высоты b = 2 м, движется горизонтально с постоянным ускорением а = 2 м/с² (рис. 6.22). Определить силы давления на сферические крышки А и В цистерны, если объем (на рис. 6.22 заштрихован) V = 0,5 м. Ускорение свободного падения g = 10 м/с².
6.17 Определить расположение центра тяжести С бетонного раствора (hC и lC), залитого в закрытый кузов автомобиля, при его тормозном ускорении a=g (рис. 6.23). Считать, что кузов имеет форму параллелепипеда: L=2,88 м, Н=1,2 м, h=1,0 м.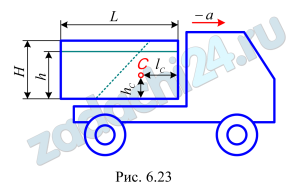
6.26 Цилиндрический сосуд, заполненный до высоты h=0,1 м жидкостью плотностью ρ=900 кг/м³, движется с ускорением а=g (рис. 6.25). Определить силы, действующие на крышки А и В, если L=1 м, D=0,5 м. Избыточное давление в горловине считать равным нулю, а расстояние l=0,1 м.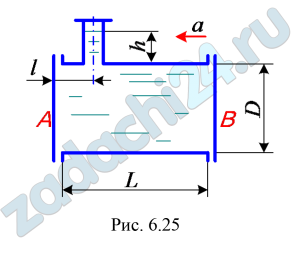
6.33 В кузов автомобиля-самосвала до уровня h = 0,48 м налит цементный раствор (рис. 6.26). Определить наименьший допустимый путь торможения самосвала от скорости υ = 36 км/ч до остановки из условия, что раствор не выплескивается из кузова. Считать кузов самосвала прямоугольным с размерами l = 3,0 м, Н = 0,96 м, а движение равнозамедленным.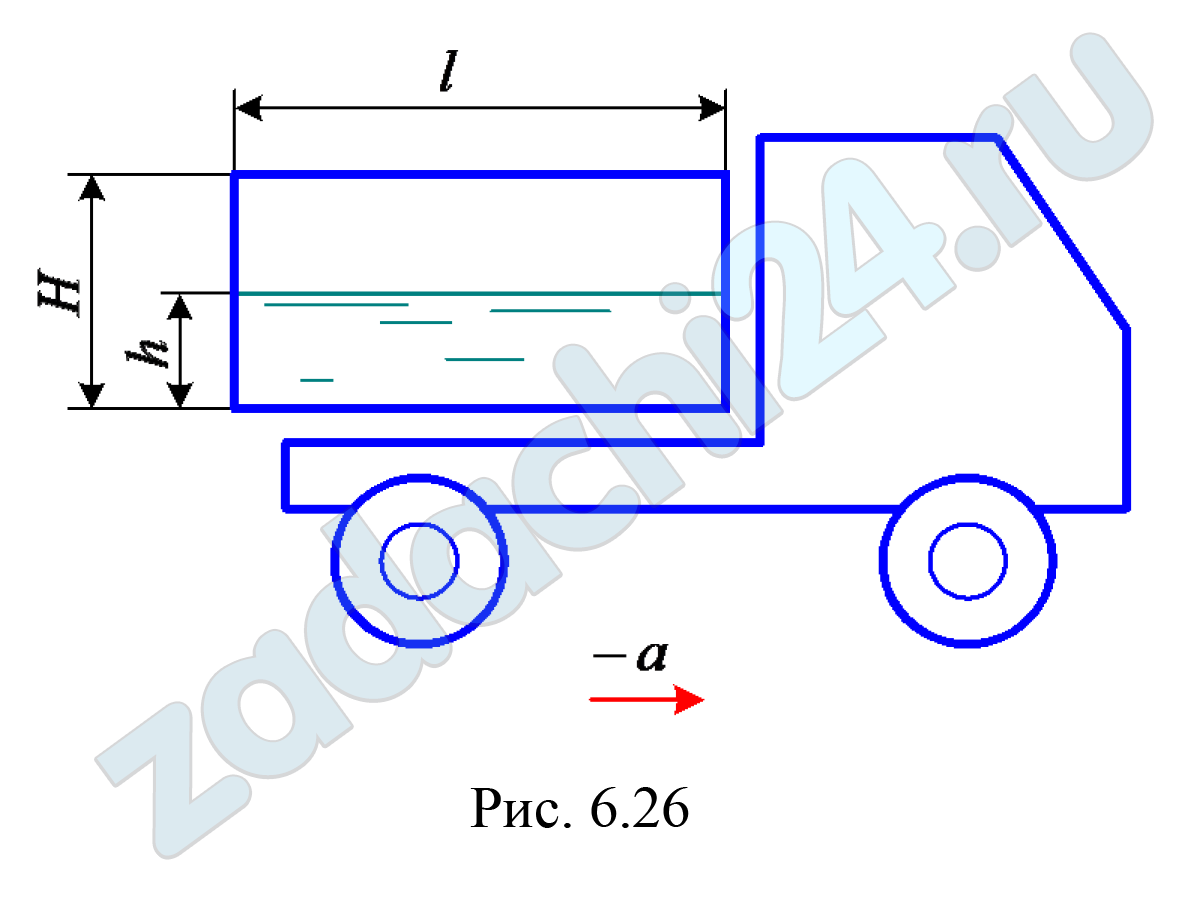
6.38 В сосуд высотой Н = 0,3 м залита жидкость до уровня h = 0,2 м. Определить, до какой угловой скорости можно раскрутить сосуд, с тем, чтобы жидкость не выплеснулась из него, если диаметр D = 100 мм (рис. 6.28).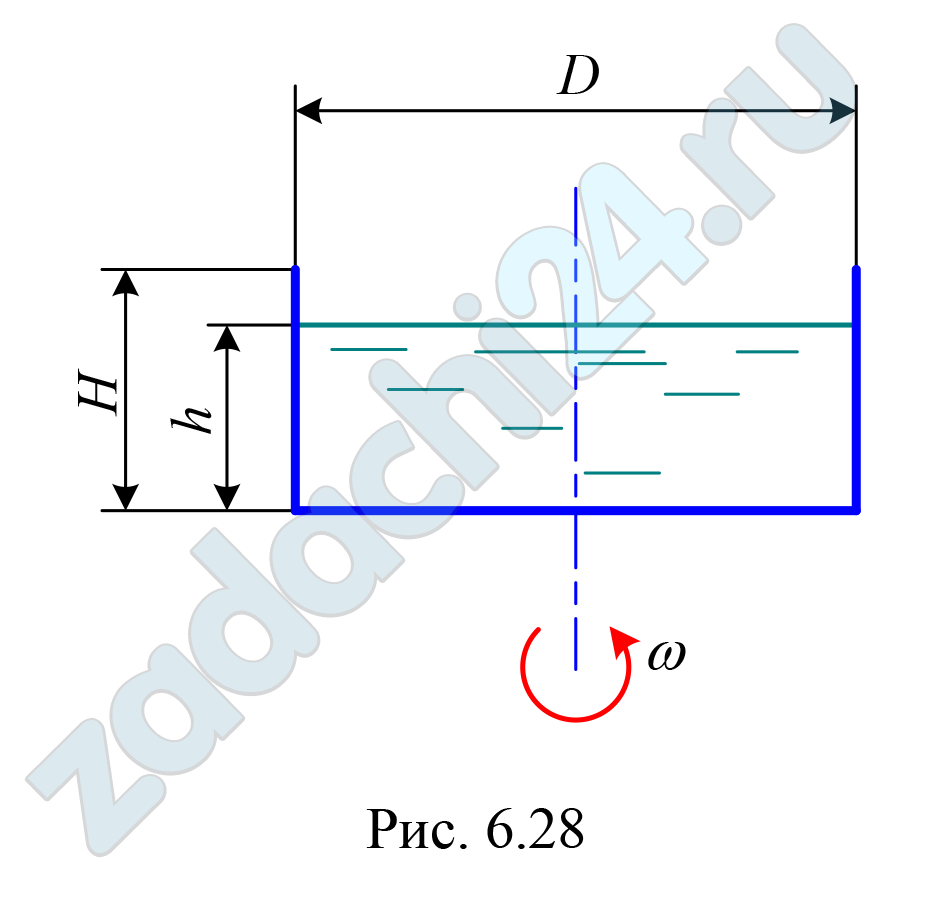
6.30 Определить минимальную частоту вращения n, которую нужно сообщить сосуду, изображенному на рис. 6.29, вокруг вертикальной оси для полного его опорожнения. Размеры: D = 240 мм, d = 120 мм, Н = 50 мм.
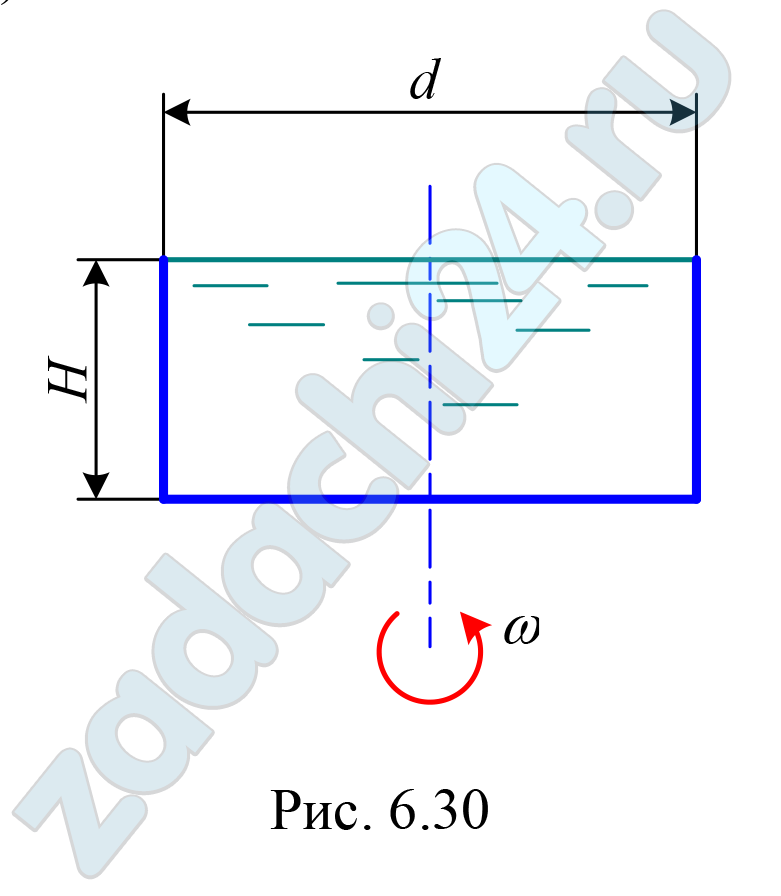
6.58 Определить, какой объем воды останется в открытом сосуде при вращении его с угловой скоростью ω = 10 с-1, если диаметр сосуда d = 0,60 м, а высота Н = 0,40 м (рис. 6.30).
