Рабинович О.М. Сборник задач по технической термодинамике

18.152 Для условий предыдущей задачи подсчитать расход топлива в случае, если вместо комбинированной выработки электрической и тепловой энергии на теплоэлектроцентрали будет осуществлена раздельная выработка электроэнергии в конденсационной установке и тепловой энергии в котельной низкого давления.

Конечное давление пара в конденсационной установке принять р₂=0,004МПа. К. п. д. котельной низкого давления принять тот же, что для котельной высокого давления.

Определить для обоих случаев коэффициент использования теплоты.

Ответ: В=6552 кг/ч, k_комбин=0,840, k_разд=0,589.

i-s диаграмма водяного пара с рассчитанным процессом прилагается к задаче

18.153 Для снабжения предприятия электрической и тепловой энергией запроектирована паротурбинная установка мощностью N=25000 кВт, работающая при следующих параметрах пара: р₁=9 МПа; t₁=480 ºС; р₂=1 МПа.

Весь пар из турбины направляется на производство и оттуда возвращается обратно в котельную в виде конденсата при температуре насыщения.

Считая, что установка работает по циклу Ренкина и при полной нагрузке, определить экономию, полученную вследствие комбинированной выработки электрической и тепловой энергии по сравнению с раздельной выработкой обоих видов энергии. Топливо, сжигаемое в котельной, имеет теплоту сгорания Q^р_н=25960 кДж/кг; к.п.д. котельной высокого и низкого давления принять одинаковыми и равными 0,83. Конечное давление пара в турбине при конденсационном режиме р₂=0,004 МПа.

Ответ: Э=23,1 %.

i-s диаграмма водяного пара с рассчитанным процессом прилагается к задаче

18.139 Турбина мощностью 6000 кВт работает при параметрах пара: р₁ = 3,5 МПа; t₁ = 435ºС; р₂ = 0,004 МПа.

Для подогрева питательной воды из турбины отбирается пар при р = 0,12 МПа (рис. 102).

Определить термический к.п.д. установки, удельный расход пара и теплоту и улучшение термического к.п.д. в сравнении с такой же установкой, но работающей без регенеративного подогрева.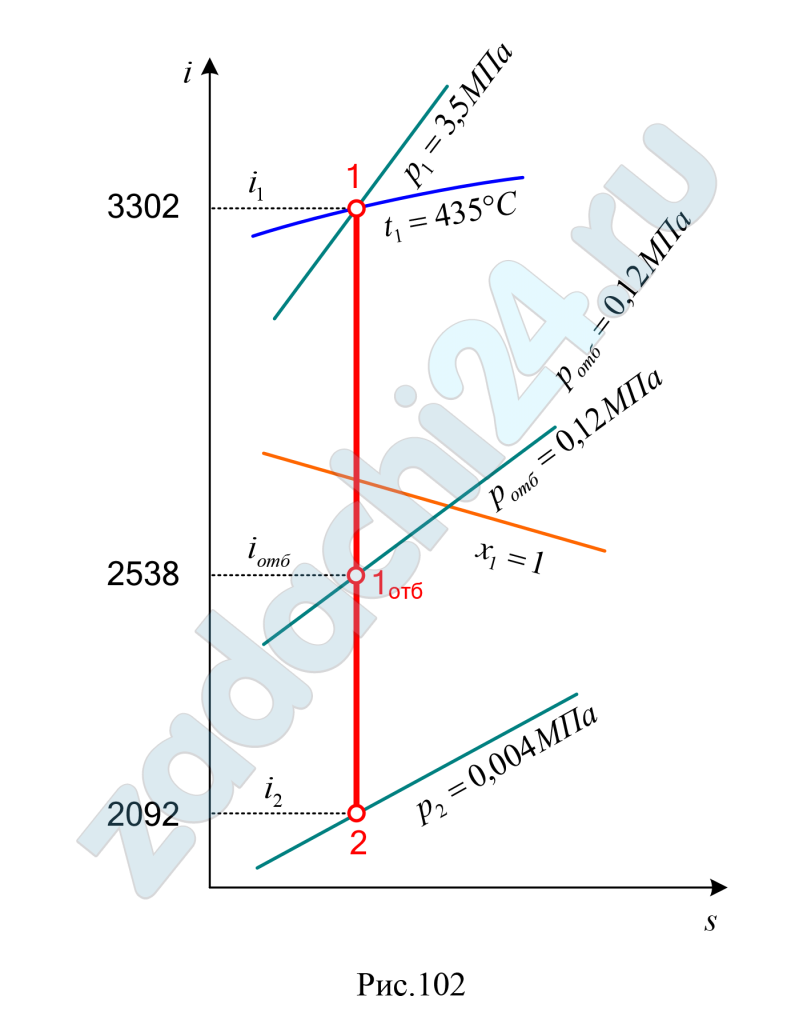

Ответ: η_tрег = 0,40; d_ор = 3,12 кг/(кВт·ч); q_ор = 8938 кДж/( кВт·ч); улучшение термического к.п.д. вследствие регенерации составит 5,26%.

18.55 Турбина мощностью 24 МВт работает при параметрах пара: р₁=2,6 МПа, t₁=420 ºC, р₂=0,004 МПа. Для подогрева питательной воды из турбины отбирается пар при р₀=0,12 МПа.

Определить термический к.п.д. и удельный расход пара. Определить также улучшение термического к.п.д. в сравнении с той же установкой, но работающей без регенеративного подогрева.

Ответ: η_tp=0,38, d_op=3,32 кг/(кВт·ч), η_t=0,361, Δη/η100=5,26%.

18.138 Из паровой турбины мощностью N = 25000 кВт, работающей при р₁ = 9 МПа, t₁ = 480ºС, р₂ = 0,004 МПа, производится два отбора: один при р_отб1 = 1 МПа и другой при р_отб2 = 0,12 МПа (рис. 103).

Определить термический к.п.д. установки, улучшение термического к.п.д. по сравнению с циклом Ренкина и часовой расход пара через каждый отбор.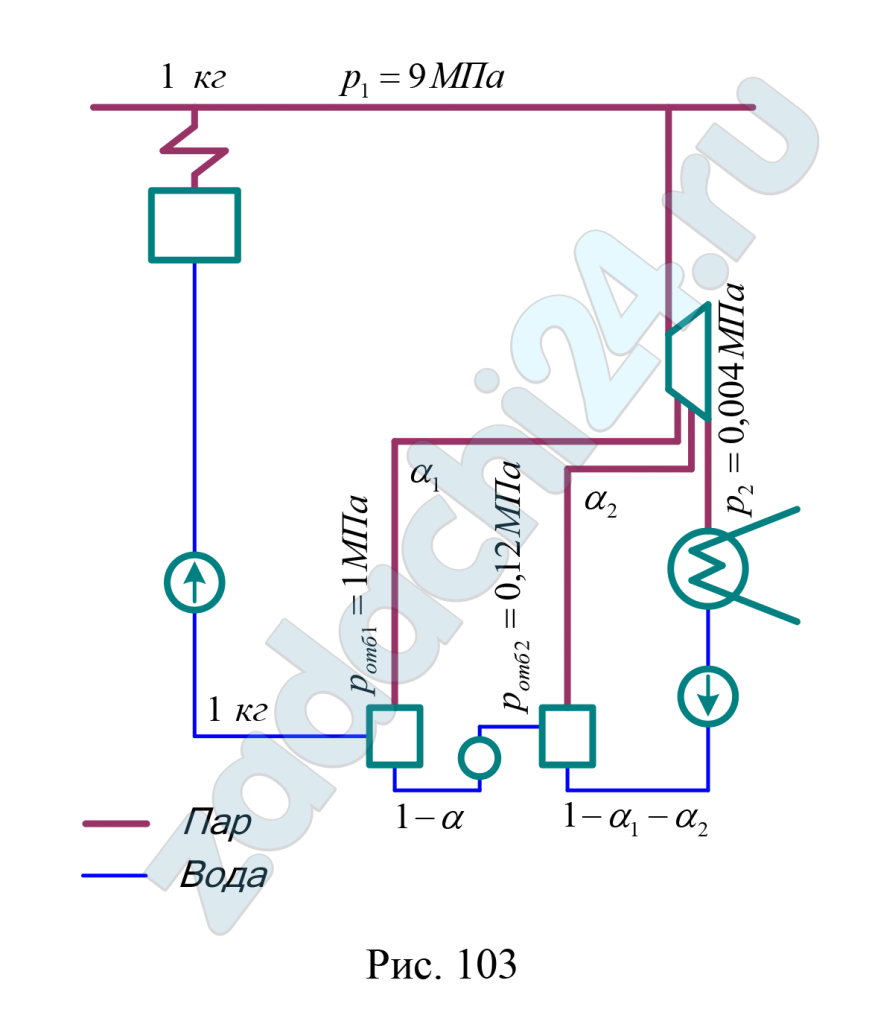

Ответ: D_отб1 = 10420 кг/ч, D_отб2 = 8985 кг/ч, η_tp = 0,464, улучшение термического к.п.д. регенеративного цикла по сравнению с циклом без регенерации составляет 10,2%.

is — диаграмма водяного пара с рассчитанным процессом прилагается к задаче

18.170 Паро-ртутная турбина мощностью 10000 кВт работает при следующих параметрах: р_Hg1 = 0,8 МПа; пар – сухой насыщенный; р_Hg2 = 0,01 МПа. Получающийся в конденсаторе – испарителе ртутной турбины сухой насыщенный водяной пар поступает в пароперегреватель, где его температура повышается до 450ºС, и затем направляется в пароводяную турбину, работающую при конечном давлении р₂ = 0,004 МПа.

Определить термический к.п.д. бинарного цикла, термический к.п.д. пароводяной турбины, улучшение к.п.д. от применения бинарного цикла, а также мощность пароводяной турбины.

Ответ: η_tб = 0,553; η_tН2О = 0,385; улучшение к.п.д. от применения бинарного цикла 43,6%; N_Н2О = 12260 кВт.

21.49 В компрессор воздушной холодильной установки поступает воздух из холодильной камеры давлением р=0,1 МПа и температурой t₁=-10 ºC. Адиабатно сжатый в компрессоре воздух до давления р₁=0,5 МПа направляется в охладитель, где он при p=const снижает свою температуру до t₃=+10 ºC. Отсюда воздух поступает в расширительный цилиндр, где расширяется по адиабате до первоначального давления, после чего возвращается в холодильную камеру. Отнимая теплоту от охлаждаемых тел, воздух нагревается до t₁=-10 ºC и вновь поступает в компрессор.

Определить температуру воздуха, поступающего в холодильную камеру, теоретическую работу, затрачиваемую в цикле. холодопроизводительность воздуха и холодильный коэффициент для данной установки и для установки, работающей по циклу Карно для того же интервала температур.

Ответ: t₄=-94 ºC, l₀=49,6 кДж/кг, q₀=85 кДж/кг, ε=1,71, ε_К=13,15.

21.3 Холодопроизводительность воздушной холодильной установки Q=83,7 МДж/ч. Определить ее холодильный коэффициент и потребляемую теоретическую мощность двигателя, если известно, что максимальное давление воздуха в установке р₂=0,5 МПа, минимальное давление р₁=0,11 МПа, температура воздуха в начале сжатия t₁=0ºC, а при выходе из охладителя t₃=20ºC. Сжатие и расширение воздуха принять политропными с показателем политропы n=1,28.

Ответ: ε=2,56, N_дв=9,1 кВт.

21.53 На рис. 117 представлена схема, а на рис. 118 изображен цикл паровой компрессорной холодильной установки. Пар аммиака при температуре t₁ = -10ºС поступает в компрессор В, где адиабатно сжимается до давления, при котором его температура t₂ = 20ºС, а сухость пара х₂ = 1. Из компрессора аммиак поступает в конденсатор С, где при постоянном давлении обращается в жидкость (х₃ = 0), после чего в особом расширительном цилиндре D адиабатно расширяется до температуры t₄ = -10ºС; при этой же температуре аммиак поступает в охлаждаемое помещение А, где, забирая теплоту от охлаждаемых тел, он испаряется, образуя влажный пар со степенью сухости х₁.

Определить холодопроизводительность аммиака, тепловую нагрузку конденсатора, работу, затраченную в цикле, и холодильный коэффициент.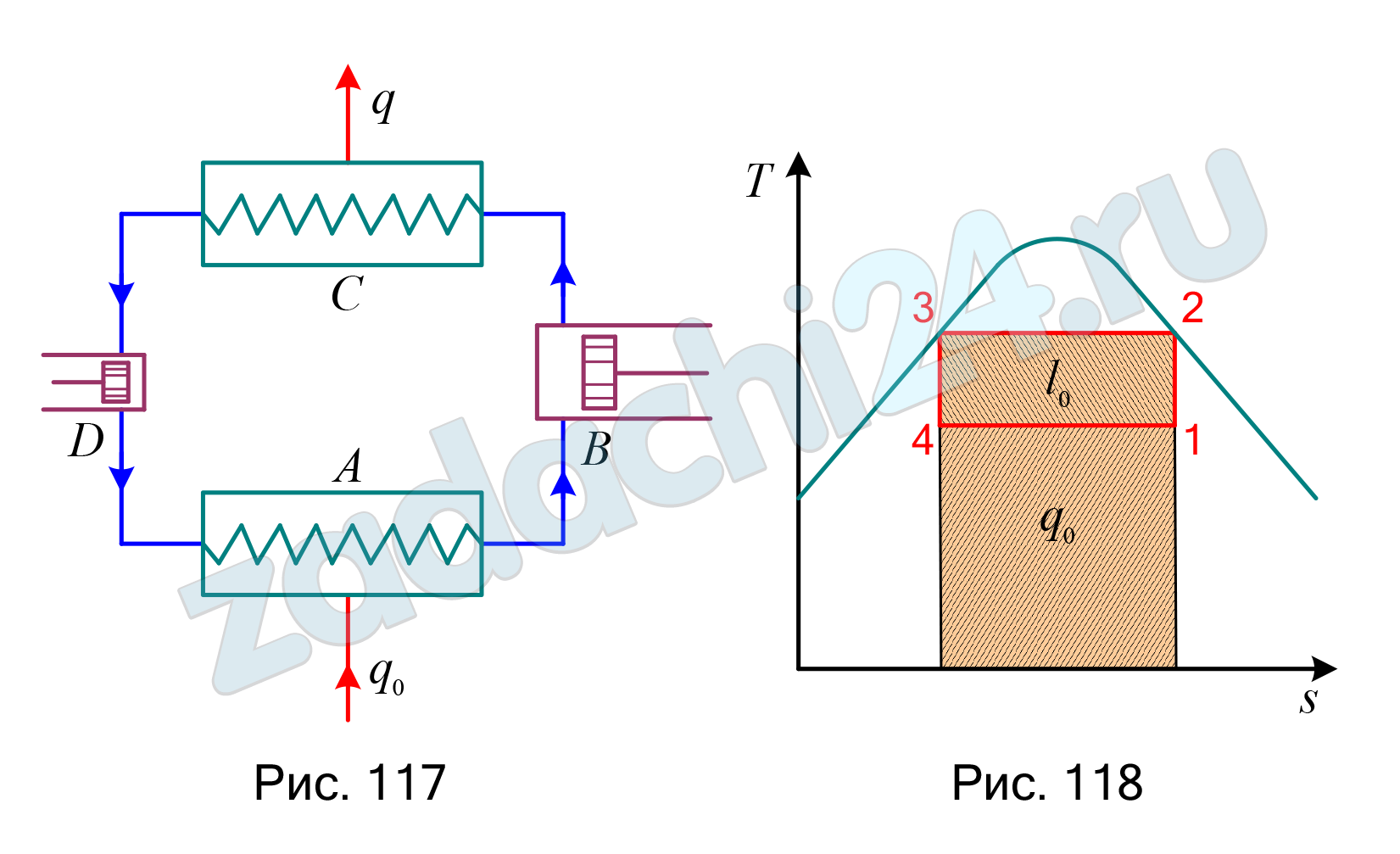

Ответ: q₀ = 1067,8 кДж/кг, q = 1186,9 кДж/кг, l₀ = 119,1 кДж/кг, ε = 8,96.

21.52 В схеме аммиачной холодильной установки, приведенной в предыдущей задаче, расширительный цилиндр заменяется редукционным вентилем. Новая схема представлен на рис. 109. В остальном все условия предыдущей задачи сохраняются.

Определить новое значение холодильного коэффициента εʹ и сравнить его с ε для схемы с расширительным цилиндром.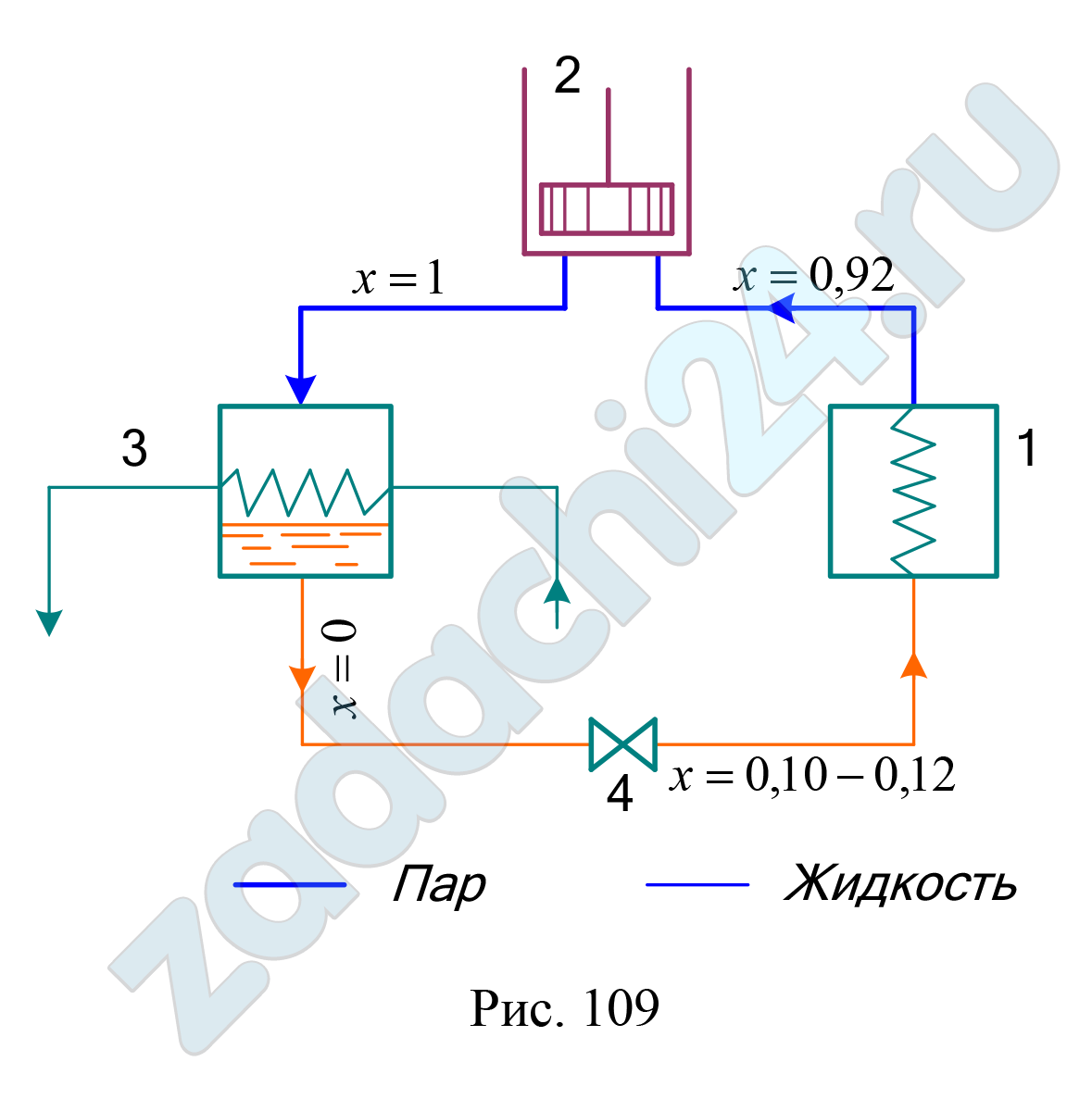

Ответ: εʹ = 8,32; εʹ/ε = 0,929.