Путеева Л.Е. Тухфатуллин Б.А. Сопротивление материалов ТГАСУ 2014
1.15 Ступенчатая колонна квадратного поперечного сечения (рис. 3.1, 3.2) выполнена из бетона с модулем упругости E = 2,0·104 МПа и загружена сосредоточенными силами F1, F2, F3. Требуется:
- Построить эпюру продольных сил.
- Определить площади поперечных сечений колонны, учитывая, что материал, из которого она изготовлена, неодинаково работает на растяжение и сжатие (расчетное сопротивление материала сжатию Rсж = 10 МПа; растяжению Rр = 1,2 МПа).
- Построить эпюру нормальных напряжений.
- Построить эпюру вертикальных перемещений сечений колонны.
Исходные данные для решения задачи определить согласно шифру по табл. 3.1.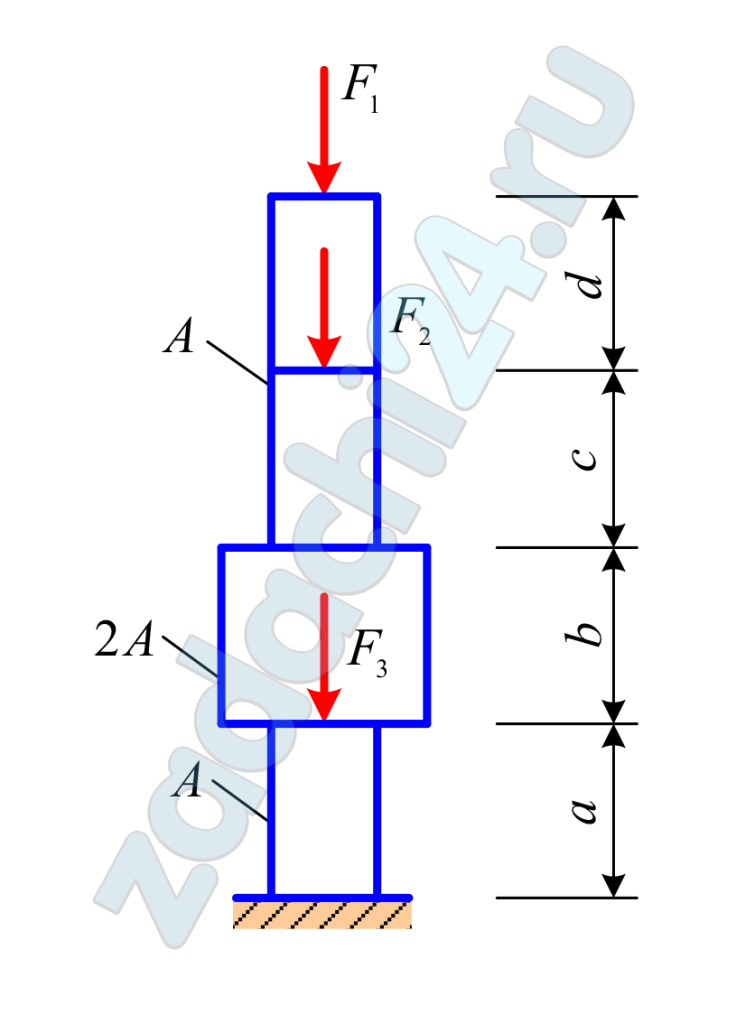
Таблица 3.1
| Вариант 213201 | |||||||
| Схема | а, м | b, м | с, м | d, м | F1, кН | F2, кН | F3, кН |
| 1 | 2,9 | 2,1 | 2,4 | 3,1 | 200 | 210 | -360 |
ВУЗ: ТГАСУ
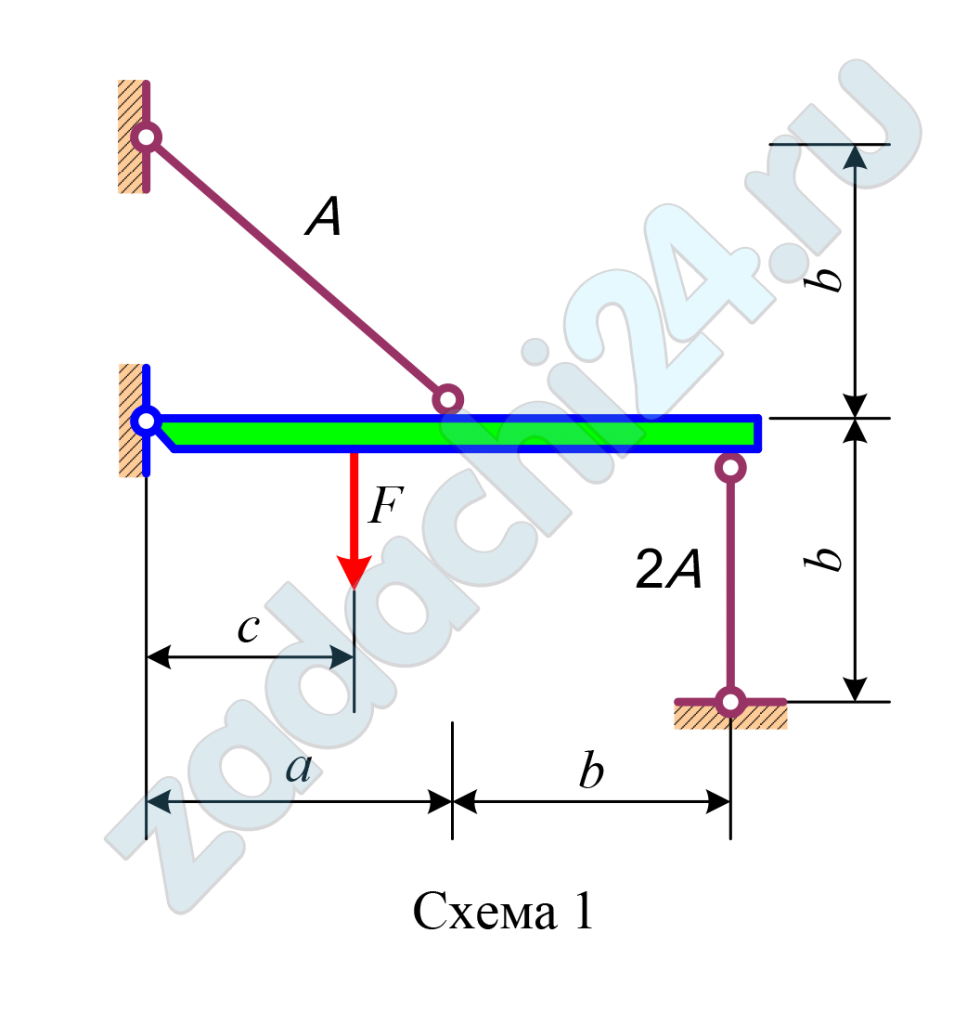
3.6 (Вариант 213201) Абсолютно жесткий брус опирается на шарнирно-неподвижную опору и прикреплен к двум стальным стержням (рис. 3.3, 3.4).
Требуется:
- Найти усилия и напряжения в стержнях, выразив их через силу F.
- Определить допускаемую нагрузку Fдоп, приравняв наибольшее из напряжений, возникающих в стержнях, расчетному сопротивлению R = 210 МПа .
- Определить предельную нагрузку Fпред, если предел текучести материала стержней σт = 240МПа.
Таблица 3.2
| Схема | А, см² | а, м | b, м | с, м |
| 1 | 12 | 2,1 | 2,1 | 1,3 |
ВУЗ: ТГАСУ
5.21 (Вариант 213201) К стальному валу круглого поперечного сечения приложены внешние скручивающие моменты М1, М2, М3, М4 (рис. 3.5, 3.6).
Требуется:
- Построить эпюру крутящих моментов.
- Определить из условия прочности диаметр вала (расчетное сопротивление материала на срез Rср).
- Построить эпюру углов закручивания поперечных сечений вала.
- Найти наибольший относительный угол закручивания и проверить жесткость вала, если задано допускаемое значение относительного угла закручивания [θ].
Модуль сдвига принять G = 0,8·105 МПа .
Таблица 3.3
| Схема | а, м | b, м | с, м | d, м |
| 1 | 1,3 | 2,0 | 1,2 | 2,0 |
Продолжение таблицы 3.3
| М1, кН·м | М2, кН·м | М3, кН·м | М4, кН·м | Rср, МПа | [θ], град/м |
| 28 | 26 | 15 | 13 | 80 | 1,0 |
ВУЗ: ТГАСУ
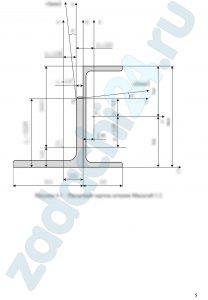
2.6 (Вариант 213201) Поперечное сечение элемента строительной конструкции состоит из двух прокатных профилей (рис. 3.7).
Требуется:
- Определить положение центра тяжести сечения.
- Вычислить осевые и центробежный моменты инерции относительно осей zС и yС, проходящих через центр тяжести сечения.
- Определить положение главных центральных осей инерции u и v.
- Найти значения главных центральных моментов инерции сечения.
- Вычертить поперечное сечение в масштабе и указать все размеры и все оси координат, в том числе и главные центральные оси.
Таблица 3.4
| Схема | Номер швеллера | Равнополочный уголок |
| 1 | 18 | 125×125×12 |
Примечание. Размеры равнополочного уголка приведены в мм.
Скачать файл (банки РФ) 200 RUBВУЗ: ТГАСУ
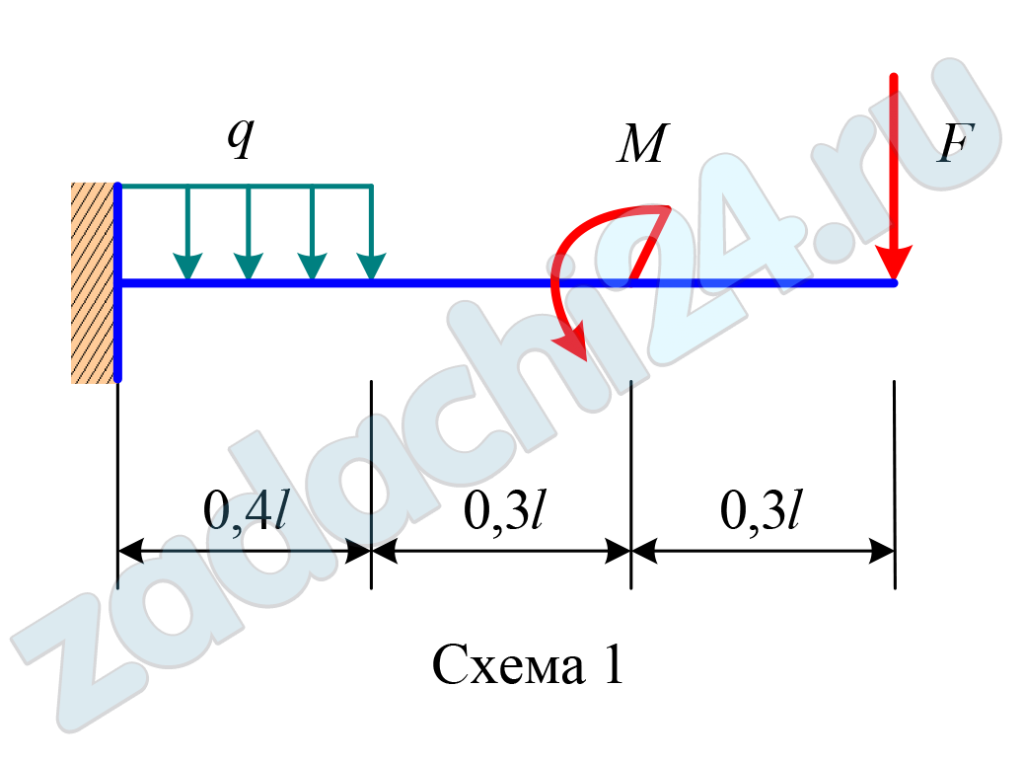
6.18 (Вариант 213201) Для балки-консоли (рис. 3.8) требуется:
- Определить опорные реакции.
- Записать в аналитическом виде выражения для внутренних усилий Qу и Мz на каждом участке балки.
- Построить эпюры внутренних усилий Qу и Мz.
- Определить размеры поперечного сечения при условии, что балка выполнена из дерева ( R = 8МПа ) и имеет круглое поперечное сечение.
Таблица 3.5
| Схема | l, м | F, кН | q, кН/м | М, кН·м |
| 1 | 2,0 | 1 | 12 | 11 |
ВУЗ: ТГАСУ
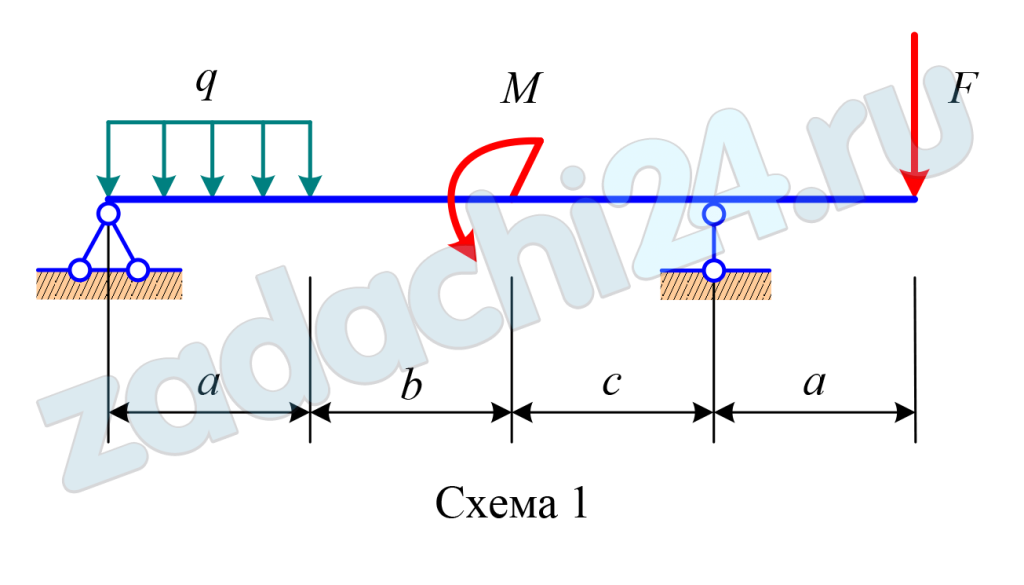
6.19 (Вариант 213201) Для шарнирно-опертой балки с консолью (рис. 3.9) требуется:
- Определить опорные реакции.
- Записать в аналитическом виде выражения для внутренних усилий Qу и Мz на каждом участке балки.
- Построить эпюры внутренних усилий Qу и Мz.
- Подобрать номер прокатного профиля двутавра из условия прочности при расчетном сопротивлении R = 210МПа.
Таблица 3.3
| Схема | а, м | b, м | с, м | F, кН | q, кН/м | М, кН·м |
| 1 | 1,2 | 2,6 | 2,6 | 1 | 12 | 11 |
ВУЗ: ТГАСУ
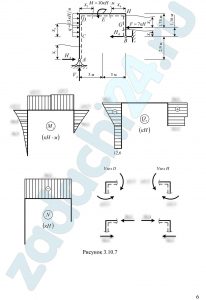
11.1 Статически определимая рама, расчетная схема которой показана на рис. 3.10, 3.11, загружена внешней нагрузкой.
Требуется:
- Определить опорные реакции.
- Записать выражения для внутренних усилий Mz, Qy и N на каждом из участков рамы.
- Построить эпюры внутренних усилий Mz, Qy и N.
- Выполнить проверку равновесия узлов рамы.
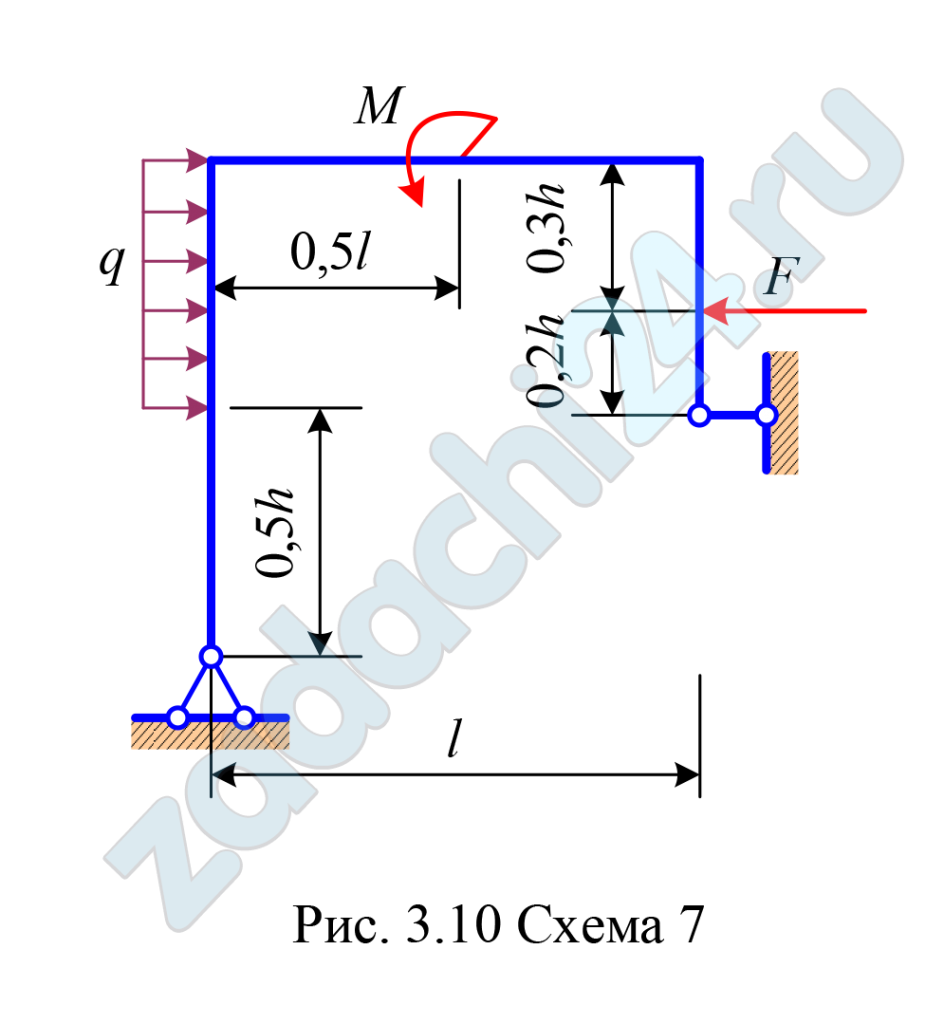
Данные взять из табл. 3.7.
Таблица 3.7
| Вариант 11207 | |||||
| Схема | l, м | h, м | F, кН | q, кН/м | М, кН·м |
| 7 | 6,0 | 5,8 | 7 | 13 | 10 |
ВУЗ: ТГАСУ
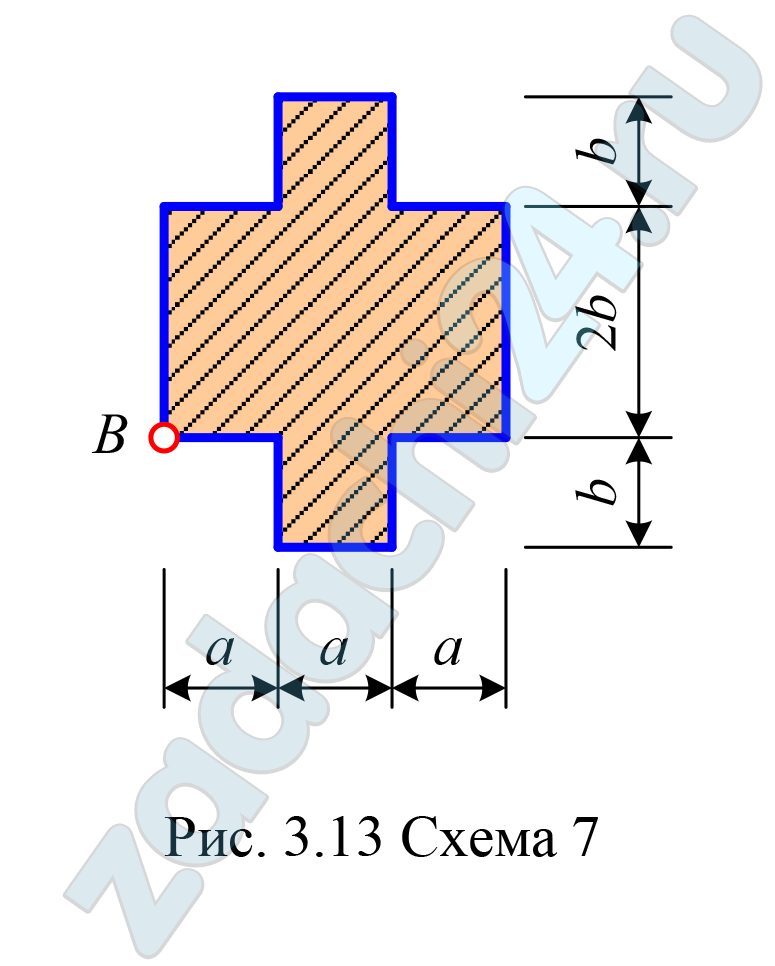
7.5 (Вариант 11207) Короткий стержень, поперечное сечение которого показано на рис. 3.12, 3.13, сжат продольной силой F, приложенной в точке B.
Требуется:
- Определить положение нейтральной линии.
- Определить в общем виде наибольшее растягивающее и наибольшее сжимающее напряжения, возникающие в поперечном сечении, выразив их через силу F.
- Найти величину допускаемой нагрузки Fдоп при заданных размерах поперечного сечения и расчетных сопротивлений материала на сжатие Rсж и растяжение Rр.
Таблица 3.8
| Схема | а, см | b, см | Rсж, МПа | Rр, МПа |
| 7 | 10 | 6 | 60 | 22 |
ВУЗ: ТГАСУ
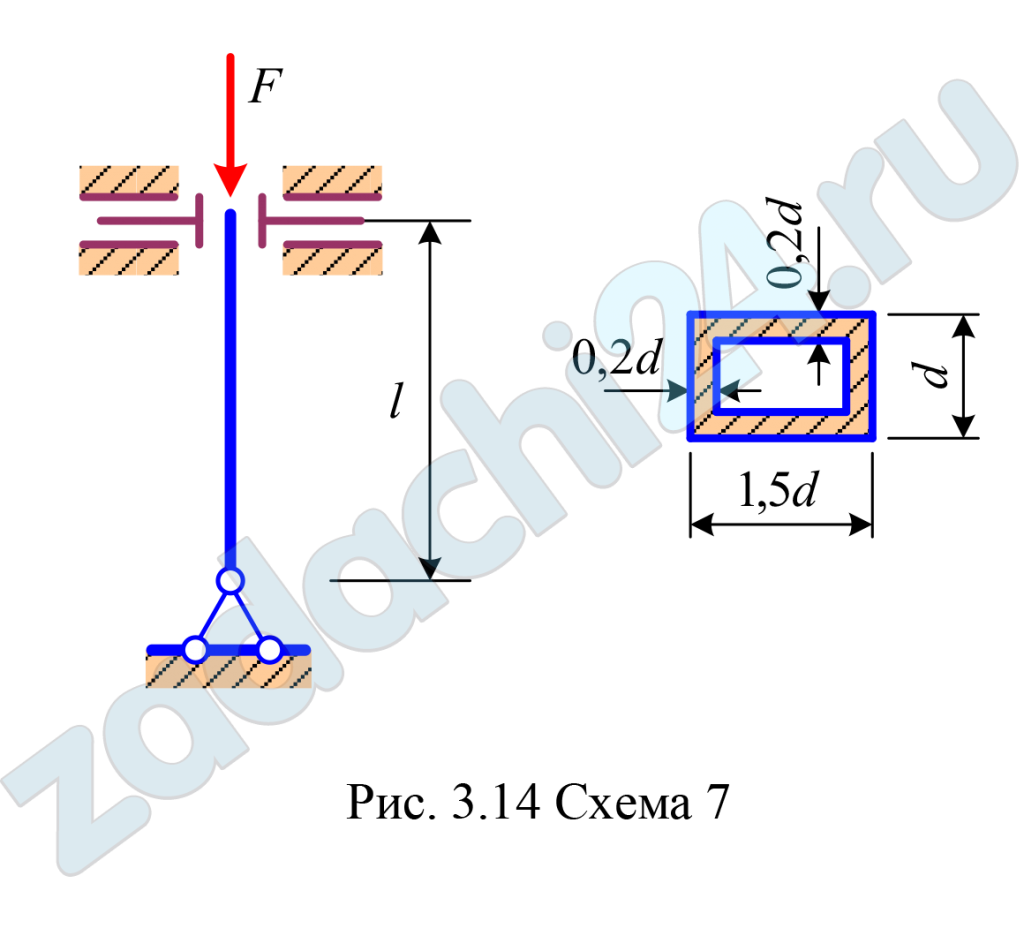
8.7 Стальной стержень длиной l загружен продольной силой F (рис. 3.14). Форма поперечного сечения стержня показана на рис. 3.15. При выполнении расчетов принять R = 210МПа, E = 2·105 МПа.
Требуется:
- Методом последовательных приближений определить размеры поперечного сечения стержня.
- Определить величину критической силы и коэффициент запаса по устойчивости.
Таблица 3.9
| F, кН | l, м | Схема колонны | Форма поперечного сечения |
| 200 | 5,0 | 5 | 7 |
ВУЗ: ТГАСУ
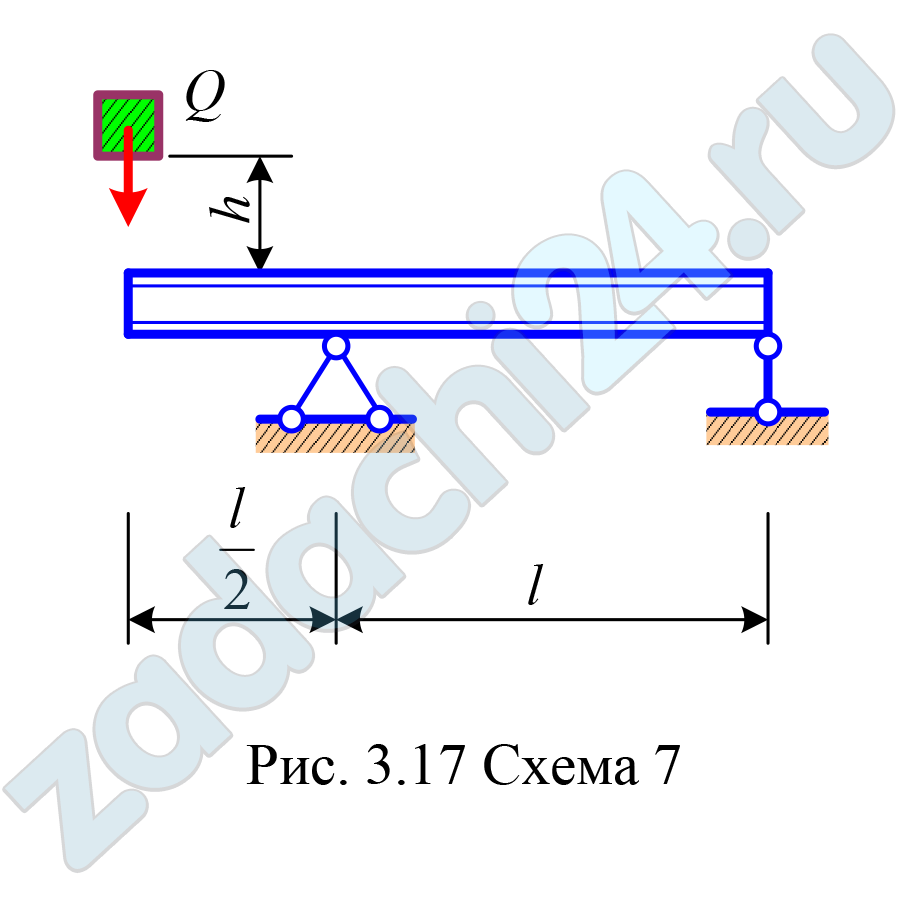
9.3 На стальную двутавровую балку (рис. 3.16, 3.17) с высоты h падает груз весом Q.
Требуется:
- Найти наибольшие нормальные напряжения, возникающие в балке в момент удара.
- Решить аналогичную задачу при условии, что правая опора заменена упругой с коэффициентом податливости α.
- Сравнить полученные результаты.
Модуль упругости Е = 2·105 МПа.
Таблица 3.10
| Схема | Номер двутавра | l, м | Q, кН | h, см | α, см/кН |
| 7 | 36 | 3,5 | 0,8 | 5 | 0,75 |
ВУЗ: ТГАСУ











![Путеева Л.Е. Тухфатуллин Б.А. Сопротивление материалов ТГАСУ 2014 Задача 5 К стальному валу круглого поперечного сечения приложены внешние скручивающие моменты М1, М2, М3, М4 (рис. 3.5, 3.6). Требуется: Построить эпюру крутящих моментов. Определить из условия прочности диаметр вала (расчетное сопротивление материала на срез Rср). Построить эпюру углов закручивания поперечных сечений вала. Найти наибольший относительный угол закручивания и проверить жесткость вала, если задано допускаемое значение относительного угла закручивания [θ]. Модуль сдвига принять G = 0,8·105 МПа . Данные взять из табл. 3.3.](https://zadachi24.ru/wp-content/uploads/2023/10/sopromat_5.21.0-1024x592.png)
![К стальному валу круглого поперечного сечения приложены внешние скручивающие моменты М1, М2, М3, М4 (рис. 3.5, 3.6). Требуется: Построить эпюру крутящих моментов. Определить из условия прочности диаметр вала (расчетное сопротивление материала на срез Rср). Построить эпюру углов закручивания поперечных сечений вала. Найти наибольший относительный угол закручивания и проверить жесткость вала, если задано допускаемое значение относительного угла закручивания [θ]](https://zadachi24.ru/wp-content/uploads/2023/10/sopromat_5.21.0_page_1-205x300.jpg)
![К стальному валу круглого поперечного сечения приложены внешние скручивающие моменты М1, М2, М3, М4 (рис. 3.5, 3.6). Требуется: Построить эпюру крутящих моментов. Определить из условия прочности диаметр вала (расчетное сопротивление материала на срез Rср). Построить эпюру углов закручивания поперечных сечений вала. Найти наибольший относительный угол закручивания и проверить жесткость вала, если задано допускаемое значение относительного угла закручивания [θ]](https://zadachi24.ru/wp-content/uploads/2023/10/sopromat_5.21.0_page_2-205x300.jpg)
![К стальному валу круглого поперечного сечения приложены внешние скручивающие моменты М1, М2, М3, М4 (рис. 3.5, 3.6). Требуется: Построить эпюру крутящих моментов. Определить из условия прочности диаметр вала (расчетное сопротивление материала на срез Rср). Построить эпюру углов закручивания поперечных сечений вала. Найти наибольший относительный угол закручивания и проверить жесткость вала, если задано допускаемое значение относительного угла закручивания [θ]](https://zadachi24.ru/wp-content/uploads/2023/10/sopromat_5.21.0_page_3-205x300.jpg)
![К стальному валу круглого поперечного сечения приложены внешние скручивающие моменты М1, М2, М3, М4 (рис. 3.5, 3.6). Требуется: Построить эпюру крутящих моментов. Определить из условия прочности диаметр вала (расчетное сопротивление материала на срез Rср). Построить эпюру углов закручивания поперечных сечений вала. Найти наибольший относительный угол закручивания и проверить жесткость вала, если задано допускаемое значение относительного угла закручивания [θ]](https://zadachi24.ru/wp-content/uploads/2023/10/sopromat_5.21.0_page_4-205x300.jpg)
![К стальному валу круглого поперечного сечения приложены внешние скручивающие моменты М1, М2, М3, М4 (рис. 3.5, 3.6). Требуется: Построить эпюру крутящих моментов. Определить из условия прочности диаметр вала (расчетное сопротивление материала на срез Rср). Построить эпюру углов закручивания поперечных сечений вала. Найти наибольший относительный угол закручивания и проверить жесткость вала, если задано допускаемое значение относительного угла закручивания [θ]](https://zadachi24.ru/wp-content/uploads/2023/10/sopromat_5.21.0_page_5-206x300.jpg)