Лехов О.С. и др. Теоретическая и прикладная механика Екатеринбург РГППУ 2012
2.62.0 Тема «Плоская система сил»
На схемах (рис. 1) показаны три способа закрепления бруса, ось которого – ломаная линия. Задаваемая нагрузка (см. табл. 1) и размеры (м) во всех трех случаях одинаковы. Определить реакции опор для того способа закрепления бруса, при котором реакция, указанная в табл. 1, имеет наименьший модуль.
Таблица 1 – Исходные данные
| Вариант | Р, кН | М, кН·м | q, кН/м | Расстояния, м | ||
| a | b | c | ||||
| 531 | 20 | 12 | 4 | 2 | 2 | 4 |
Продолжение таблицы 1
| Номер схемы (рис. 1) | α, град | Исследуемая реакция |
| 1 | 60 | YA |
ВУЗ: РГППУ
4.8 (Вариант 531) Тема «Пространственная система сил»
На горизонтальный вал насажены колесо 1 радиусом r1=20 см, колесо 2 радиусом r2=30 см и прикреплен перпендикулярно оси вала (параллельно оси х) рычаг СD длиной l=20 см. К одному колесу приложена сила F, образующая с горизонталью угол α1, а к другому – сила Т2, образующая с вертикалью угол α2; к рычагу приложена вертикальная сила Р (рис. 4, схемы 4 – 7). Пренебрегая весом вала, колес и рычага, определить силу Р, при которой вал находится в равновесии, а также реакции подшипников А и В.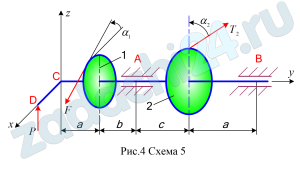
Таблица 3
| Номер условия |
Номер схемы (рис. 4) |
Расстояния, м | Силы, Н | Углы, град | ||||
| a | b | c | F | T2 | α1 | α2 | ||
| 2 | 5 | 1,4 | 1,5 | 1,4 | 1000 | 300 | 0 | 60 |
ВУЗ: РГППУ
7.8 (Вариант 531) Тема «Плоское движение твердого тела»
Кривошип ОА длиной R вращается вокруг неподвижной оси О с постоянной угловой скоростью ω и приводит в движение шатун АВ длиной l и ползун В. Для заданного положения механизма найти скорости и ускорения ползуна В и точки С, а также угловую скорость и угловое ускорение звена, которому эта точка принадлежит.
Схемы механизмов приведены на рис. 9, а необходимые для расчета данные – в табл. 7.
Таблица 7
| R, см | l, см | α, град | β, град | ω, c-1 | Номер схемы (рис. 9) | АС |
| 40 | 50 | 60 | 45 | 10 | 1 | 0,2 |
Примечание. Если при заданных значениях углов окажется, что шатун АВ перпендикулярен направляющим ползуна (см. рис. 9, схемы 1, 6), то значение угла β следует принять равным 15º.
Скачать файл (оплата в RUB)
ВУЗ: РГППУ
1.9 Тема «Растяжение – сжатие»
Произвести расчет стержня постоянного сечения (рис. 1) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σ]=210 МПа и модулем Юнга Е=2,1·105 МПа. Требуется:
1) вычислить продольные силы на участках стержня и построить эпюру продольных сил N по его длине;
2) определить размеры поперечного сечения (сторону квадрата или диаметр);
3) вычислить нормальные напряжения на участках стержня и построить эпюру нормальных напряжений σ по его длине;
4) вычислить деформации участков стержня и построить эпюру перемещений δ.
Исходные цифровые данные приведены в табл. 1. ![Тема «Растяжение – сжатие» Произвести расчет стержня постоянного сечения (рис. 1) на прочность и жесткость. Материал стержня – сталь с допускаемым напряжением [σ]=210 МПа и модулем Юнга Е=2,1·105 МПа. Требуется: 1) вычислить продольные силы на участках стержня и построить эпюру продольных сил N по его длине; 2) определить размеры поперечного сечения (сторону квадрата или диаметр); 3) вычислить нормальные напряжения на участках стержня и построить эпюру нормальных напряжений σ по его длине; 4) вычислить деформации участков стержня и построить эпюру перемещений δ. Исходные цифровые данные приведены в табл. 1.](https://zadachi24.ru/wp-content/uploads/2019/05/sopromat_1.9.0.png "Лехов О.С. и др. Теоретическая и прикладная механика Екатеринбург РГППУ 2012 Задача 4")
Таблица 1
| Вариант 531 | |||
| l1, м | l2, м | l3, м | l4, м |
| 0,9 | 0,8 | 1,5 | 0,9 |
Продолжение таблицы 1
| F1, МН | F2, МН | F3, МН | Номер схемы (рис. 1) |
Форма сечения |
| 1,4 | 0,4 | 1,7 | 1 | Квадрат |
ВУЗ: РГППУ
5.14 Тема «Кручение»
К стальному ступенчатому валу, имеющему сплошное цилиндрическое поперечное сечение, приложены четыре крутящих момента (рис. 3). Левый конец вала жестко закреплен в опоре, а правый – свободен. Требуется:
1) построить эпюру крутящих моментов Tк по длине вала;
2) при заданном значении допускаемого напряжения на кручение [τк] определить диаметры d1 и d2 вала из расчета на прочность (полученные результаты округлить).
Исходные цифровые данные приведены в табл. 2.![Тема «Кручение» К стальному ступенчатому валу, имеющему сплошное цилиндрическое поперечное сечение, приложены четыре крутящих момента (рис. 3). Левый конец вала жестко закреплен в опоре, а правый – свободен. Требуется: 1) построить эпюру крутящих моментов Tк по длине вала; 2) при заданном значении допускаемого напряжения на кручение [τк] определить диаметры d1 и d2 вала из расчета на прочность (полученные результаты округлить). Исходные цифровые данные приведены в табл. 2.](https://zadachi24.ru/wp-content/uploads/2019/05/sopromat_5.14.0.png "Лехов О.С. и др. Теоретическая и прикладная механика Екатеринбург РГППУ 2012 Задача 5")
Таблица 2
| Вариант 531 | ||||||||
| Крутящие моменты, кН·м | Расстояния, м | [τк], МПа | Номер схемы (рис. 3) |
|||||
| Т1 | Т2 | Т3 | Т4 | a | b | c | ||
| 5,5 | 2,5 | 1,5 | 0,5 | 1,2 | 1,2 | 1,2 | 35 | 1 |
![Тема «Кручение» К стальному ступенчатому валу, имеющему сплошное цилиндрическое поперечное сечение, приложены четыре крутящих момента (рис. 3). Левый конец вала жестко закреплен в опоре, а правый – свободен. Требуется: 1) построить эпюру крутящих моментов Tк по длине вала; 2) при заданном значении допускаемого напряжения на кручение [τк] определить диаметры d1 и d2 вала из расчета на прочность (полученные результаты округлить).](https://zadachi24.ru/wp-content/uploads/2018/08/sopromat_5.14.0_page_1.jpg)
![Тема «Кручение» К стальному ступенчатому валу, имеющему сплошное цилиндрическое поперечное сечение, приложены четыре крутящих момента (рис. 3). Левый конец вала жестко закреплен в опоре, а правый – свободен. Требуется: 1) построить эпюру крутящих моментов Tк по длине вала; 2) при заданном значении допускаемого напряжения на кручение [τк] определить диаметры d1 и d2 вала из расчета на прочность (полученные результаты округлить).](https://zadachi24.ru/wp-content/uploads/2018/08/sopromat_5.14.0_page_2.jpg)
![Тема «Кручение» К стальному ступенчатому валу, имеющему сплошное цилиндрическое поперечное сечение, приложены четыре крутящих момента (рис. 3). Левый конец вала жестко закреплен в опоре, а правый – свободен. Требуется: 1) построить эпюру крутящих моментов Tк по длине вала; 2) при заданном значении допускаемого напряжения на кручение [τк] определить диаметры d1 и d2 вала из расчета на прочность (полученные результаты округлить).](https://zadachi24.ru/wp-content/uploads/2018/08/sopromat_5.14.0_page_3.jpg)
![Тема «Кручение» К стальному ступенчатому валу, имеющему сплошное цилиндрическое поперечное сечение, приложены четыре крутящих момента (рис. 3). Левый конец вала жестко закреплен в опоре, а правый – свободен. Требуется: 1) построить эпюру крутящих моментов Tк по длине вала; 2) при заданном значении допускаемого напряжения на кручение [τк] определить диаметры d1 и d2 вала из расчета на прочность (полученные результаты округлить).](https://zadachi24.ru/wp-content/uploads/2018/08/sopromat_5.14.0_page_4.jpg)
ВУЗ: РГППУ
6.11 (Вариант 531) Тема «Поперечный изгиб»
Для заданной схемы балки (рис. 5) требуется:
1) записать уравнение в общем виде для определения поперечных сил Q и изгибающих моментов Ми на каждом участке балки;
2) построить эпюры поперечных сил Q и изгибающего момента Mи;
3) найти максимальный изгибающий момент Мmax и подобрать по ГОСТу стальную балку двутаврового поперечного сечения. Допускаемое напряжение на изгиб принять равным [σи]=150 МПа.
Исходные цифровые данные представлены в табл. 3.![Тема «Поперечный изгиб» Для заданной схемы балки (рис. 5) требуется: 1) записать уравнение в общем виде для определения поперечных сил Q и изгибающих моментов Ми на каждом участке балки; 2) построить эпюры поперечных сил Q и изгибающего момента Mи; 3) найти максимальный изгибающий момент Мmax и подобрать по ГОСТу стальную балку двутаврового поперечного сечения. Допускаемое напряжение на изгиб принять равным [σи]=150 МПа.](https://zadachi24.ru/wp-content/uploads/2019/05/sopromat_6.11.0.png "Лехов О.С. и др. Теоретическая и прикладная механика Екатеринбург РГППУ 2012 Задача 6")
Таблица 3
| а, м | b, м | с, м | l, м |
| 2,8 | 4,0 | 2,2 | 12 |
Продолжение таблицы 3
| М, кН·м | F, кН | q, кН/м | Номер схемы (рис. 5) |
| 8 | 18 | 20 | 1 |
ВУЗ: РГППУ
6.12 (Вариант 531) Тема «Поперечный изгиб»
Произвести расчет на прочность консольной балки (рис. 9). Материал балки – сталь с допускаемым напряжением при изгибе [σи]=200 МПа.
Требуется:
1) построить эпюры поперечных сил и изгибающих моментов;
2) определить размеры поперечного сечения балки: для круглого сечения — диаметр; для прямоугольного – значения сторон, считая, что отношение высоты сечения к его ширине равно двум.
Исходные цифровые данные представлены в табл. 4.![Тема «Поперечный изгиб» Произвести расчет на прочность консольной балки (рис. 9). Материал балки – сталь с допускаемым напряжением при изгибе [σи]=200 МПа. Требуется: 1) построить эпюры поперечных сил и изгибающих моментов; 2) определить размеры поперечного сечения балки: для круглого сечения - диаметр; для прямоугольного – значения сторон, считая, что отношение высоты сечения к его ширине равно двум.](https://zadachi24.ru/wp-content/uploads/2019/05/sopromat_6.12.0.png "Лехов О.С. и др. Теоретическая и прикладная механика Екатеринбург РГППУ 2012 Задача 7")
Таблица 4
| F, кН | М, кН·м | q, кН/м | а, м | b, м | Номер схемы (рис. 9) |
| 5 | 3 | 5,3 | 1,2 | 1,2 | 1 |
ВУЗ: РГППУ
