Лапшин В.Л. Сопротивление материалов ИРНИТУ 2020
1.14 Расчет ступенчатого стержня на прочность при центральном растяжении и сжатии
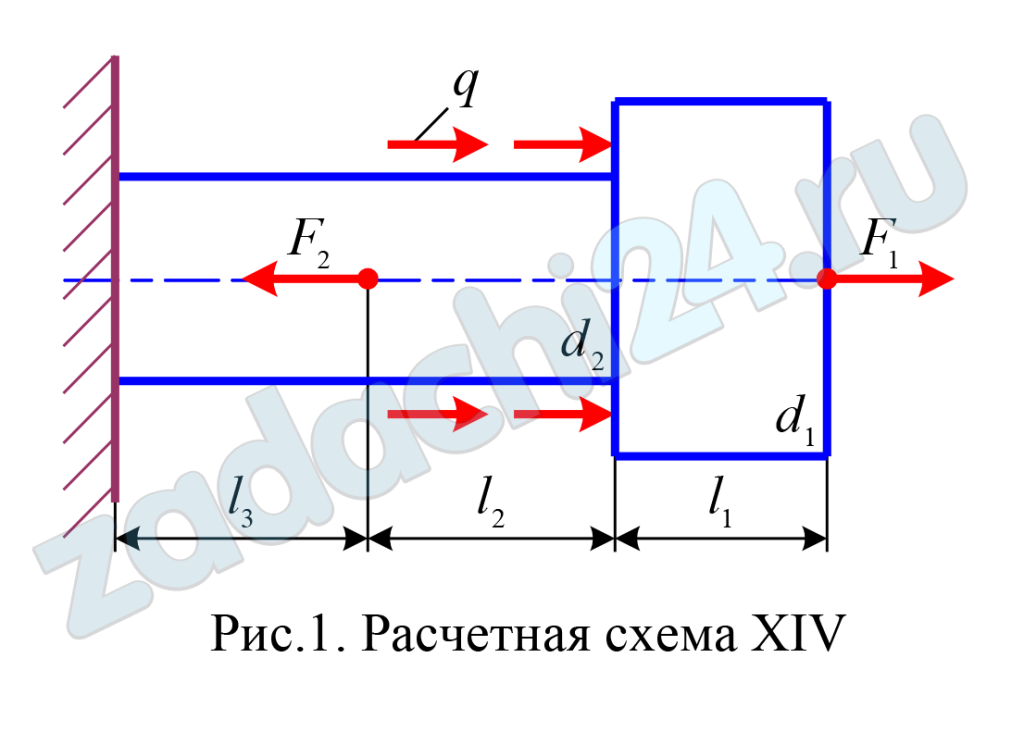
Для заданного ступенчатого стержня (табл. 3) требуется:
а) построить эпюру продольных сил N;
б) рассчитать диаметры d1, d2 ступенчатого стержня;
в) построить эпюру нормальных напряжений σ.
Исходные данные взять из табл.2.
Таблица 2 – Исходные данные для задачи 1
| Вариант 186 | |||||||
| F1, кН | F2, кН | q, кН/м | l1, м | l2, м | l3, м | [σ]Р, МПа | [σ]С, МПа |
| 24 | 35 | 46 | 1 | 1,1 | 1,7 | 100 | 330 |
ВУЗ: ИРНИТУ
2.5 Определение геометрических характеристик составного симметричного сечения из стандартных профилей
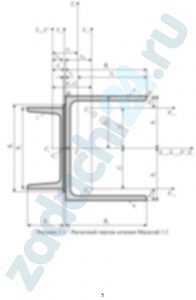
Для симметричного сечения из стандартных профилей (табл. 5) требуется:
а) определить положение центра тяжести сечения;
б) определить главные центральные моменты инерции IXc, IYc;
в) определить момент сопротивления WXc относительно оси изгиба Х.
Исходные данные взять из табл. 4. Размеры стандартных профилей (двутавр, швеллер, не равнополочный уголок) взять из таблиц сортамента.
Таблица 4 – Исходные данные для задачи 2
| Вариант | Швеллер | Не равнополочный уголок | Полоса, мм |
| 186 | 14а | 140×90×8 | 150×4 |
ВУЗ: ИРНИТУ
5.20 Расчет круглого ступенчатого вала на прочность и жесткость при кручении
Ступенчатый вал защемлен одним концом и загружен внешними скручивающими моментами М1, М2, М3 (табл. 7). Материал вала – сталь 3, модуль сдвига G = 0,8·105 МПа.
Требуется:
а) построить эпюру крутящих моментов;
б) определить из условий прочности и жесткости диаметры вала d1, d2;
в) построить эпюру абсолютных углов закручивания сечений по отношению к неподвижному сечению в заделке.
Исходные данные взять из табл.6.
Таблица 6 – Исходные данные для задачи 3
| Вариант | М1, кН·м | М2, кН·м | М3, кН·м |
| 186 | 1,4 | 3,5 | 0,8 |
Продолжение таблицы 6
| l1, м | l2, м | l3, м | l4, м | [τ], МПа | [θо], град/м |
| 1,8 | 1,8 | 1 | 1,2 | 70 | 0,5 |
ВУЗ: ИРНИТУ
6.16 Расчет статически определимой консольной балки на прочность и жесткость
Для заданной консольной балки требуется (табл. 9):
а) построить эпюры внутренних силовых факторов Q и М в балке;
б) проверить на прочность по нормальным напряжениям сечение из задачи 2;
в) рассчитать угол поворота и прогиб в точке К методом начальных параметров.
Исходные данные принять по табл.8.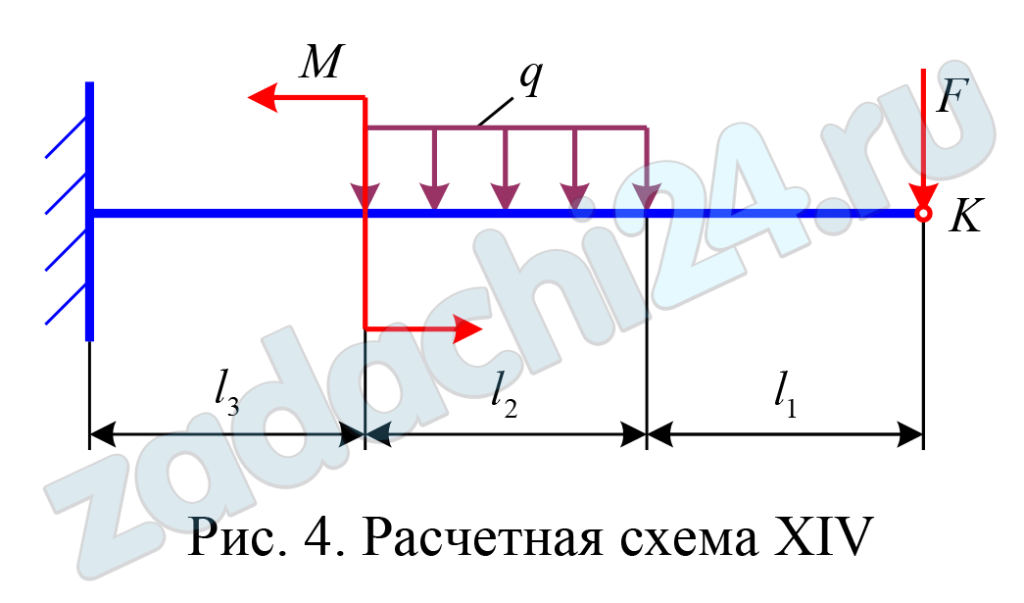
Таблица 8 – Исходные данные для задачи 4
| Вариант 186 | |||||||
| F, кН | q, кН/м | М, кН·м | l1, м | l2, м | l3, м | [σ], МПа | [τ], МПа |
| 22 | 25 | 25 | 1,8 | 0,9 | 1,5 | 110 | 70 |
ВУЗ: ИРНИТУ
6.17 Расчет статически определимой шарнирно закрепленной балки на прочность
Для двух опорной балки (табл. 11) требуется:
а) построить эпюры внутренних силовых факторов Q и М в балке;
б) подобрать размеры поперечных сечений разной формы (круг, прямоугольник, швеллер, двутавр) из условия прочности по нормальным напряжениям;
в) произвести полную проверку на прочность двутаврового сечения.
Исходные данные взять из табл.10.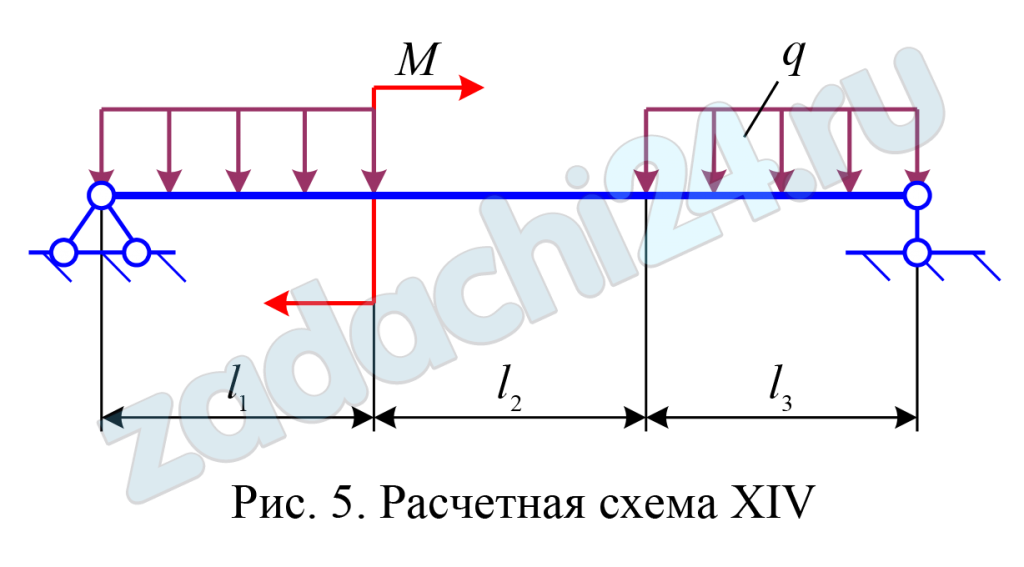
Таблица 10 – Исходные данные для задачи 5
| Вариант 186 | ||||||
| q, кН/м | М, кН·м | l1, м | l2, м | l3, м | [σ], МПа | [τ], МПа |
| 40 | 60 | 1,5 | 1,2 | 1,1 | 190 | 115 |
ВУЗ: ИРНИТУ
8.4 Проектный расчет центрально сжатого стержня на устойчивость
Стержень длиной l заданного сечения (табл. 13) с заданным способом закрепления (рис.1) сжимается нагрузкой. Требуется:
а) из расчета на устойчивость с помощью таблиц коэффициентов снижения допускаемых напряжений определить размеры сечения стержня;
б) определить величину критической силы;
в) определить фактический коэффициент запаса устойчивости.
Исходные данные взять из табл.12. Модуль упругости принять равным: сталь − ЕСТ = 2·105 МПа; дюралюминий − ЕД = 0,7·105 МПа.
Если при расчете гибкости λ на первом приближении значение гибкости получается больше 220 (λ = (μ·l)/iMIN > 220), необходимо уменьшить длину l (в 2, 3, 4 раза), чтобы λ ≤ 220 и далее в расчете использовать уменьшенную длину.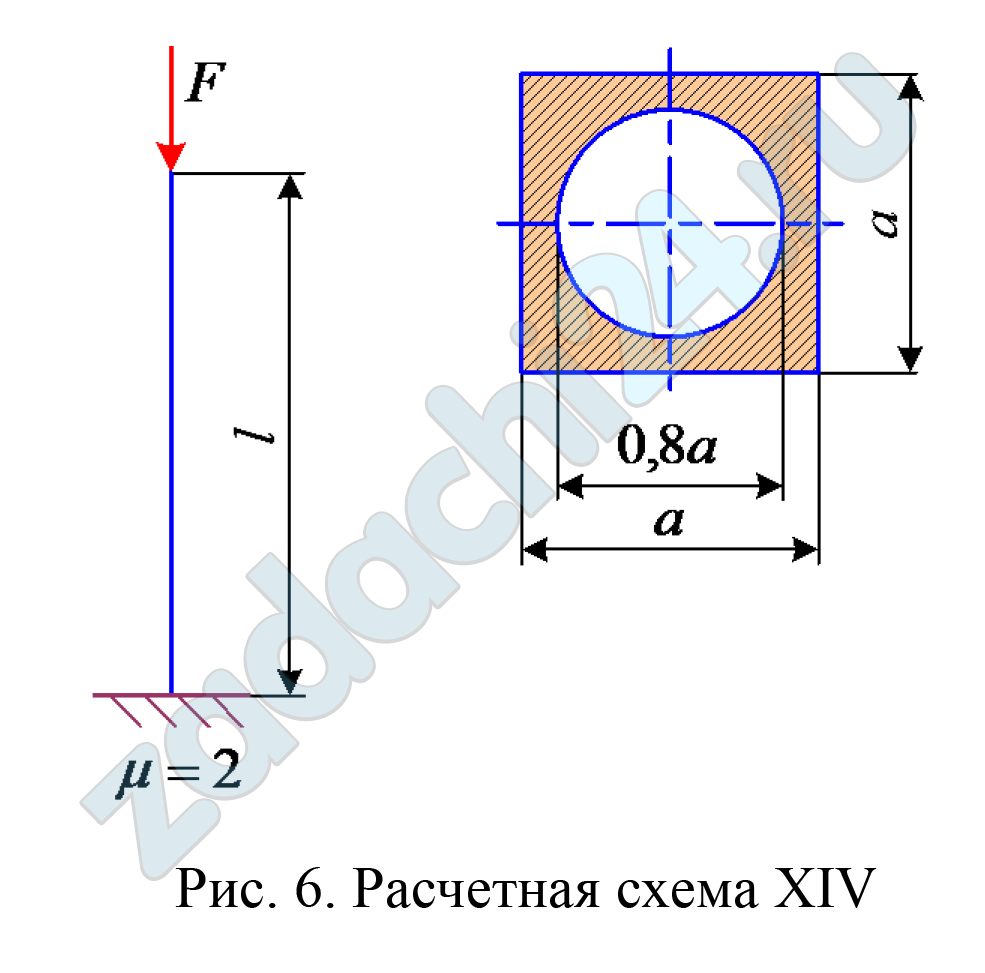
Таблица 12 – Исходные данные для задачи 6
| Вариант 186 | ||||||
| Способ
закрепления (рис. 1) |
Материал
стержня |
σТ, МПа | σПЦ, МПа | F, кН | l, м | nПР |
| I | Сталь 45 | 360 | 305 | 310 | 4,2 | 1,4 |
ВУЗ: ИРНИТУ