Гребенюк Г.И. Сопротивление материалов Сибстрин 2015
1.12 Статически определимая система
Дано: Стойка из бетона жёстко закреплена на нижнем конце и нагружена силами F1, F2 и q, действующими вдоль оси стержня.
Е = 0,27·105 МПа, Rc = 12 МПа, Rt = 0,9 МПа.
Требуется:
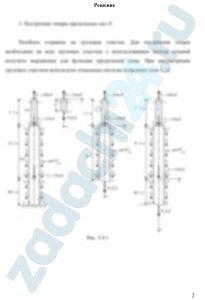
- Построить эпюру продольных сил N.
- Определить требуемые площади поперечных сечений А из условий прочности и соблюдения при этом заданного соотношения площадей на различных участках.
- Построить эпюру нормальных напряжений σ.
- Построить эпюру перемещений сечений u.
- Выполнить проверку жёсткости. [Δl] = (0,01 ÷ 0,02)l, [u] = 0,001l. Здесь l – длина стержня.
![Гребенюк Г.И. Сопротивление материалов Сибстрин 2015 Задача 1.1 Статически определимая система Дано: Стойка из бетона жёстко закреплена на нижнем конце и нагружена силами F1, F2 и q, действующими вдоль оси стержня. Е = 0,27·105 МПа, Rc = 12 МПа, Rt = 0,9 МПа. Требуется: Построить эпюру продольных сил N. Определить требуемые площади поперечных сечений А из условий прочности и соблюдения при этом заданного соотношения площадей на различных участках. Построить эпюру нормальных напряжений σ. Построить эпюру перемещений сечений u. Выполнить проверку жёсткости. [Δl] = (0,01 ÷ 0,02)l, [u] = 0,001l. Здесь l – длина стержня.](https://zadachi24.ru/wp-content/uploads/2023/04/sopromat_1.12.0-264x300.png)
Таблица 1.1
| Вариант | а, м | F1, кН | F2, кН | F3, кН | q, кН/м |
| 9 | 1 | 100 | 110 | 150 | 60 |
ВУЗ: Сибстрин
10.1 Плоское напряженное состояние
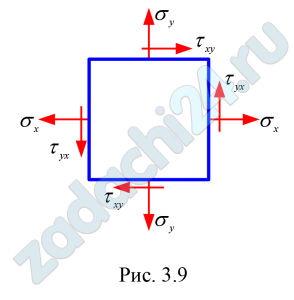
ДАНО: на площадках рассматриваемого элемента объёма заданы напряжения (рис. 3.9). Варианты остальных исходных данных приведены в таблице 3.5.
ТРЕБУЕТСЯ: 1. Выполнить чертеж с учетом знака напряжений.
- Определить главные напряжения и положение главных площадок.
- Найти экстремальные касательные напряжения и положение соответствующих им площадок.
- Найти деформации в направлении заданных осей x, y и главные деформации.
- Проверить выполнение условий прочности по различным теориям прочности: 1) теория максимальных нормальных напряжений; 2) теория наибольших линейных деформаций; 3) теория максимальных касательных напряжений; 4) энергетическая теория; 5) теория прочности Кулона-Мора.
Таблица 2.1
| № вар. (К) | σх, МПа | σу, МПа | τху, МПа | материал |
| 9 | -40 | 40 | 50 | алюминий |
ВУЗ: Сибстрин
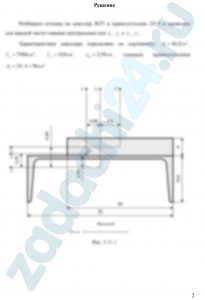
2.3 Определение геометрических характеристик плоских сечений
Дано поперечное сечение стержня (рис. 3.11).
Требуется:
- Начертить заданное поперечное сечение в масштабе, проставить размеры в сантиметрах.
- Определить координаты центра тяжести сечения и провести горизонтальную и вертикальную центральные оси.
- Определить осевые и центробежный моменты инерции сечения относительно проведенных центральных осей.
- Определить положение главных центральных осей инерции и показать их на чертеже.
- Вычислить величины главных центральных моментов инерции.
- Определить величины главных центральных радиусов инерции сечения.

Таблица 2.3
| Вариант | Прямоугольник | Номер
швеллера |
| 9 | 24×4 | 33 |
ВУЗ: Сибстрин
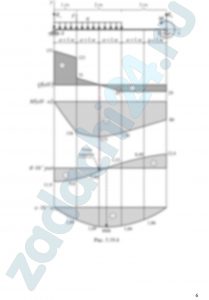
6.14 Для балок, расчетные схемы которых показаны на рис. 3.19 и приведены данные нагрузок и размеров в табл.4.1, требуется:
- Определить реакции опор. Построить эпюры поперечных сил Qy и изгибающих моментов Mz. Определить положение опасных сечений.
- Из условия прочности по нормальным напряжениям определить размеры поперечного сечения балки в двух вариантах: «а» и «б» (рис. 3.18). Принять R = 200 МПа.
- Выполнить проверку прочности по касательным напряжениям. Принять Rs = 120 МПа.
- Для варианта «б» поперечного сечения сделать проверку прочности материала в точке, в которой имеет место неблагоприятное сочетание нормальных σх и касательных τух напряжений. Применить гипотезы прочности – наибольших касательных напряжений и энергетическую.
- Для варианта «б» поперечного сечения определить его размеры из расчета по предельной несущей способности. Принять σs = 240 МПа; k = 1,2.
- Для заданной балки записать уравнения прогибов и углов поворота по методу начальных параметров. Определить начальные параметры (сечение вариант «а»).
- Вычислить значение прогиба на расстоянии 3а (2а), и угла поворота на расстоянии 5а от начала координат.
- Проверить выполнение условия жесткости балки, приняв [υ] = 1/400l, где l – пролет балки (расстояние между опорами, или длина консольной части).
![Гребенюк Г.И. Сопротивление материалов Сибстрин 2015 Задача 4.1 Для балок, расчетные схемы которых показаны на рис. 3.19 и приведены данные нагрузок и размеров в табл.4.1, требуется: Определить реакции опор. Построить эпюры поперечных сил Qy и изгибающих моментов Mz. Определить положение опасных сечений. Из условия прочности по нормальным напряжениям определить размеры поперечного сечения балки в двух вариантах: "а" и "б" (рис. 3.18). Принять R = 200 МПа. Выполнить проверку прочности по касательным напряжениям. Принять Rs = 120 МПа. Для варианта "б" поперечного сечения сделать проверку прочности материала в точке, в которой имеет место неблагоприятное сочетание нормальных σх и касательных τух напряжений. Применить гипотезы прочности – наибольших касательных напряжений и энергетическую. Для варианта "б" поперечного сечения определить его размеры из расчета по предельной несущей способности. Принять σs = 240 МПа; k = 1,2. Для заданной балки записать уравнения прогибов и углов поворота по методу начальных параметров. Определить начальные параметры (сечение вариант «а»). Вычислить значение прогиба на расстоянии 3а (2а), и угла поворота на расстоянии 5а от начала координат. Проверить выполнение условия жесткости балки, приняв [υ] = 1/400l, где l – пролет балки (расстояние между опорами, или длина консольной части).](https://zadachi24.ru/wp-content/uploads/2023/04/sopromat_6.14.0.b-1024x551.png)
Таблица 4.1
| Вариант | q (кН/м) | F (кН) | М (кН·м) | а (м) |
| 9 | 30 | 90 | 80 | 1 |
ВУЗ: Сибстрин
















![Гребенюк Г.И. Сопротивление материалов Сибстрин 2015 Задача 4.1 Для балок, расчетные схемы которых показаны на рис. 3.19 и приведены данные нагрузок и размеров в табл.4.1, требуется: Определить реакции опор. Построить эпюры поперечных сил Qy и изгибающих моментов Mz. Определить положение опасных сечений. Из условия прочности по нормальным напряжениям определить размеры поперечного сечения балки в двух вариантах: "а" и "б" (рис. 3.18). Принять R = 200 МПа. Выполнить проверку прочности по касательным напряжениям. Принять Rs = 120 МПа. Для варианта "б" поперечного сечения сделать проверку прочности материала в точке, в которой имеет место неблагоприятное сочетание нормальных σх и касательных τух напряжений. Применить гипотезы прочности – наибольших касательных напряжений и энергетическую. Для варианта "б" поперечного сечения определить его размеры из расчета по предельной несущей способности. Принять σs = 240 МПа; k = 1,2. Для заданной балки записать уравнения прогибов и углов поворота по методу начальных параметров. Определить начальные параметры (сечение вариант «а»). Вычислить значение прогиба на расстоянии 3а (2а), и угла поворота на расстоянии 5а от начала координат. Проверить выполнение условия жесткости балки, приняв [υ] = 1/400l, где l – пролет балки (расстояние между опорами, или длина консольной части).](https://zadachi24.ru/wp-content/uploads/2023/04/sopromat_6.14.0.а-1024x542.png)