Горюнов С.В. Семенов В.А. РГАЗУ 2017 Теоретическая механика
2.21 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
Варианты задачи: 2, 3, 4, 5, 6, 7, 8, 9, 10.
ВУЗ: РГАЗУ
2.22 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.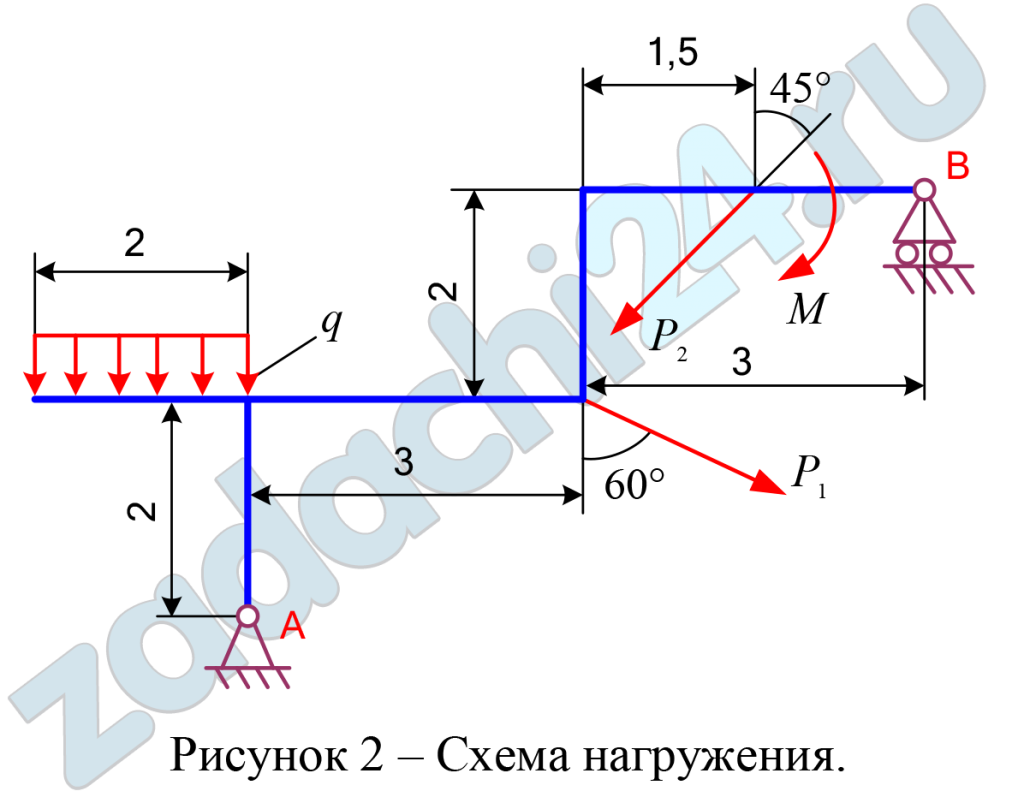
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
Варианты задачи: 2, 3, 4, 5, 6, 7, 8, 9, 10.
ВУЗ: РГАЗУ
2.23 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.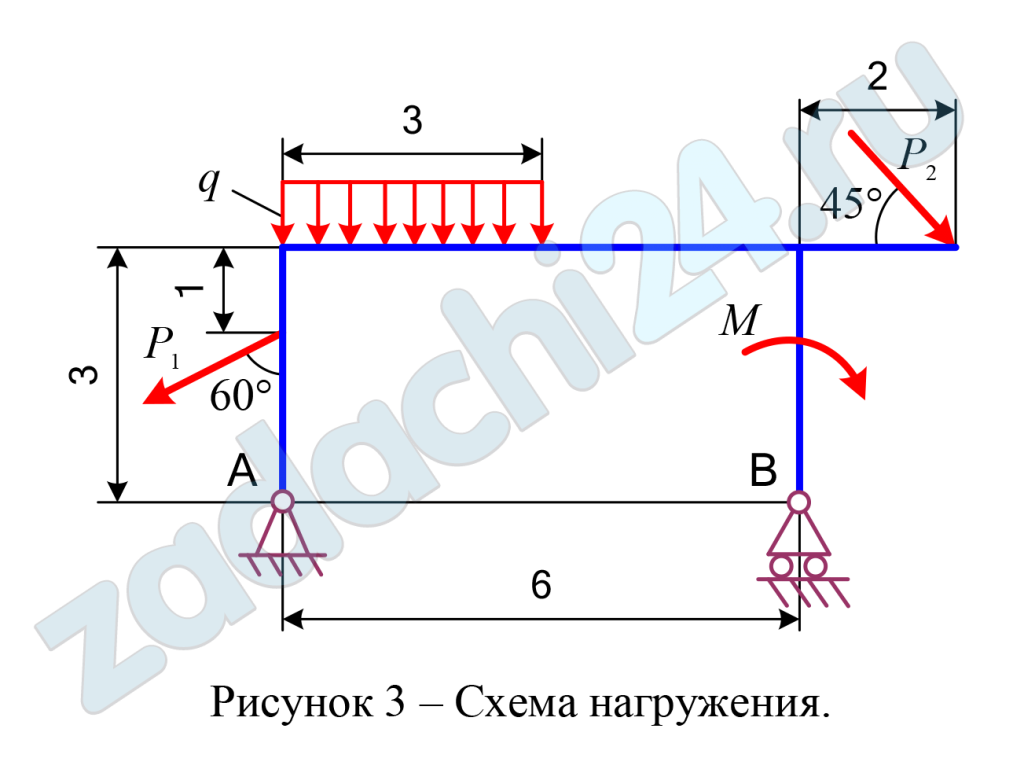
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
Варианты задачи: 2, 3, 4, 5, 6, 7, 8, 9, 10.
ВУЗ: РГАЗУ
2.24 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.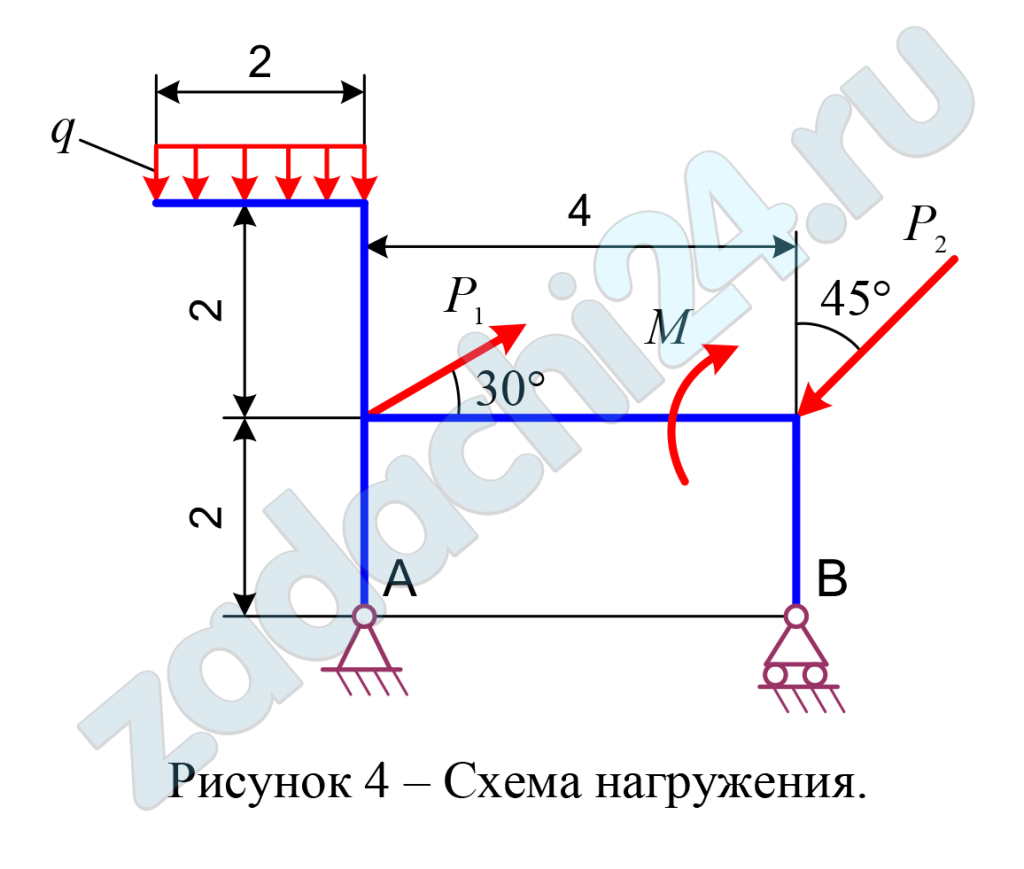
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
Варианты задачи: 2, 3, 4, 5, 6, 7, 8, 9, 10.
ВУЗ: РГАЗУ
2.25 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.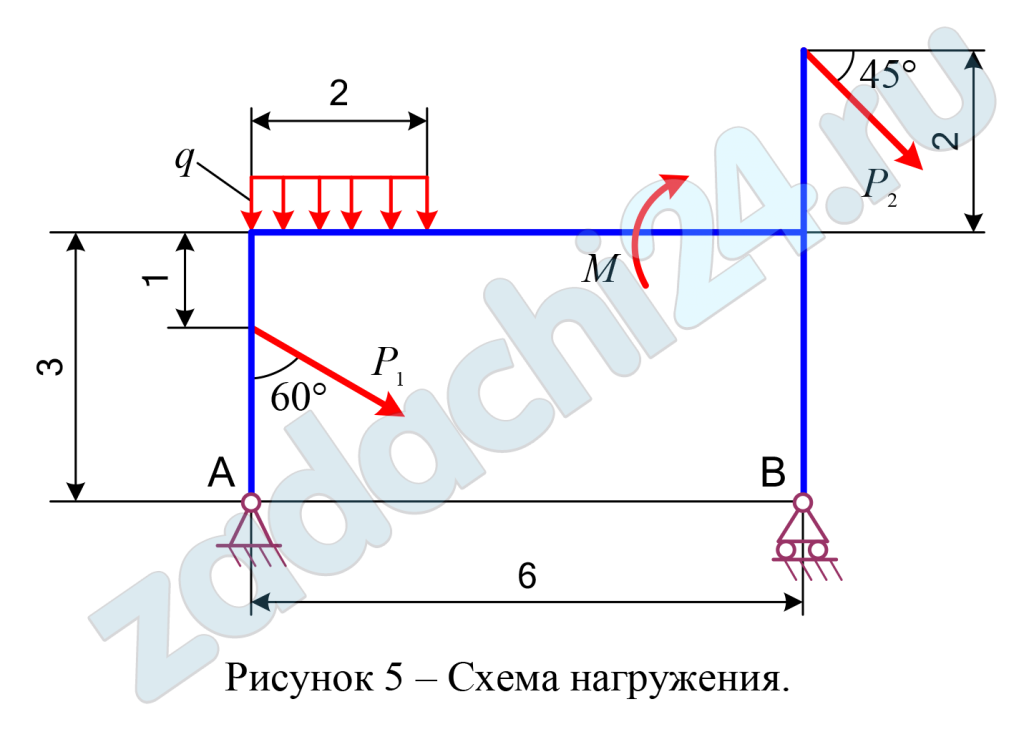
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
Варианты задачи: 2, 3, 4, 5, 6, 7, 8, 9, 10.
ВУЗ: РГАЗУ
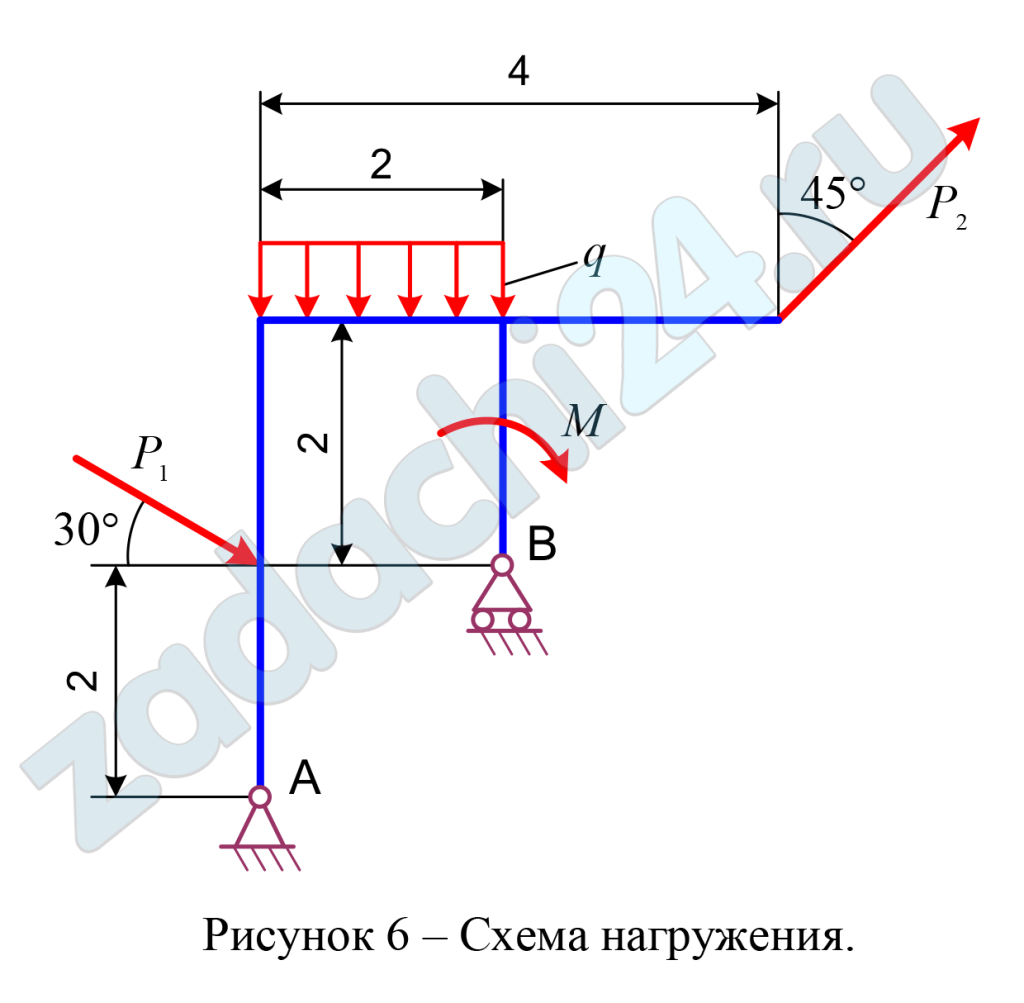
2.26 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
Варианты задачи: 2, 3, 4, 5, 6, 7, 8, 9, 10.
ВУЗ: РГАЗУ
2.27 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.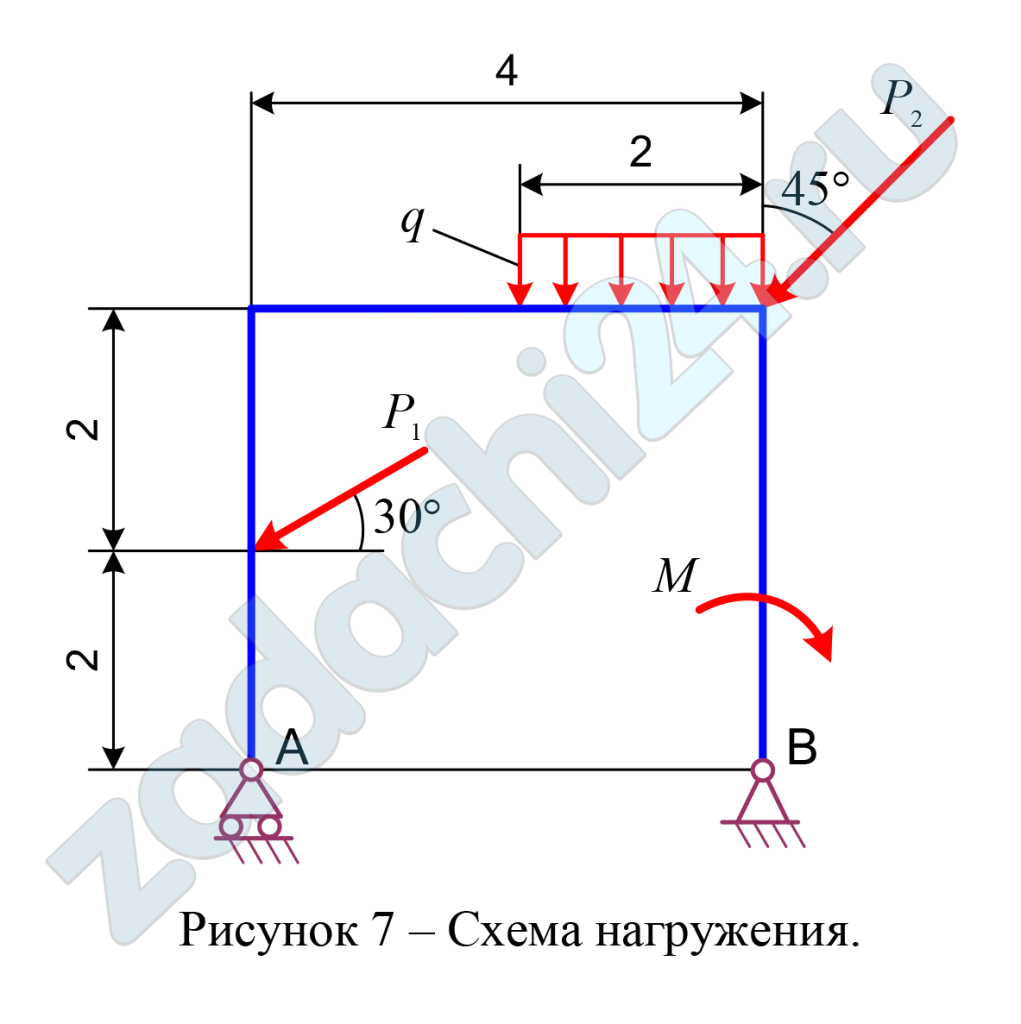
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
ВУЗ: РГАЗУ
2.28 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.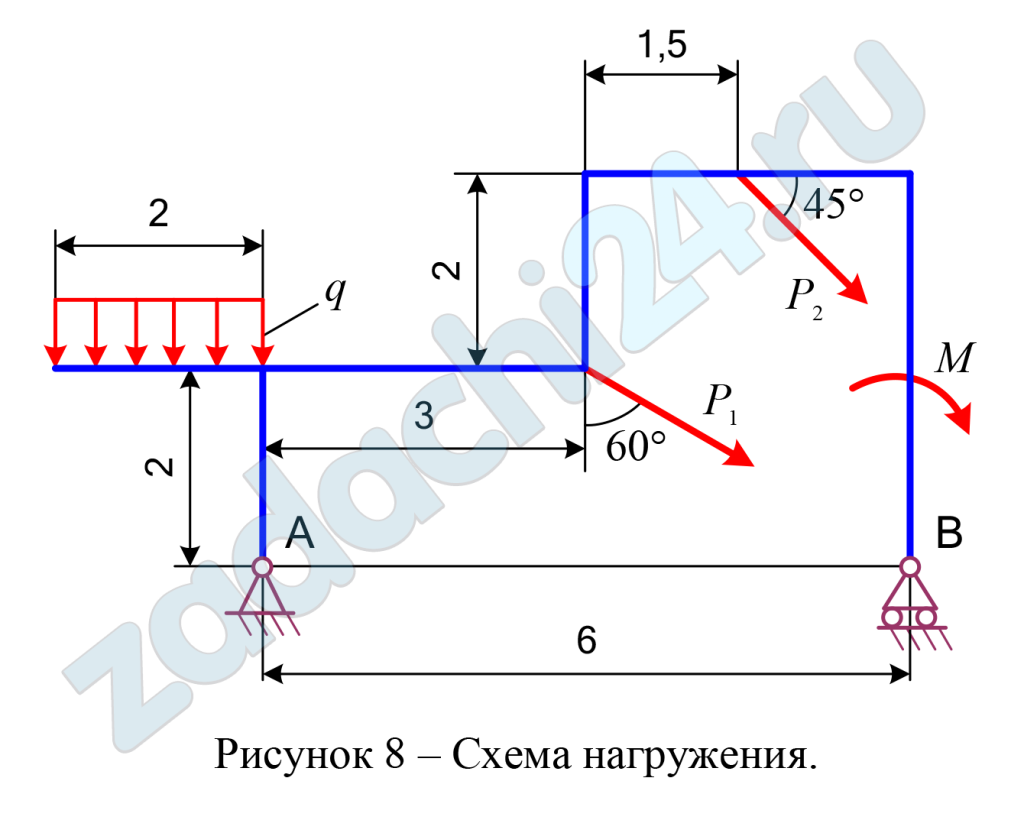
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
ВУЗ: РГАЗУ
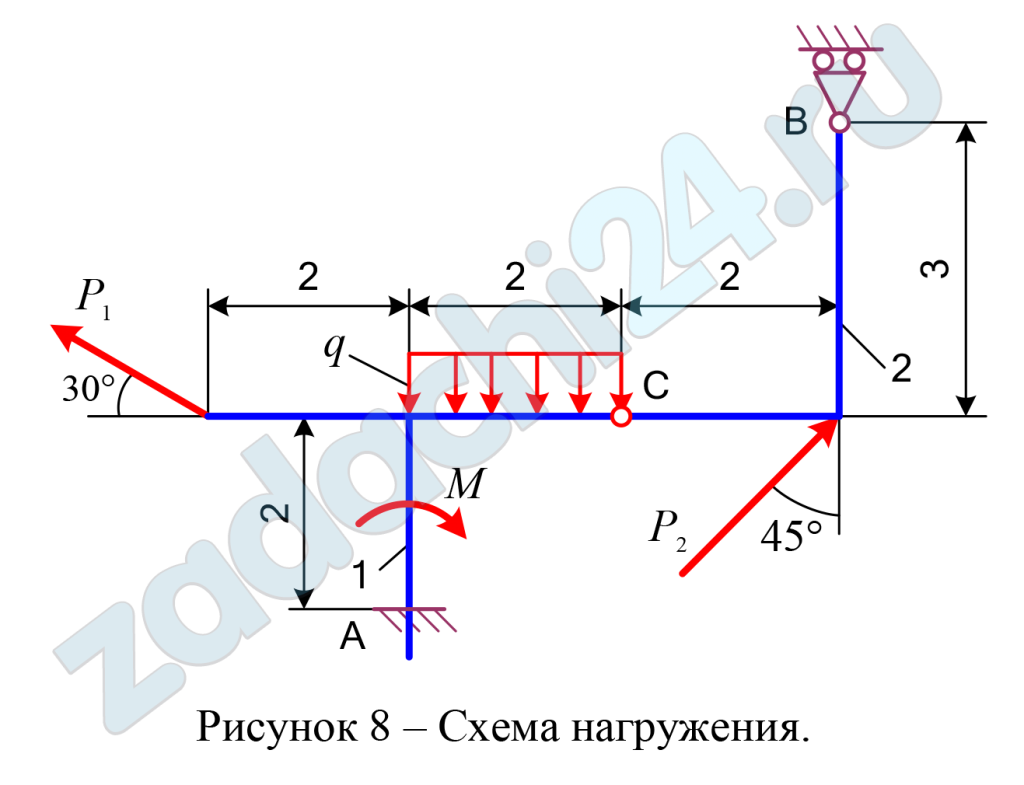
2.38 Определение реакций опор составной конструкции
Для составной конструкции АВС определить реакции опор А и В, возникающие под действием сосредоточенных сил Р1 и Р2, алгебраического момента пары сил М и равномерно распределенной нагрузки интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 7.
Таблица 7 – Исходные данные к задаче 2.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
ВУЗ: РГАЗУ
2.29 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.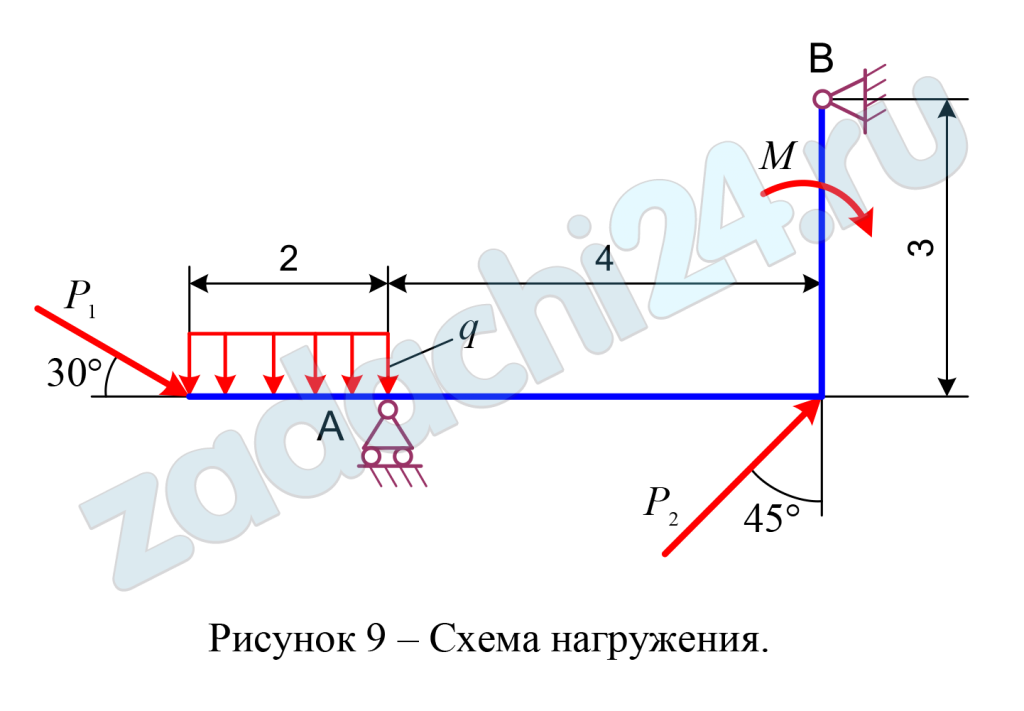
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
ВУЗ: РГАЗУ