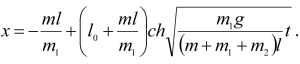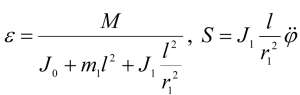Мещерский И.В. Сборник задач по теоретической механике Москва 1986
14.1 Три груза массы М каждый соединены нерастяжимой нитью, переброшенной через неподвижный блок А. Два груза лежат на гладкой горизонтальной плоскости, а третий груз подвешен вертикально. Определить ускорение системы и натяжение нити в сечении ab. Массой нити и блока пренебречь.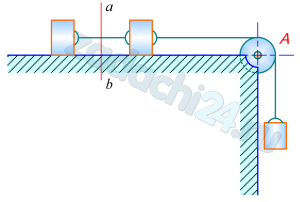
Ответ: a=(1/3)g, T=(1/3)Mg.
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
14.2 Решить предыдущую задачу с учетом массы блока, считая, что при движении грузов блок А вращается вокруг неподвижной оси. Масса блока – сплошного однородного диска – равна 2М.
Ответ: a=(1/4)g, T=(1/4)Mg.
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
13.7 Найти массы М1 и М2 двух грузов, удерживаемых в равновесии грузом массы М на плоскостях, наклоненных к горизонту под углами α и β, если грузы с массами М1 и М2 прикреплены к концам троса, идущего от груза с массой М1 через блок О1, насаженные на горизонтальную ось, к подвижному блоку О, и затем через блок О2, насаженный на ось блока О1 к грузу массы М2. Блоки О1 и О2 — соосные. Трением, а также массами блоков и троса пренебречь.
Ответ: М1=М/2sinα, M2=2/sinβ.
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
16.2 Барабан Б центрифуги приводится во вращение электродвигателем ЭД через двухступенчатый редуктор. Заданы момент инерции J0 электродвигателя, момент инерции J2 барабана, момент инерции J1 промежуточного вала редуктора, передаточные числа i01 и i12 ступеней редуктора. К ротору электродвигателя приложены вращающий момент M0 и момент сопротивления M′0, к валу редуктора и к барабану – моменты сил сопротивления M′1 и M′2, соответственно. Составить дифференциальное уравнение вращения барабана центрифуги.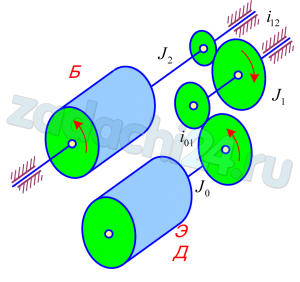
Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
16.3 Определить движение груза массы m, висящего на однородном тросе массы m1 и длины l. Трос навернут на барабан радиуса a и массы m2. Ось вращения горизонтальна. Трением пренебречь. Массу барабана считать равномерно распределенной по его ободу. В начальный момент t=0 система находилась в покое, длина свисавшей части троса l0.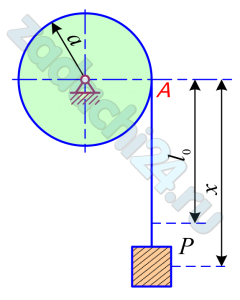
Ответ:
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
16.4 В эпициклическом механизме бегающая шестеренка радиуса r1 насажена на кривошип с противовесом, который вращается вокруг оси неподвижной шестеренки под действием приложенного момента M. Определить угловое ускорение вращения кривошипа и окружное усилие S в точке касания шестеренок, если расстояние равно l, момент инерции кривошипа с противовесом относительно оси вращения кривошипа равен J0, масса бегающей шестеренки m1, момент инерции шестеренки относительно ее оси J1. Трением пренебречь; центр масс шестеренки и кривошипа с противовесом находится на оси вращения кривошипа.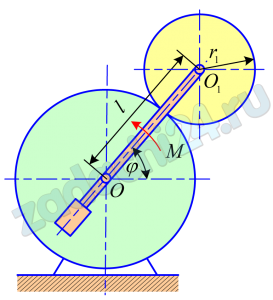
Ответ:
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf