Горюнов С.В. Семенов В.А. РГАЗУ 2017 Теоретическая механика
2.30 Определение реакций опор твёрдого тела
Определить реакции опор А и В плоской балки, если на нее действуют сосредоточенные силы Р1 и Р2, алгебраический момент пары сил М и равномерно распределенная нагрузка интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 6.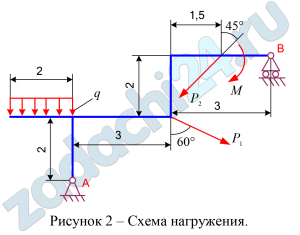
Таблица 6 – Исходные данные к задаче 1.
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
Ответ: ХА=7,24 кН, YA=16,03 кН, Y RА=17,59 кН, YВ=6,17 кН.
2.31 Определение реакций опор составной конструкции
Для составной конструкции АВС определить реакции опор А и В, возникающие под действием сосредоточенных сил Р1 и Р2, алгебраического момента пары сил М и равномерно распределенной нагрузки интенсивностью q.
Схемы нагружения десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 7.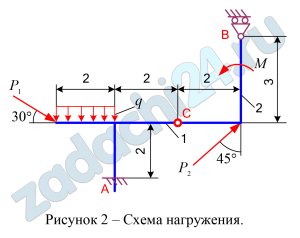
Таблица 7 – Исходные данные к задаче 2
| Вариант | Р1, кН | Р2, кН | q, кН/м | М, кН·м |
| 1 | 8 | 20 | 2 | 8 |
Ответ: ХА=21,16 кН, YА=12,00 кН, МА=38,32 кН·м, YС=4,00 кН, ХС=14,20 кН.
Варианты задачи: 6.
6.14 Определение скорости и ускорения точки по заданным уравнениям её движения
По закону движения точки М на неподвижной плоскости, заданному в координатном виде, требуется установить вид её траектории и для момента времени t1=1 с найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории. Уравнения движения точки М в координатном виде по вариантам приведены в таблице 8.
Таблица 8 – Исходные данные к задаче 3
| Вариант | Уравнения движения | |
| 2 | x=-cos(π/3·t2)+3 | y=sin(π/3·t2)-1 |
Ответ: х=2,50 см, у=-0,13 см, υх=1,81 см/c, υу=1,05 см/c, υ=2,09 см/c, ах=4,00 см/c², ау=-2,75 см/c², а=4,86 см/c², аτ=1,49 см/c², ан=4,63 см/c², ρ=1 см.
Варианты задачи: 3.
7.9 Кинематический анализ плоского механизма
Кривошип 1 вращается относительно оси 4 шарнира О и приводит в движение шатун 2 и ползун на конце шатуна 3, движущегося в направляющих 5. Для расчётного положения плоского механизма требуется найти модули скоростей точек А, В и С и модули угловых скоростей звеньев этого механизма.
Схемы плоских механизмов десяти типов даны на рисунках под номерами от 1 до 10, а числовые данные для расчета приведены в таблице 9.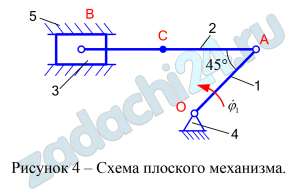
Таблица 9 – Исходные данные к задаче 4
| Вариант | φ1, рад/с | ОА, м | АВ, м | АС, м |
| 1 | 1 | 40 | 80 | 40 |
Ответ: υА=40 м/c, υВ=28 м/c, υС=31,15 м/c, φАВ=0,35 рад/с.
Варианты задачи: 6.
11.5 Определение ускорения движения центра масс груза
Каток 1 массой m1, на который намотан нерастяжимый канат, катится без скольжения по горизонтальной плоскости из состояния покоя под действием момента Μ пары сил и поднимает канатом, перекинутым через блок 2 массой m2, груз 3 массой m3 по наклонной плоскости, образующей угол α с горизонтом (рис. 1). Пренебрегая трением качения катка с плоскостью и проскальзыванием нити относительно блока и катка, найти ускорение движения центра масс груза. Принять, что каток и блок представляют собой сплошные однородные цилиндры радиусами R1 и R2, участок каната между катком и блоком горизонтальный и коэффициент трения скольжения при движении груза по плоскости равен μ. Исходные данные приведены в таблице 10.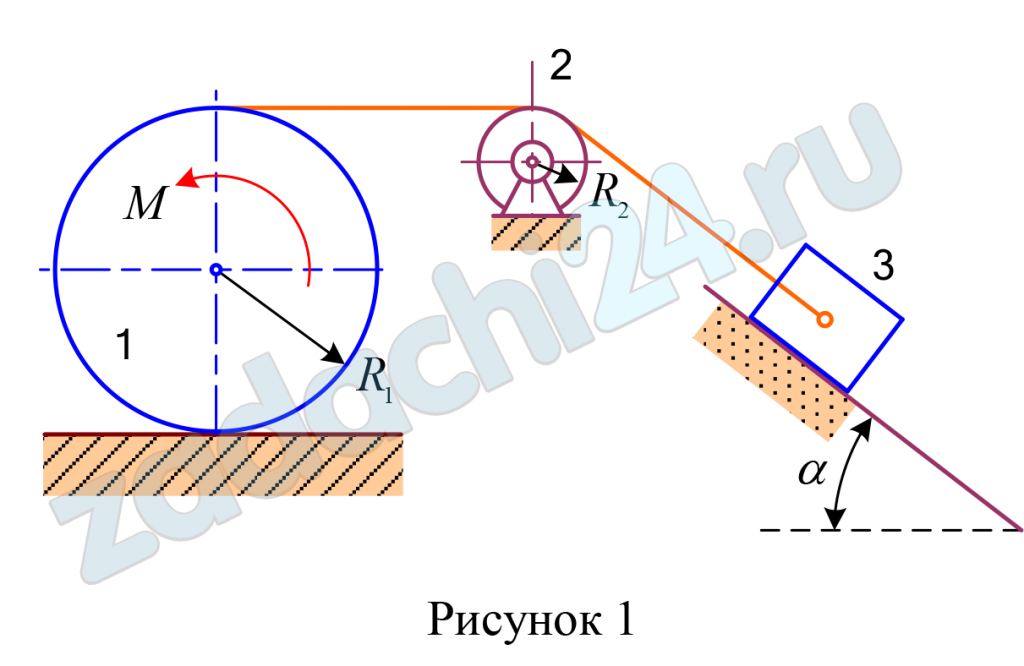
Таблица 10 – Исходные данные к задаче 5.
| Вариант 2 | |||||||
| α, º | μ | R1, м | R2, м | М, Н·м | m1, кг | m2, кг | m3, кг |
| 60 | 0,2 | 0,2 | 0,6 | 22 | 40 | 10 | 14 |
Ответ: аА=3,4 м/c².
