9 Гидравлические сопротивления

9.181  Путём измерения установлено, что в трубопроводе диаметром d = 0,075 м осевая скорость υ_макс =1,0 м/c. Вязкость жидкости μ = 0,03 Н·с/м², плотность ρ = 850 кг/м³. Определить гидравлический уклон J.

9.182 По трубопроводу диаметром d = 102 мм, длиной l = 300 м необходимо перекачать Q = 36 м³/час воды. Определить требуемое давление насоса с таким расчётом, чтобы в конечной точке водопровода иметь пьезометрический напор h = 12 м. Трубопровод стальной, при необходимости эквивалентную шероховатость принять k_экв = 0,14 мм.

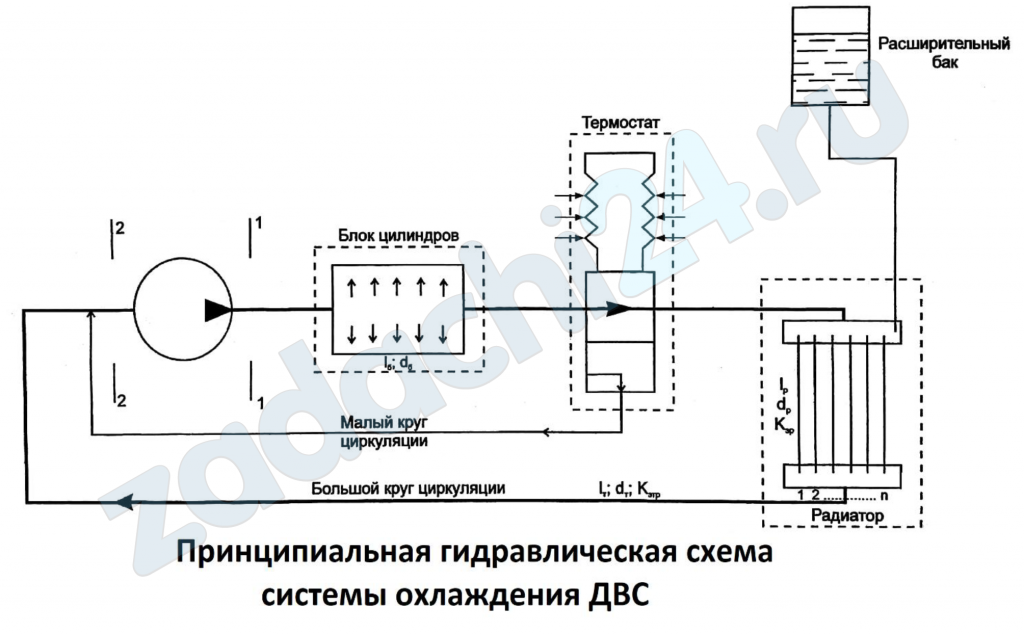
9.183 Расчет гидравлической схемы системы охлаждения ДВС Вариант 3

Дано:

Количество трубок радиатора n = 95;

Диаметр трубок радиатора d_р = 7 мм;

Длина трубок радиатора l = 490 мм;

Диаметр трубопровода d_тр = 37 мм;

Количество изгибов трубопровода 4;

ΔТ = 11ºК;

М = 40 кВт;

l_б = 2,5 м;

L = 2 м;

N_н = 1,5 кВт;

η_н = 0,2;

Удельная теплоёмкость при постоянном давлении С_р = 4190 Дж/(кг∙К).

Коэффициенты местных сопротивлений:

— на вход в верхний бачок радиатора ξ_в = 1,0;

— на вход в трубку радиатора ξ_р = 0,5;

— на выход из трубки радиатора в нижний бачок ξ_вых = 1,0;

— на выход из нижнего бачка ξ_выхт = 0,5;

— рубашки охлаждения блока цилиндров ξ_бц = 5;

— термостата ξ_т = 3;

— изгиба трубопровода ξ_изг = 0,2.

Эквивалентная шероховатость трубок радиатора Δ_р = 0,01 мм.

Эквивалентная шероховатость трубопровода Δ_т = 0,05 мм.

Кинематический коэффициент вязкости охлаждающей жидкости ν = 0,39 10^-6 м² /с.

Плотность охлаждающей жидкости ρ = 975 кг/м³ .

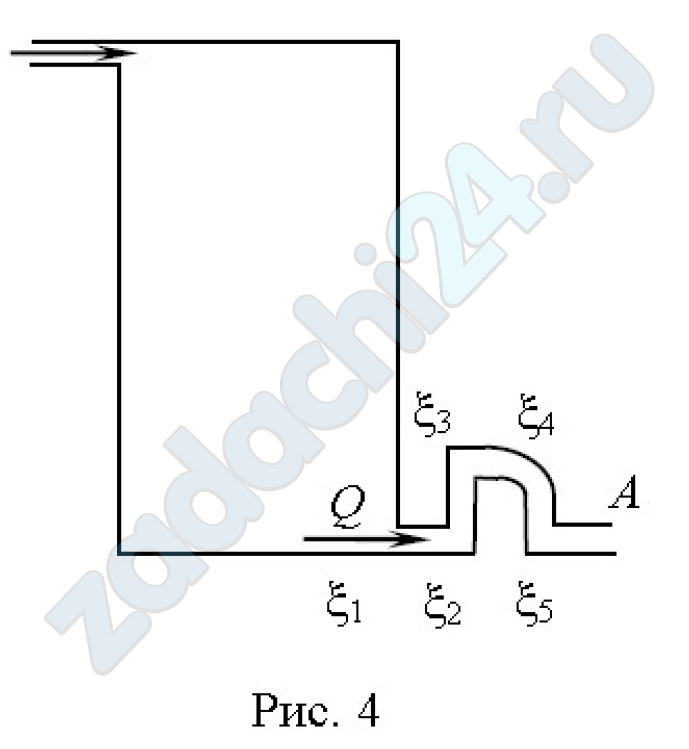
9.184 Через резервуар пропускается постоянный расход жидкости Q (рис. 4). Определить местные потери давления в коротком трубопроводе. Суммарный коэффициент местных сопротивлений:

ξ = ξ₁ + ξ₂ + ξ₃ + ξ₄ + ξ₅;

Q = 26 л/мин, d = 13 мм, ξ = 7, ν_ж = 45×10^-6 м²/с, ρ = 860 кг/м³.

9.185 С целью опытного определения эквивалентной шероховатости стального трубопровода диаметром d = 0,10 м была измерена потеря напора на участке длиной l = 9,4 м. При перекачке по трубопроводу расхода Q = 7,85×10^-2 м³/с воды потеря напора на указанном участке оказалась равной h_тр = 7,8 м. Вычислить эквивалентную шероховатость k_экв.

9.186 Определить потерю напора h_тр в нефтепроводе диаметром d = 0,152 м, длиной l = 2100 м при движении нефти со средней скоростью υ = 2,9 м/c. Вязкость нефти ν = 0,8×10^-4 м²/c. Обосновать выбор формулы. Каких данных не хватает в условии для определения возможности возникновения гидравлического удара?

9.187 По трубопроводу диаметром d = 207 мм перекачивается жидкость, вязкость которой равна ν = 0,37 ст. Расход Q = 24 л/с, длина трубопровода l = 300 м. На трубопроводе имеются местные сопротивления: один отвод литой чугунный, изогнутый по радиусу R = 300 мм, и одна задвижка. Определить приведённую длину трубопровода L в случаях: а) когда задвижка открыта; б) когда задвижка прикрыта на половину.

9.188 Определить длину трубопровода, если скорость потока жидкости v = 1,24 м/c, потеря напора h = 2,8 м, диаметр трубопровода d = 31 мм, коэффициент динамической вязкости μ = 1,48×10^-3 Па·с, плотность ρ = 888 кг/м³.

9.189 Определить скорость потока жидкости по трубопроводу длиной L = 467 м и диаметром d = 43 мм, если потеря напора составила h = 0,284 м, температура t = 45 ºС, коэффициент кинематической вязкости ν = 1,65×10^-6 м²/с. Движение потока жидкости ламинарное. Значение скорости определить с точностью до    3-х значащих цифр.

9.190 Определить потерю напора h_f в водопроводе диаметром d = 76 мм, длиной L = 1300 м при перекачке Q = 7,3 л/сек воды. На трубопроводе имеются местные сопротивления: один вентиль; один всасывающий клапан и колено, сваренное под углом α = 45°. Вычислить какую часть общих потерь напора составляет потеря напора на местных сопротивлениях. Эквивалентная шероховатость труб k_экв = 0,14 мм.