8 Сложное движение точки

8.11 СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ

По заданным уравнением относительного движения точки М неровного движения тела Д определить для момента времени t=t₁ абсолютную скорость и абсолютное ускорение точки M.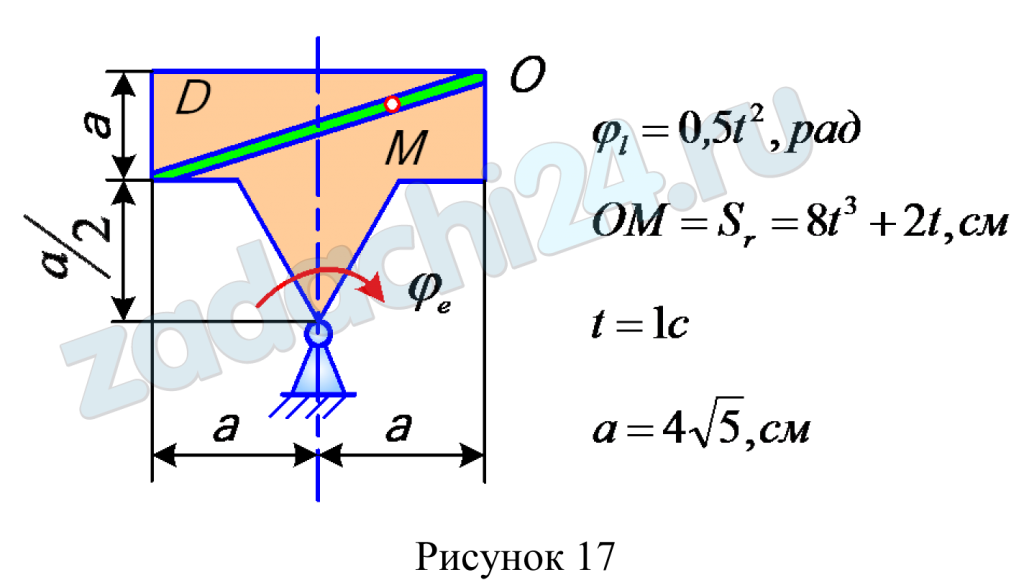

8.12 ДВИЖЕНИЕ ТОЧКИ ОТНОСИТЕЛЬНО ДВУХ СИСТЕМ ОТСЧЕТА, ПЕРЕМЕЩАЮЩИХСЯ ОДНА ОТНОСИТЕЛЬНО ДРУГОЙ

Варианты 1-5. Диск D вращается вокруг неподвижной оси  так, что уравнение ее вращательного движения имеет вид: φ = kt², φ = (,), где k – заданная постоянная величина. По пластинке, по дуге ABC окружности радиусом R, движется точка M так, что траекторная координата этого движения изменяется согласно уравнению s = a + bt + ct², где a, b, c – заданные постоянные величины (траекторная координата отсчитывается от точки H). Определить скорость и ускорение точки M относительно неподвижной системы отсчёта Oxyz в момент времени t = t₁.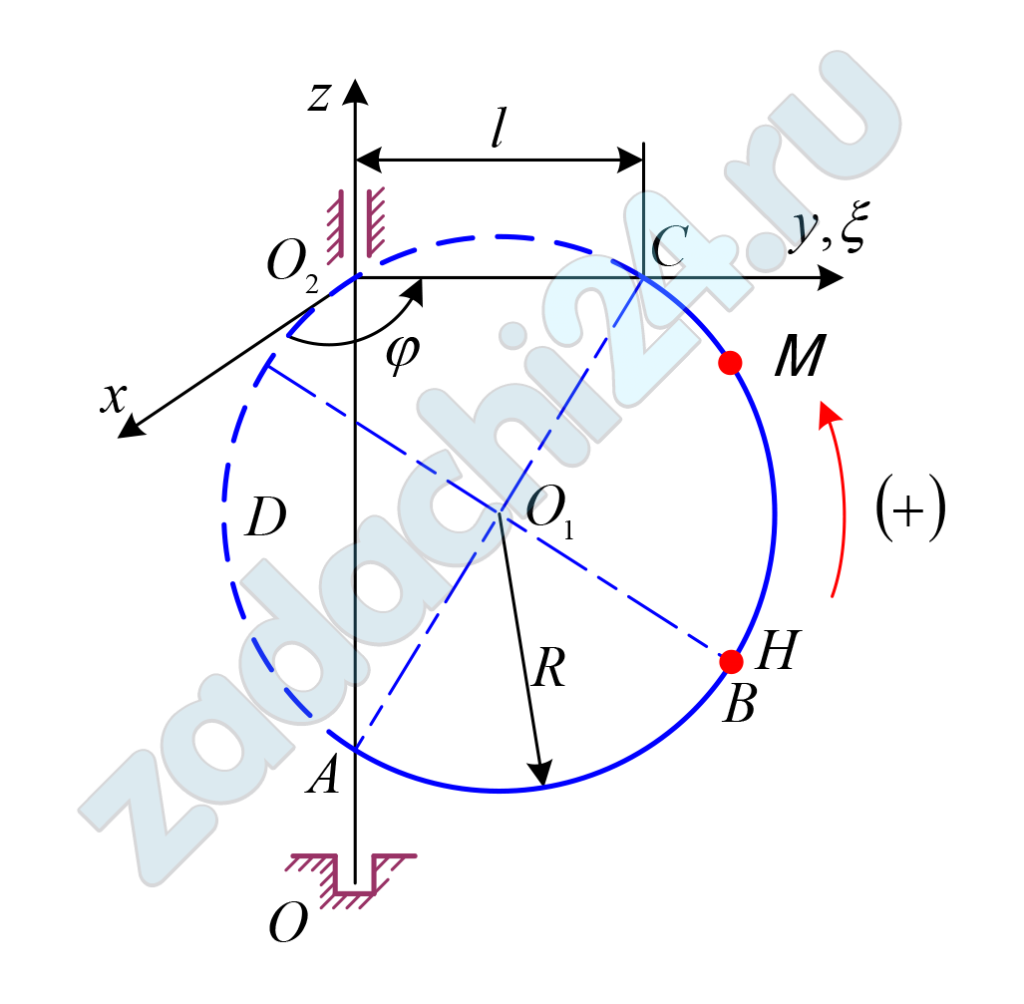

Исходные данные