6 Равновесие жидкости в движущихся сосудах
6.1 В цилиндрический сосуд (схема 1.10) диаметром D0=0,3 м и высотой Н0=0,5 м налита вода с начальным уровнем hн=0,3 м. Определить: 1) Будет ли выплескиваться вода, если сосуд будет вращаться с постоянной частотой вращения n? 2) На каком расстоянии z0 от дна будет находиться самая низшая точка свободной поверхности? 3) С какой частотой нужно вращать сосуд, чтобы вода поднялась до краев сосуда?
Ответ: 1) вода выливаться не будет; 2) z0=0,253 м ; 3) ω=18,7 рад/c.
6.2 Топливный бак автомобиля длиной L=0,6 м, шириной b=0,5 м и высотой Н=0,2 м движется с ускорением а=3,27 ²м/с. Определить минимальное количество топлива в баке, обеспечивающее его подачу без подсоса воздуха. Считать, что бензопровод установлен в центре горизонтальной проекции бака, его диаметр мал по сравнению с длиной бака, h=10 мм.
Ответ: W=9,1 л.
Учебник: Задачник по гидравлике, гидромашинам и гидроприводу. Под ред. Б.Б. Некрасова.pdf
6.3 Цилиндрическая цистерна наполнена бензином, температура которого 20ºC. Диаметр цистерны D, длина L. Глубина бензина в горловине h=20 см, ее диаметр d=30 см. Определить силы давления на плоские торцевые стенки А и В цистерны в двух случаях: 1) когда цистерна не движется; 2) при движении цистерны горизонтально с положительным ускорением а.
Таблица 1
| Вариант | D, м | L, м | a, м/c2 |
| 1 | 2,24 | 4,08 | 7,20 |
Ответ: 1) F=38 кН, 2) FA=73,7 кН, FB=8,1 кН.
6.4 Цилиндрический закрытый сосуд (рис. 13, табл. 3) с вертикальной осью, имеющий высоту H и диаметр 2R, наполнен жидкостью на глубину H0. Определить скорость его вращения (число оборотов в минуту) в двух случаях: а) когда воронка расположена на высоте h над дном сосуда; б) когда диаметр воронки равен 2r.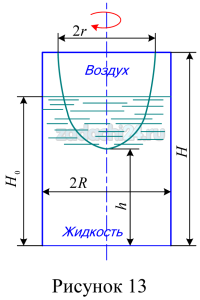
Таблица 3
| Вариант | Н, мм | Н0, мм | R, мм | h, мм | r, мм |
| 1 | 1000 | 600 | 100 | 0 | 100 |
Ответ: ω1=2952 об/мин, ω2=2382 об/мин.
6.5 Сосуд в виде прямоугольного параллелепипеда с размерами L B H до высоты 2/3H заполнен водой, температура которой 20 ºC. Определить, с каким наибольшим положительным ускорением a может двигаться сосуд по наклонной плоскости под углом α, чтобы вода не выливалась, и какие силы давят на торцовые стенки сосуда в случаях: а) при движении сосуда вниз (рисунок 21, а); б) при движении сосуда вверх (рисунок 21, б).
Указание. Ускорение a определяется по формуле tgβ=a·cosα/(g-a·sinα), где β — угол между поверхностью жидкости и горизонтальной плоскостью; g — ускорение силы тяжести.
Таблица 9 – Исходные данные
| Вариант | L, м | В, м | Н, м | αº |
| к | 2,40 | 1,20 | 1,30 | 8 |
Ответ: а) а=4,8 м/c², Рл=11 кН, Рпр=16,3 кН; б) а=1,3 м/c², Рл=10,0 кН, Рпр=5,5 кН.
Варианты задачи: в.
Все задачи из: Гидравлика УГНТУ Салават 2017
6.6 Цилиндрическая цистерна наполнена авиационным бензином, температура которого 20 ºС. Диаметр цистерны D, длина L. Определить силы давления на плоские торцевые стенки А и В цистерны в двух случаях: 1) когда цистерна не движется; 2) при движении цистерны горизонтально с положительным ускорением а. Данные, необходимые для решения задачи, в соответствии с вариантом задания выбрать из табл.9.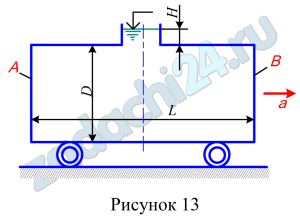
Таблица 1
| Вариант | D | L | H | а, м/c2 |
| м | ||||
| д | 1,74 | 3,25 | 0,22 | 5,42 |
Ответ: 1) F=19 кН, 2) FA=35 кН, FB=1,1 кН.
6.7 В литейную форму, вращающуюся относительно горизонтальной оси, залита расплавленная бронза. Определить минимальную частоту вращения формы, при которой разностенность, вызванная влиянием сил тяжести, была бы не более 1 мм. Каково будет соотношение сил инерции и тяжести при среднем радиусе внутренней поверхности отливаемой втулки 100 мм (рис. 6.41)?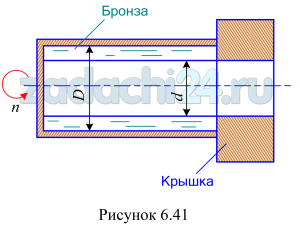
Ответ: n=946 об/c, j=980,39 м/с²>>g.
6.8 Определить силу давления воды на полусферическую крышку цилиндрического сосуда радиусом R=0,2 м, если сосуд вращается относительно своей горизонтальной оси с угловой скоростью ω=100 с-1, а избыточное давление в точке А ри=50 кПа (рис. 6.55).
Ответ: Р=6293 Н.
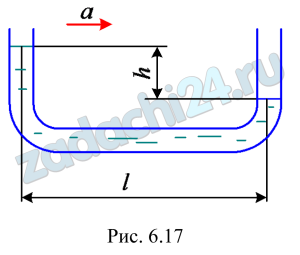
6.9 Определить силу, отрывающую полусферическую поверхность от цилиндрического сосуда, если R=0,2 м, а угловая скорость вращения сосуда относительно своей вертикальной оси ω=100 с-1. Избыточное давление в точке А ри=50 кПа. Жидкость — вода (рис. 6.57).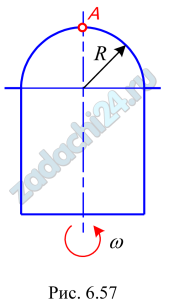
Ответ: Р=26,1 кН.
6.10 Для измерения ускорения горизонтально движущегося тела может быть использована закрепленная на нем U-образная трубка малого диаметра, наполненная жидкостью (рис. 6.17). С каким ускорением а движется тело, если при движении установилась разность уровней жидкости в ветвях трубки h=10 см при расстоянии между ними l=20 см?
Ответ: а=4,9 м/с².
