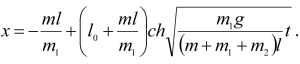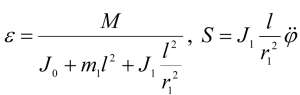16 Уравнения Лагранжа
16.1 ЗАДАНИЕ Д-9
Уравнения Лагранжа II рода
Для заданной механической системы на основе уравнений Лагранжа II рода составить дифференциальные уравнения движения. Необходимые данные и рекомендуемые обобщенные координаты приведены в таблице Д-9.
При решении задачи массами нитей пренебречь. Считать, что качение происходит без проскальзывания. Блоки и катки, для которых в таблице радиусы инерции не указаны, считать сплошными однородными цилиндрами. Силы сопротивления в подшипниках не учитывать. Заданные силы P и моменты пар M считать постоянными величинами.
Таблица Д-9
| № варианта | № рисунка | m1 | m2 | m3 | m4 | m5 | Р |
| 6 | 6 | m1 | m2 | m3 | m4 | m5 | — |
Продолжение Таблицы Д-9
| М | f | k | q1 | q2 | ρ | α | Дополнительные указания |
| — | — | — | x | ξ | 2r | — | ρ – радиус инерции тела 3 |
ВУЗ: Московский Политех
Все задачи из: Теоретическая механика Московский Политех
16.2 Барабан Б центрифуги приводится во вращение электродвигателем ЭД через двухступенчатый редуктор. Заданы момент инерции J0 электродвигателя, момент инерции J2 барабана, момент инерции J1 промежуточного вала редуктора, передаточные числа i01 и i12 ступеней редуктора. К ротору электродвигателя приложены вращающий момент M0 и момент сопротивления M′0, к валу редуктора и к барабану – моменты сил сопротивления M′1 и M′2, соответственно. Составить дифференциальное уравнение вращения барабана центрифуги.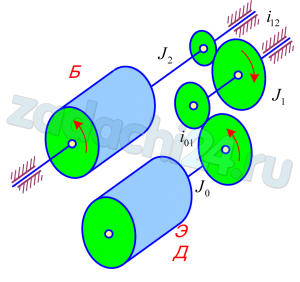
Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
16.3 Определить движение груза массы m, висящего на однородном тросе массы m1 и длины l. Трос навернут на барабан радиуса a и массы m2. Ось вращения горизонтальна. Трением пренебречь. Массу барабана считать равномерно распределенной по его ободу. В начальный момент t=0 система находилась в покое, длина свисавшей части троса l0.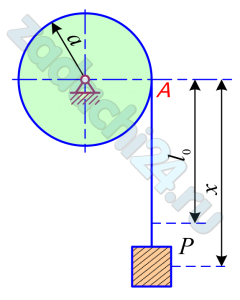
Ответ:
Скачать файл (банки РФ) 120 RUBУчебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
16.4 В эпициклическом механизме бегающая шестеренка радиуса r1 насажена на кривошип с противовесом, который вращается вокруг оси неподвижной шестеренки под действием приложенного момента M. Определить угловое ускорение вращения кривошипа и окружное усилие S в точке касания шестеренок, если расстояние равно l, момент инерции кривошипа с противовесом относительно оси вращения кривошипа равен J0, масса бегающей шестеренки m1, момент инерции шестеренки относительно ее оси J1. Трением пренебречь; центр масс шестеренки и кривошипа с противовесом находится на оси вращения кривошипа.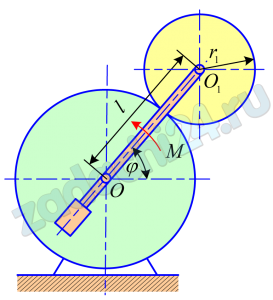
Ответ:
Скачать файл (банки РФ) 150 RUBУчебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf