15 Интегралы движения
15.1 Интегрирование дифференциальных уравнений движения точки, находящейся под действием постоянных сил
Груз М массой m начинает движение из точки D с начальной скоростью V0. Его движение происходит по наклонной плоскости длины l, составляющей угол α с горизонтом вдоль линии АВ наибольшего ската (рис. Д1.0 ÷ Д1.9). Положение точки D задается величиной AD = s0, вектор начальной скорости V0 направлен параллельно прямой АВ к точке В. При движении по плоскости на груз действует постоянная сила Q, направление которой задается углом γ; коэффициент трения скольжения между грузом и наклонной плоскостью равен f. Через τ с груз покидает плоскость или в точке A, или в точке B и, двигаясь далее в вертикальной плоскости под действием только силы тяжести, через T секунд после отделения от плоскости попадает в точку С. Все возможные варианты траекторий движения груза в точку C показаны на рисунках.
Считая груз материальной точкой найти:
– точку (А или В) отрыва груза от плоскости;
– время τ движения груза по наклонной плоскости;
– скорость груза VB (или VA) в момент отрыва;
– координаты xC, yC точки C приземления груза;
– время T движения груза в воздухе;
– скорость VC груза в точке падения.
Таблица Д1
Исходные данные
| Номер условия | l, м | α,º | γ,º | m, кг | s0, м | V0, м/c | Q, Н |
| 1 | 50 | 45 | 30 | 20 | 15 | 15 | 30 |
Оформление готовой работы
ВУЗ: ИРНИТУ
Все задачи из: Теоретическая механика ИРНИТУ
15.2 Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
В железнодорожных скальных выемках для защиты кюветов от попадания в них с откосов каменных осыпей устраивается «полка» DC. Учитывая возможность движения камня из наивысшей точки A откоса и полагая при этом его начальную скорость υ0 равной нулю, определить минимальную ширину полки b и скорость υC, с которой камень падает на нее. По участку AB откоса, составляющему угол α с горизонтом и имеющему длину l, камень движется τ c.
При решении задачи считать коэффициент трения скольжения f камня на участке AB постоянным, а сопротивлением воздуха пренебречь.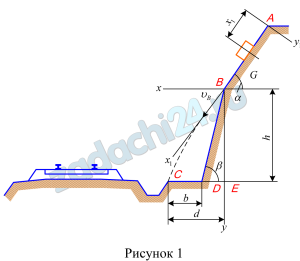
Таблица 1 – Исходные данные
| υА, м/c | α,º | l, м | τ, c | f | h, м | β,º |
| 0 | 60 | 4 | 1 | f≠0 | 5 | 75 |
15.3 Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
Вариант 6 (рис. 117, схема 2). Лыжник подходит к точке А участка трамплина АВ, наклоненного под углом α к горизонту и имеющего длину l, со скоростью υА. Коэффициент трения скольжения лыж на участке АВ равен f. Лыжник от А до В движется τ с; в точке В со скоростью υВ он покидает трамплин. Через Т с лыжник приземляется со скоростью υС в точке С горы, составляющей угол β с горизонтом.
При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха.
Дано: α = 20º; f = 0,1; τ = 0,2 с; h = 40 м; β = 30º. Определить l и υС.
15.4 Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием постоянных сил
Вариант 8 (рис. 117, схема 2). Лыжник подходит к точке А участка трамплина АВ, наклоненного под углом α к горизонту и имеющего длину l, со скоростью υА. Коэффициент трения скольжения лыж на участке АВ равен f. Лыжник от А до В движется τ с; в точке В со скоростью υВ он покидает трамплин. Через Т с лыжник приземляется со скоростью υС в точке С горы, составляющей угол β с горизонтом.
При решении задачи принять лыжника за материальную точку и не учитывать сопротивление воздуха.
Дано: υА = 21 м/с; f = 0; τ = 0,3 с; υВ = 20 м/с; β = 60º. Определить α и d.
15.5 Применение основных теорем динамики к исследованию движения материальной точки
Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости (рис. 135-137). Найти скорость шарика в положениях В и С и давление шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь h0, отделяется от пружины.
Необходимые для решения данные приведены в табл. 42.
Таблица 42
| Номер варианта (рис. 135-137) | m, кг | υА, м/с | τ, с | R, м | f |
| 8 | 0,2 | 1 | 0,5 | 1,5 | 0,15 |
Конец таблицы 42
| α, град | β, град | h0, см | с, Н/см | Величины,
которые требуется определить дополнительно |
| 30 | 60 | 0 | 4 | h |
В задании приняты следующие обозначения: m – масса шарика; υА – начальная скорость шарика; τ – время движения шарика на участке АВ (в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке BD (в вариантах 3, 4, 6, 7, 9 – 13, 15 – 17, 19, 22, 25, 26, 28, 29); f – коэффициент трения скольжения шарика по стенке трубки; h0 – начальная деформация пружины; h – наибольшее сжатие пружины; с – коэффициент жесткости пружины; Н – наибольшая высота подъема шарика; s – путь, пройденный шариком до остановки.
15.6 Интегрирование дифференциальных уравнений движения материальной точки, находящейся под действием переменных сил
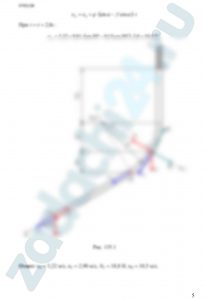
Найти уравнения движения тела М массой m (рис. 119-121), принимаемого за материальную точку и находящегося под действием переменной силы Р = Xi + Yj + Zk, при заданных начальных условиях. Во всех вариантах ось z (где показана) вертикальная, за исключением вариантов 8 и 30.
Необходимые для решения данные приведены в табл. 39, в которой приняты следующие обозначения: i, j, k, — орты координатных осей (соответственно х, у, z); g – ускорение свободного падения (9,81 м/с²); f – коэффициент трения скольжения; t – время, с; х, у, z, х′, у′, z′ — координаты точки и проекции ее скорости на оси координат соответственно, м и м/с.
Во всех случаях, где сила зависит от х, х′, у′, z′, рассмотреть движение точки, при котором эти величины только положительны.
Таблица 39
| Номер варианта (рис. 119-121) | m, кг | , Н | Начальные условия | ||||||
| f | х0 | у0 | z0 | х′0 | у′0 | z′0 | |||
| м | м/c | ||||||||
| 8 | 150 | 0 | 0 | 0 | 0 | 0,5 | 2 | 0 | |
15.7 Применение основных теорем динамики к исследованию движения материальной точки
Шарик, принимаемый за материальную точку, движется из положения А внутри трубки, ось которой расположена в вертикальной плоскости (рис. 135-137). Найти скорость шарика в положениях В и С и давление шарика на стенку трубки в положении С. Трением на криволинейных участках траектории пренебречь. В вариантах 3, 6, 7, 10, 13, 15, 17, 19, 25, 28, 29 шарик, пройдя путь h0, отделяется от пружины.
Необходимые для решения данные приведены в табл. 42.
Таблица 42
| Номер варианта (рис. 135-137) | m, кг | υА, м/с | τ, с | R, м | f |
| 3 | 0,4 | 0 | 2,0 | 0,2 | 0,15 |
Конец таблицы 42
| α, град | β, град | h0, см | с, Н/см | Величины, которые требуется
определить дополнительно |
| 30 | — | 10 | 1 | υD |
В задании приняты следующие обозначения: m – масса шарика; υА – начальная скорость шарика; τ – время движения шарика на участке АВ (в вариантах 1, 2, 5, 8, 14, 18, 20, 21, 23, 24, 27, 30) или на участке BD (в вариантах 3, 4, 6, 7, 9 – 13, 15 – 17, 19, 22, 25, 26, 28, 29); f – коэффициент трения скольжения шарика по стенке трубки; h0 – начальная деформация пружины; h – наибольшее сжатие пружины; с – коэффициент жесткости пружины; Н – наибольшая высота подъема шарика; s – путь, пройденный шариком до остановки.
15.8 ЗАДАНИЕ Д-1 Интегрирование дифференциальных уравнений движения материальной точки
Материальная точка M массой m, получив в точке А начальную скорость V0, движется в изогнутой трубе АВС, расположенной в вертикальной плоскости. Участки трубы или оба наклонные, или один горизонтальный, а другой наклонный. Угол наклона трубы α = 30º.
На участке АВ на материальную точку действует сила тяжести Р, постоянная сила (ее направление указано на рисунках) и сила сопротивления среды R, зависящая от скорости V груза (направлена сила против движения). Трением груза о трубу на участке АВ пренебрегаем.
В точке В материальная точка, не изменяя величины своей скорости, переходит на участок ВС трубы, где на нее действует сила тяжести P, сила трения (коэффициент трения груза о трубу f = 0,2) и переменная сила F, проекция которой FX на ось x приведена в таблице Д-1.
Известно расстояние AB = l или время t1 движения от точки А до точки В. Требуется найти закон движения материальной точки на участке BС: x = f (t).
Таблица Д-1
| № варианта 6 | ||||||||
| Рис. | m, кг | V0, м/c | Q, Н | R, Н | μ | l, м | t1, с | FX, Н |
| 6 | 1,2 | 22 | 2 | μV² | 0,8 | 0,5 | — | 6t |
ВУЗ: Московский Политех
Все задачи из: Теоретическая механика Московский Политех
15.9 ЗАДАНИЕ Д-4
Плоскопараллельное движение твердого тела
Барабан радиуса R весом P имеет проточку (как у катушки) радиуса r = 0,5R (рис.4.1, табл. Д-4). К концам намотанных на барабан нитей приложены постоянные силы и , направления которых определяются углом β. Кроме сил на барабане действует пара с моментом M. При движении, начинающимся из состояния покоя, барабан катится без скольжения по шероховатой наклонной плоскости с углом наклона α так, как показано на рисунках.
Пренебрегая сопротивлением качению, определить закон движения центра масс барабана, т.е. xC = f(t) , и наименьшее значение коэффициента трения fmin о плоскость, при котором возможно качение без скольжения. Барабан рассматривать как сплошной однородный цилиндр радиуса R.
Таблица Д-4
| № варианта | № рисунка | α,º | β,º | F1 | F2 | М |
| 6 | 6 | 0 | 60 | 0,3Р | 0,1Р | 0 |
ВУЗ: Московский Политех
Все задачи из: Теоретическая механика Московский Политех