13 Принцип возможных перемещений
13.1 (Вариант 143) РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 3
Принцип возможных перемещений
Задание: Используя принцип возможных перемещений совместно с принципом освобождения твёрдых тел от связей, определить реакции опор A, B, C, D для системы сочленённых балок и определить значение силы F для механической системы с одной степенью свободы. Исходные данные приведены в таблице №3 и на схемах рис. 4.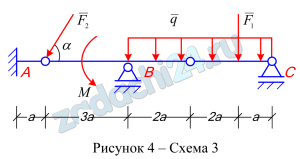
Таблица 3 – Исходные данныt
| Вариант 143 | |||||
| F1, кН | а, м | αº | F2, кН | М, кН·м | q, кН/м |
| 3 | 0,4 | 45 | 3 | 2 | 5 |
13.2 Груз Q поднимается с помощью домкрата, который приводится в движение рукояткой ОА=0,6 м. К концу рукоятки, перпендикулярно ей. приложена сила Р=160 Н.
Определить величину силы тяжести груза Q, если шаг винта домкрата h=12 мм.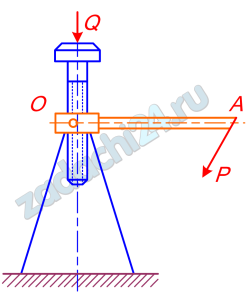
Ответ: Q=50,2 кН.
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
13.3 На маховичок коленчатого пресса действует вращающий момент М; ось маховичка имеет на концах винтовые нарезки шага h противоположного направления и проходит через две гайки, шарнирно прикрепленные к двум вершинам стержневого ромба со стороной a; верхняя вершина ромба закреплена неподвижно, нижняя прикреплена к горизонтальной плите пресса. Определить силу давления пресса на сжимаемый предмет в момент, когда угол при вершине ромба равен 2a.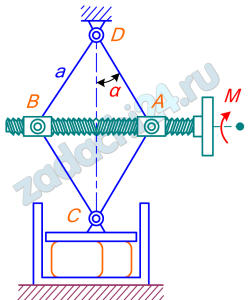
Ответ: P=(πM/h)ctgα.
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
13.4 Определить зависимость между модулями сил P и Q в клиновом прессе, если сила P приложена к концу рукоятки длины a перпендикулярно оси винта и рукоятки. Шаг винта равен h. Угол при вершине клина равен α.
Ответ: Q=P(2πa/htgα).
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
13.5 Рисунок представляет схему машины для испытания образцов на растяжение. Определить зависимость между усилием Х в образце К и расстоянием х от груза Р массы М до его нулевого положения О, если при помощи груза Q машина уравновешена так, что при нулевом положении груза Р и при отсутствии усилия в К все рычаги горизонтальны. Даны расстояния l1, l2 и e.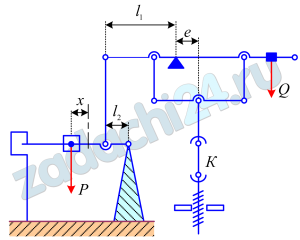
Ответ: X=Mg(xl1/el2).
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
13.6 Полиспаст состоит из неподвижного блока А и из подвижных блоков. Определить в случае равновесия отношение массы М поднимаемого груза к силе Р, приложенной к концу каната, сходящего с неподвижного блока А.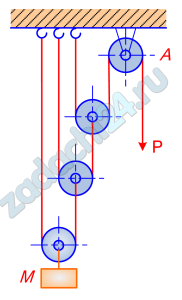
Ответ: Mg/p=2n.
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
13.7 Найти массы М1 и М2 двух грузов, удерживаемых в равновесии грузом массы М на плоскостях, наклоненных к горизонту под углами α и β, если грузы с массами М1 и М2 прикреплены к концам троса, идущего от груза с массой М1 через блок О1, насаженные на горизонтальную ось, к подвижному блоку О, и затем через блок О2, насаженный на ось блока О1 к грузу массы М2. Блоки О1 и О2 — соосные. Трением, а также массами блоков и троса пренебречь.
Ответ: М1=М/2sinα, M2=2/sinβ.
Скачать файл (оплата в RUB)Учебник: Мещерский И.В. Сборник задач по теоретической механике Москва 1986.pdf
13.8 ЗАДАНИЕ Д-7
Принцип возможных перемещений
Механизмы (рис.7.1-7.3) в заданном положении находятся в равновесии. Необходимо определить величину, указанную в предпоследней графе таблицы Д-7.1, применяя принцип возможных перемещений и пренебрегая силами трения. Все необходимые для решения данные приведены в таблице Д-7.1.
Примечание: механизмы в вариантах 3, 6, 10, 14, 16, 18, 19, 25 и 30 расположены в вертикальной плоскости, а остальные — в горизонтальной.
Таблица Д-7.1
| № варианта | Линейный
размеры, см |
Сила Q, Н | Определить | Примечания |
| 6 | r1 = 15;
r2 = 50; r3 = 20; О1А = 80 |
200 | Р | О1А — невесомый |
ВУЗ: Московский Политех
Все задачи из: Теоретическая механика Московский Политех












