11 Динамика материальной системы
11.11 РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА № 2
Теорема об изменении кинетической энергии
Задание: Для заданной механической системы, движение которой начинается из состояния покоя, определить, какую скорость приобретает тело 1 при перемещении на расстояние S.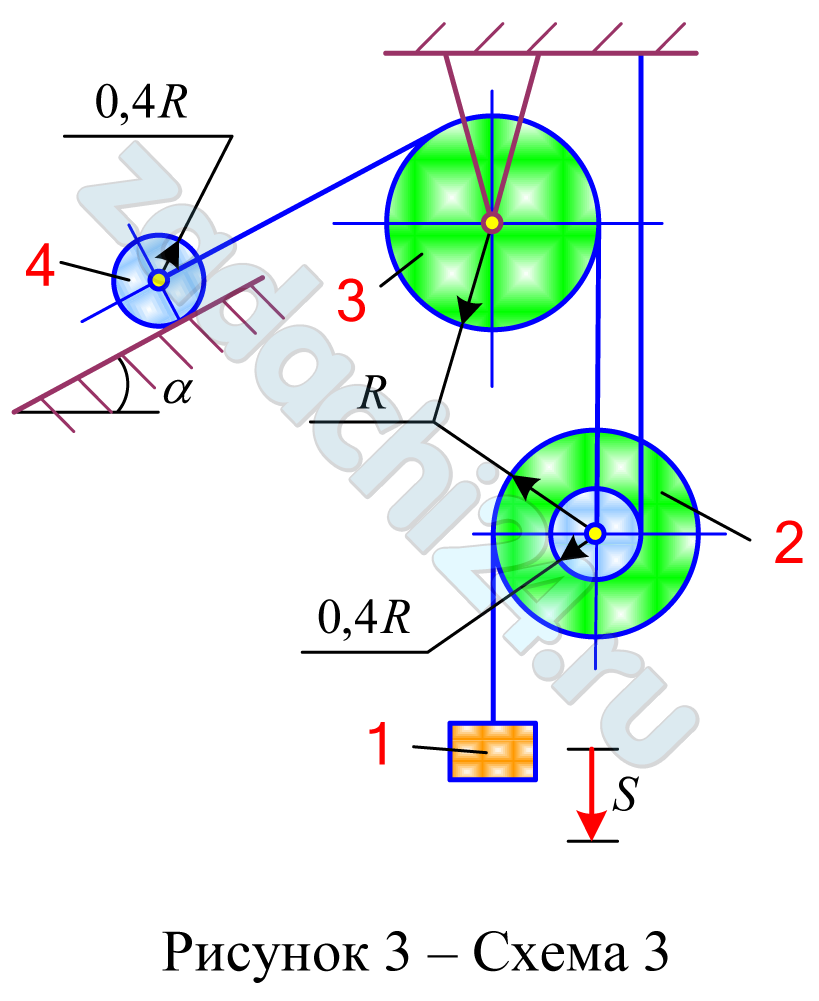
Таблица 2 – Исходные данные
| Вариант 143 | ||||
| m1, кг | R, м | d, м | αº | m2, кг |
| 3m | 0,5 | 0,002 | 45 | 3m |
Продолжение таблицы 2
| f | m3, кг | m4, кг | S1, м | ρ, м |
| 0,1 | 2m | 4m | 5 | 0,15 |
11.12 Определение ускорения движения центра масс груза
Каток 1 массой m1, на который намотан нерастяжимый канат, катится без скольжения по горизонтальной плоскости из состояния покоя под действием момента Μ пары сил и поднимает канатом, перекинутым через блок 2 массой m2, груз 3 массой m3 по наклонной плоскости, образующей угол α с горизонтом (рис. 1). Пренебрегая трением качения катка с плоскостью и проскальзыванием нити относительно блока и катка, найти ускорение движения центра масс груза. Принять, что каток и блок представляют собой сплошные однородные цилиндры радиусами R1 и R2, участок каната между катком и блоком горизонтальный и коэффициент трения скольжения при движении груза по плоскости равен μ. Исходные данные приведены в таблице 10.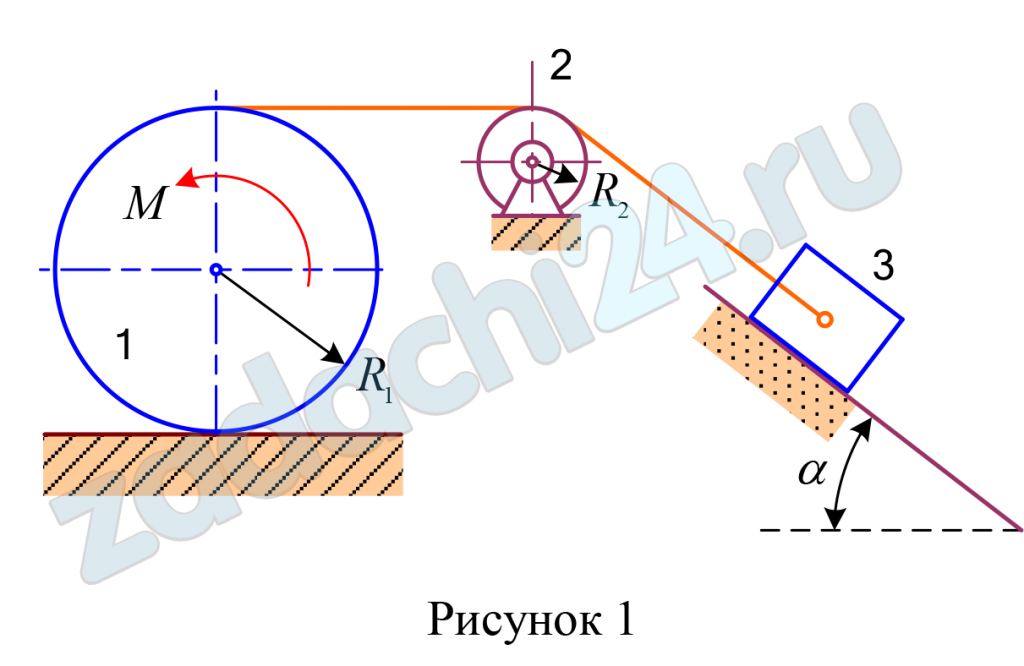
Таблица 10 – Исходные данные к задаче 5.
| Вариант 2 | |||||||
| α, º | μ | R1, м | R2, м | М, Н·м | m1, кг | m2, кг | m3, кг |
| 60 | 0,2 | 0,2 | 0,6 | 22 | 40 | 10 | 14 |
ВУЗ: РГАЗУ
Все задачи из: Горюнов С.В. Семенов В.А. РГАЗУ 2017 Теоретическая механика
11.13 Дифференциальные уравнения движения твердого тела
Механическая система состоит из груза 3 и колес 1 и 2 (рис. 6). К колесу 1 приложена сила P = P(t). Время t отсчитывается от момента t = 0, когда угловая скорость колеса 1 равна ω1,0. Момент сил сопротивления, приложенных к ведомому колесу 2, равен Мс. Другие силы сопротивления движению системы не учитывать. Массы колес 1 и 2 равны m1 и m2, масса груза 3 равна m3. Радиусы больших и малых окружностей колес равны R1, r1, R2, r2. Заданы радиусы инерции i1, i2 тел сложной формы. Если радиус инерции колеса не задан, то считаем его сплошным однородным диском.
Необходимые для решения данные приведены в табл. 3.
Найти закон движения того тела Т системы, номер которого указан в последнем столбце таблицы 3.
Определить также натяжение нити в заданный момент времени t1 и окружное усилие в точке соприкосновения колес 1 и 2.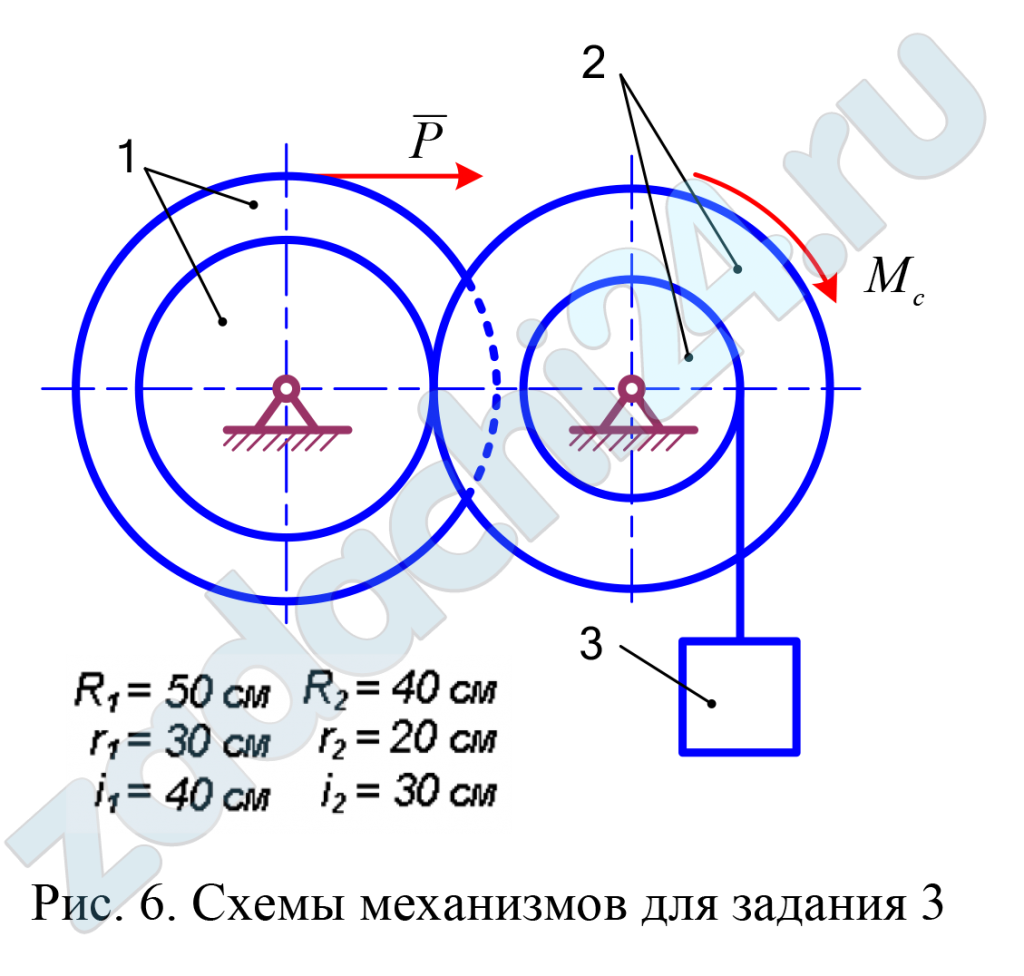
Таблица 3
Исходные данные для задания 3
| Номер варианта 17
Заданные величины |
|||||||
| m1,
кг |
m2,
кг |
m3,
кг |
Р = Р(t),
Н |
Мс,
Н·м |
ω1,0,
рад/c |
t1,
с |
тело Т |
| 150 | 300 | 600 | 5500 + 200t | 1500 | 2 | 1 | 3 |
11.14 Применение теоремы об изменении кинетической энергии к изучению движения механической системы
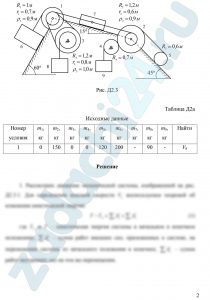
Механическая система состоит из ступенчатых шкивов, колес, блоков 1÷5 и грузов 6÷9 (рис. Д2.0 ÷ Д2.9). На рисунках приняты обозначения: Rk – радиус внешней ступени шкива или радиус тела, rk – радиус внутренней ступени шкива, ρk – радиус инерции тела относительно оси вращения. Для тел 1,2,3 заданы радиусы инерции ρ1, ρ2, ρ3 относительно оси вращения, масса тела 4 равномерно распределена по внешнему ободу, тело 5 считать однородным цилиндром. Тела системы соединены друг с другом гибкими невесомыми нерастяжимыми нитями, которые или перекинуты через блоки, или намотаны на шкивы; участки нитей параллельны соответствующим плоскостям. Некоторые тела соединены ременными или фрикционными передачами.
Радиусы тел и радиусы инерции указаны на рис. Д2.0 ÷ Д2.9. Массы тел приведены в табл. Д2. Прочерк в таблице означает, что тело отсутствует и изображать его не надо. Если масса тела равна нулю, то данное тело показывается на рисунке, но его массой при расчетах следует пренебречь.
В некоторый момент времени под действием сил тяжести система приходит в движение из состояния покоя.
При скольжении по плоскостям на грузы действуют силы трения, коэффициент трения скольжения f равен 0,01. Качение всех тел происходит без скольжения; при этом для случая качения тел по неподвижным плоскостям следует учитывать трение качения, коэффициент трения качения δ = 1 см. Трением в осях вращения пренебречь. Длины нитей и длины участков достаточны для того, чтобы тела при движении не сталкивались друг с другом.
Определить скорость, указанную в табл. Д2 в столбце «Найти», после того как этот груз переместится на расстояние s = 10 м. При этом нужно указать, в какую сторону этот груз движется.
Таблица Д2а
Исходные данные
| Номер условия 1 | ||||
| m1, кг | m2, кг | m3, кг | m4, кг | m5, кг |
| 0 | 150 | 0 | 0 | 120 |
| m6, кг | m7, кг | m8, кг | m9, кг | Найти |
| 200 | — | 90 | — | V8 |
Оформление готовой работы
ВУЗ: ИРНИТУ
Все задачи из: Теоретическая механика ИРНИТУ
11.15 ЗАДАНИЕ Д-3
На звено 1 механизма, угловая скорость которого равна ω10, с некоторого момента времени (t = 0) начинает действовать пара сил с моментом M (движущий момент) или движущая сила Р.
Массы звеньев 1 и 2 механизма равны соответственно m1 и m2, а масса поднимаемого груза 3 — m3. Момент сил сопротивления вращению ведомого звена 2 равен МC. Радиусы больших и малых окружностей звеньев 1 и 2: R1, r1, R2, r2 .
Схемы механизмов показаны на рис. 3.1-3.3, а необходимые для решения данные приведены в табл. 3.1.
Найти уравнение вращательного движения звена механизма, указанного в последней графе табл. 3.1. Определить также натяжение нитей в заданный момент времени, а в вариантах, где имеется соприкасание звеньев 1 и 2, найти окружное усилие в точке их касания. Звенья 1 и 2, для которых радиусы инерции ρ1 и ρ2 в табл. 3.1 не заданы, считать сплошными однородными дисками.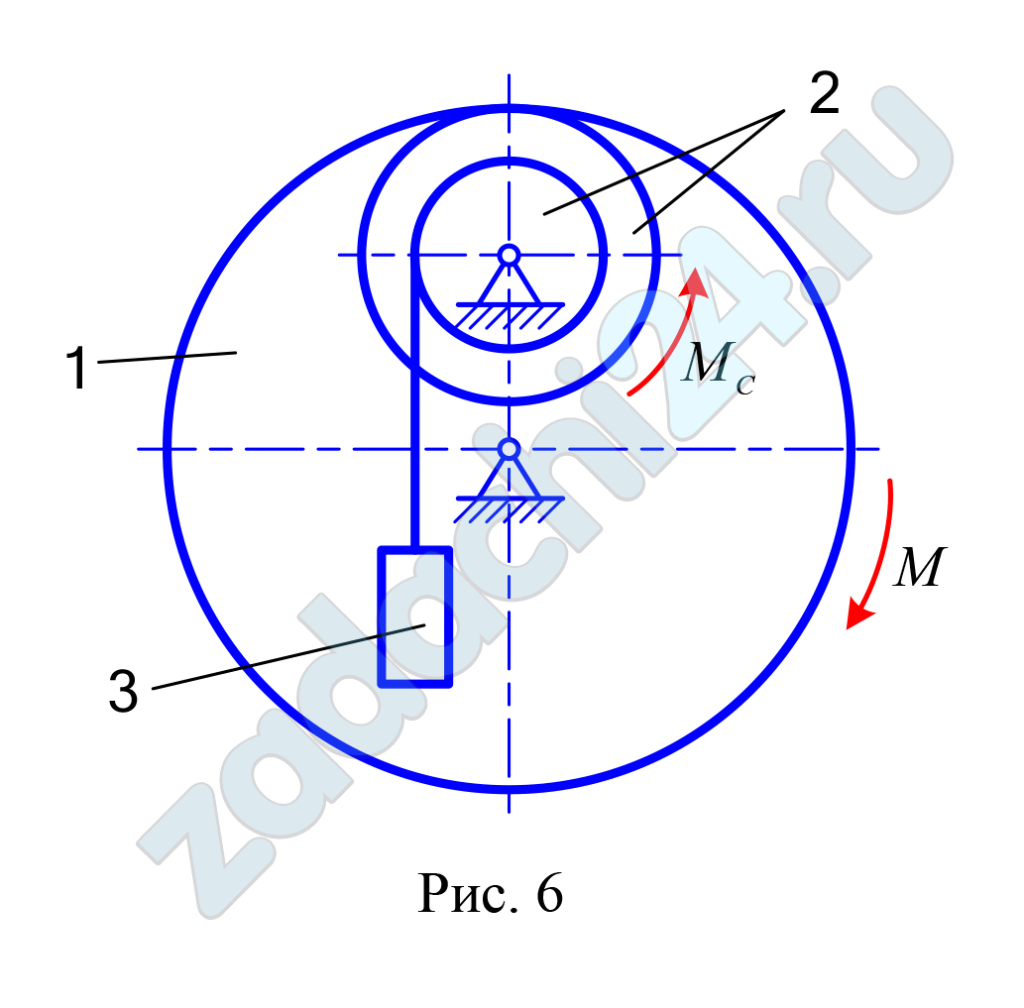
Таблица Д-3
| № варианта | m1, кг | m2, кг | m3, кг | R1, см | R2, см | r2, см |
| 6 | 400 | 250 | 600 | 70 | 30 | 20 |
Продолжение таблицы Д-3
| ρ1, см | ρ2, см | М, Н·м | МС, Н·м | ω10, с-1 | t, с | Найти |
| 70 | 20√2 | 4800+10е2t | 800 | 3 | 4 | φ1 |
Варианты: 11.
ВУЗ: Московский Политех
Все задачи из: Теоретическая механика Московский Политех
11.15.11 ЗАДАНИЕ Д-3
На звено 1 механизма, угловая скорость которого равна ω10, с некоторого момента времени (t = 0) начинает действовать пара сил с моментом M (движущий момент) или движущая сила Р.
Массы звеньев 1 и 2 механизма равны соответственно m1 и m2, а масса поднимаемого груза 3 — m3. Момент сил сопротивления вращению ведомого звена 2 равен МC. Радиусы больших и малых окружностей звеньев 1 и 2: R1, r1, R2, r2 .
Схемы механизмов показаны на рис. 3.1-3.3, а необходимые для решения данные приведены в табл. 3.1.
Найти уравнение вращательного движения звена механизма, указанного в последней графе табл. 3.1. Определить также натяжение нитей в заданный момент времени, а в вариантах, где имеется соприкасание звеньев 1 и 2, найти окружное усилие в точке их касания. Звенья 1 и 2, для которых радиусы инерции ρ1 и ρ2 в табл. 3.1 не заданы, считать сплошными однородными дисками.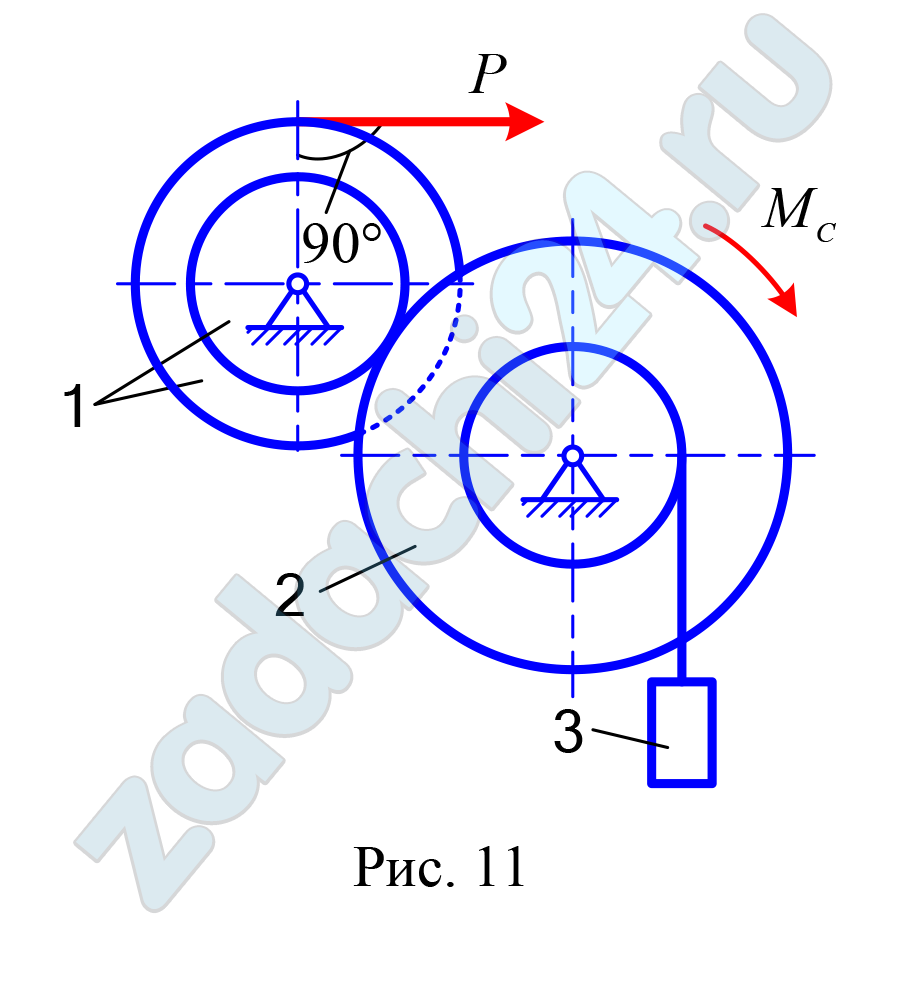
Таблица Д-3
| № варианта | m1, кг | m2, кг | m3, кг | R1, см | r1, см | R2, см | r2, см |
| 11 | 150 | 300 | 700 | 40 | 30 | 60 | 30 |
Продолжение таблицы Д-3
| ρ1, см | ρ2, см | Р, Н | МС, Н·м | ω10, с-1 | t, с | Найти |
| 30 | 40 | 3900+50t2 | 1000 | 1 | 2 | φ1 |
11.16 ЗАДАНИЕ Д-5
Теорема об изменении кинетической энергии механической системы
Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывается трение скольжения тела А и сопротивление качению тела D, катящегося без скольжения. Другими силами сопротивления и массами нерастяжимых нитей пренебрегаем. Требуется определить скорость и ускорение тела А в тот момент, когда оно пройдет путь SA = S.
В задаче обозначено:
mA, mB, mD, mE — массы тел A, B, D, E;
RB, rB, RD, rD, RE, rE — радиусы больших и малых окружностей тел B, D, E;
ρB, ρD, ρE — радиусы инерции тел В, D, Е относительно горизонтальных осей, проходящих через их центры тяжести;
α — угол наклона плоскости к горизонту;
f — коэффициент трения скольжения тела А;
k — коэффициент трения качения тела D.
Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами. Наклонные участки нитей параллельны соответствующим наклонным плоскостям.
Считать величину m равной 10 кг, g = 10 м/с².
Таблица Д-5
| № варианта | № рисунка | mА, кг | mВ, кг | mЕ, кг | mD, кг |
| 6 | 6 | 9m | 8m | 3m | 3m |
Продолжение таблицы Д-6
| RВ, м | rВ, м | ρВ, м | RD, м | rD, м | ρD, м | α,º | k, см | S, м |
| 0,8 | 0,5 | 0,7 | 0,9 | 0,3 | 0,5 | 20 | 0,4 | 1,5 |
ВУЗ: Московский Политех
Все задачи из: Теоретическая механика Московский Политех