1 Физические свойства жидкостей

1.141  Определить изменение давления в закрытом резервуаре с бензином с изменением температуры от 20 до 70 ºС.

Ответ: dp=38 МПа.

1.142 Определить изменение скорости распространения звука в жидкости при увеличении температуры с 10 до 30 ºС.

Ответ: Δс=28 м/c.

1.143 На сколько процентов увеличится начальный объем воды, спирта и нефти при увеличении температуры на 10 ºС?

Ответ: dW₁/dt=0,15 %, dW₂/dt=1,1 %, dW₃/dt=0,6 %.

1.144 Рассмотреть явление капиллярности в стеклянных пьезометрических трубках диаметрами d₁=5 мм, d₂=2 мм, d₃=10 мм для воды, спирта (рис. 1, а) и ртути (рис. 1, б).

Ответ: h_в.кап1=6 мм, h_в.кап2=15 мм, h_в.кап3=3 мм, h_рт.кап1=-2,3 мм, h_рт.кап2=-5,75 мм, h_рт.кап3=-1,15 мм, h_сп.кап1=2,03 мм, h_сп.кап2=5,08 мм, h_сп.кап3=1,02 мм.

1.145 Разность скоростей между двумя соседними слоями жидкости толщиной ðn=0,02 мм равна ðu=0,0072 м/ч. Рассматриваемая жидкость имеет коэффициент динамической вязкости μ=13,04·10^-4 Н·с/м². Определить тангенциальное напряжение и силу трения на 1 м² поверхности между слоями жидкости (рис. 1).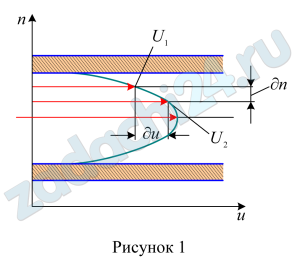

Ответ: τ=13,04·10^-5 Н/м².

1.146 Определить силу трения и тангенциальное напряжение на площади a×b=10×10 см² при температуре воды t=14 ºC и разности скоростей между двумя соседними слоями толщиной ðn=0,25 мм, равной ðu=0,0003 м/мин. Динамическая вязкость при данной температуре μ₁₄=17,92·10^-4 Н·с/см².

Ответ: Т=23,66·10^-8 Н, τ=23,66·10^-6 Н/м².

1.147  Определить кинематический коэффициент вязкости воды, если сила трения Т=12·10^-4 Н на поверхность S=0,06 м² создает скорость деформации ðu/ðn=1.

Ответ: ν=2·10^-5 м²/c.

1.148 Определить силу трения и тангенциальное напряжение на площади воды S=0,2·10^-2 м² при температуре t=8 ºС, предполагая, что скорость деформации равна единице.

Ответ: Т=27,6·10^-7 Н, τ=13,8·10^-4 Н/м².

1.149 Определить величину деформации сплошной среды для интервала ðτ=0,1 с, если вода имеет температуру 9 ºС и соответствующее тангенциальное напряжение τ=28·10^-4 Н/м² (рис. 1).

Ответ: ðβ=0,2.